
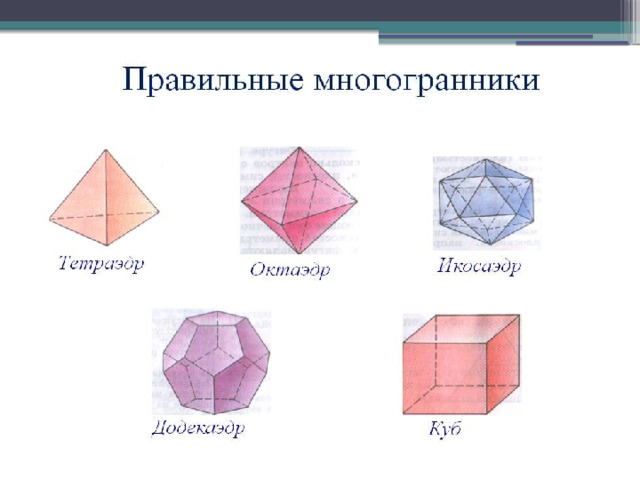
Тема урока: «Правильные многогранники»
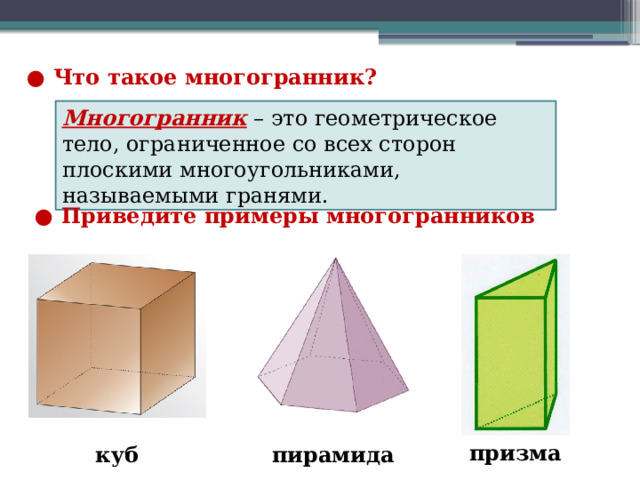
● Что такое многогранник?
Многогранник – это геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями.
● Приведите примеры многогранников
призма
куб
пирамида
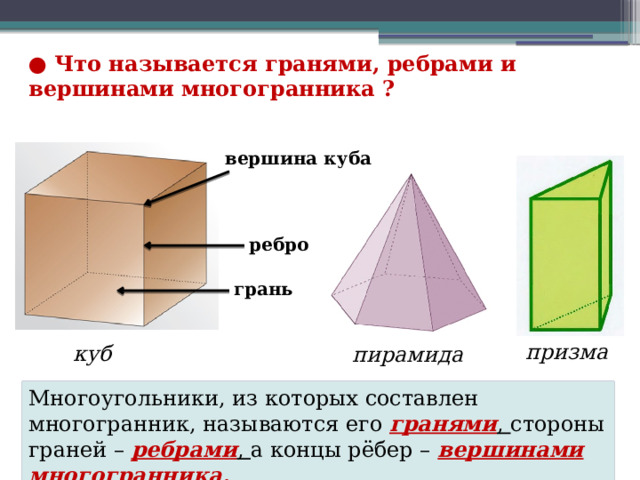
● Что называется гранями, ребрами и вершинами многогранника ?
вершина куба
ребро
грань
призма
куб
пирамида
Многоугольники, из которых составлен многогранник, называются его гранями , стороны граней – ребрами , а концы рёбер – вершинами многогранника.
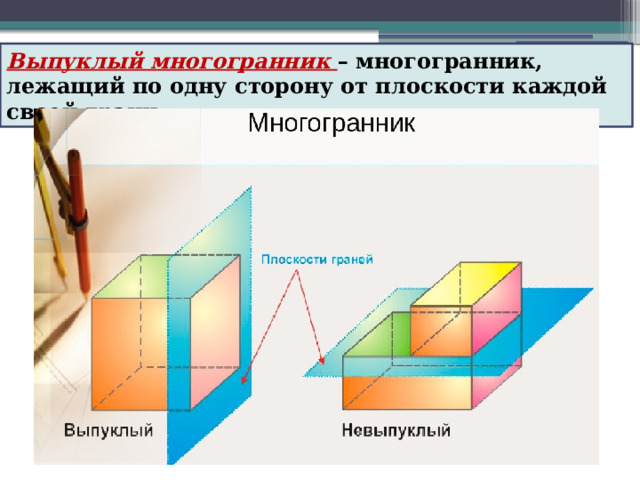
Выпуклый многогранник – многогранник, лежащий по одну сторону от плоскости каждой своей грани.

Какие из приведенных ниже многогранников являются выпуклыми ?
Выпуклый многогранник – многогранник, лежащий по одну сторону от плоскости каждой своей грани.
призма
параллелепипед
тетраэдр
Невыпуклые многогранники
Выпуклые многогранники
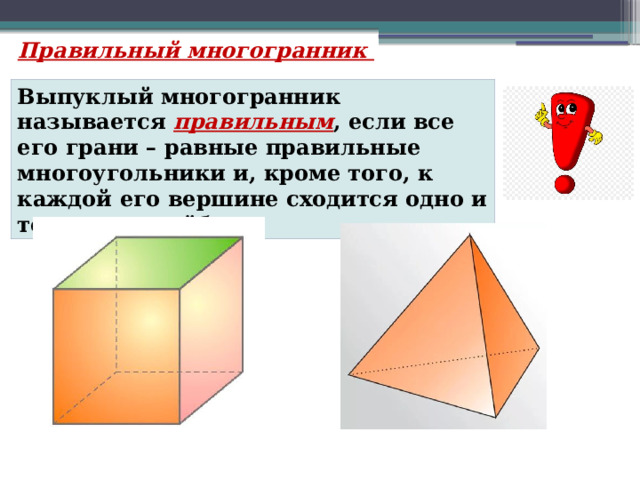
Правильный многогранник
Выпуклый многогранник называется правильным , если все его грани – равные правильные многоугольники и, кроме того, к каждой его вершине сходится одно и тоже число рёбер.
![Правильный тетраэдр Тетраэдр – от греческих [тетра] – четыре и [эдра] – основание, грань ● правильный тетраэдр составлен из _______ равносторонних треугольников; ● каждая его вершина является вершиной _______треугольников. четырёх трёх Посчитай! 4 Вершины – Ребра – Грани - 6 4](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img7.jpg)
Правильный тетраэдр
Тетраэдр – от греческих [тетра] – четыре и [эдра] – основание, грань
● правильный тетраэдр составлен из _______ равносторонних треугольников;
● каждая его вершина является вершиной _______треугольников.
четырёх
трёх
Посчитай!
4
Вершины –
Ребра –
Грани -
6
4
![Правильный октаэдр Октаэдр – от греческого [окто] – восемь ● правильный октаэдр составлен из _________ равносторонних треугольников ; ● каждая его вершина является вершиной _______ треугольников; восьми четырёх Посчитай! Вершины – Ребра – Грани - 6 12 8](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img8.jpg)
Правильный октаэдр
Октаэдр – от греческого [окто] – восемь
● правильный октаэдр составлен из _________ равносторонних треугольников ;
● каждая его вершина является вершиной _______ треугольников;
восьми
четырёх
Посчитай!
Вершины –
Ребра –
Грани -
6
12
8
![Правильный икосаэдр Икосаэдр – от греческого [эйкоси] – двадцать ♦ правильный икосаэдр составлен из __________ равносторонних треугольников; ♦ каждая его вершина является вершиной ______ треугольников; двадцати пяти Посчитай! 12 Вершины – Ребра – Грани - 30 20](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img9.jpg)
Правильный икосаэдр
Икосаэдр – от греческого [эйкоси] – двадцать
♦ правильный икосаэдр составлен из __________ равносторонних треугольников;
♦ каждая его вершина является вершиной ______ треугольников;
двадцати
пяти
Посчитай!
12
Вершины –
Ребра –
Грани -
30
20
![Куб Гексаэдр или куб – от греческого [гекса] – шесть ♦ куб составлен из ______ квадратов; шести ♦ каждая его вершина является вершиной ______квадратов. трёх Посчитай! 8 Вершины – Ребра – Грани - 12 6](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img10.jpg)
Куб
Гексаэдр или куб – от греческого [гекса] – шесть
♦ куб составлен из ______ квадратов;
шести
♦ каждая его вершина является вершиной ______квадратов.
трёх
Посчитай!
8
Вершины –
Ребра –
Грани -
12
6
![Правильный додекаэдр Додекаэдр – от греческого [додека] – двенадцать ♦ правильный додекаэдр составлен из ___________ правильных пятиугольников; ♦ Каждая его вершина является вершиной ______ правильных пятиугольников. двенадцати трёх Посчитай! Вершины – Ребра – Грани - 20 30 12](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img11.jpg)
Правильный додекаэдр
Додекаэдр – от греческого [додека] – двенадцать
♦ правильный додекаэдр составлен из ___________ правильных пятиугольников;
♦ Каждая его вершина является вершиной ______ правильных пятиугольников.
двенадцати
трёх
Посчитай!
Вершины –
Ребра –
Грани -
20
30
12


Из истории многогранников
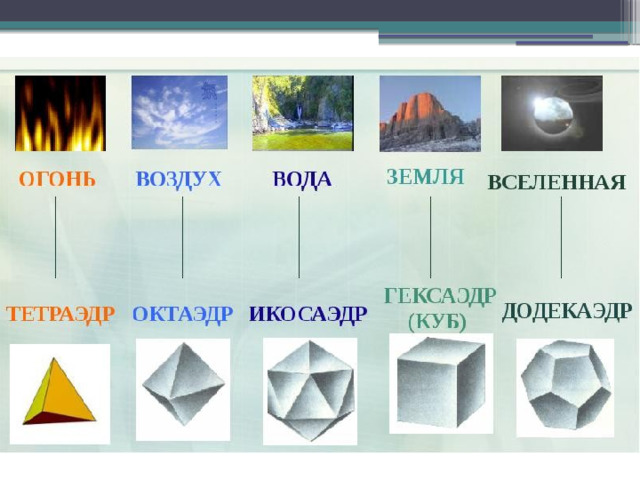
Значительное внимание правильным многогранникам уделял древнегреческий философ Платон (около 429 – 347 г. г. до н. э), в честь которого они и названы «Платоновы тела». Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Каждой из четырёх стихий он сопоставил определённый правильный многогранник.
Платон
Пифагор

Полное математическое описание пяти правильных многогранников дал древнегреческий математик Евклид (около 365 – 300 г. г. до н.э.) и доказал, что других правильных многогранников нет.
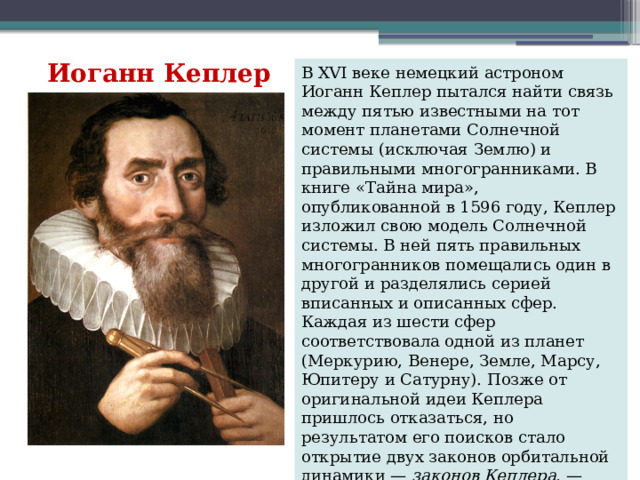
Иоганн Кеплер
В XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы (исключая Землю) и правильными многогранниками. В книге «Тайна мира», опубликованной в 1596 году, Кеплер изложил свою модель Солнечной системы. В ней пять правильных многогранников помещались один в другой и разделялись серией вписанных и описанных сфер. Каждая из шести сфер соответствовала одной из планет (Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну). Позже от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики — законов Кеплера , — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников (тел Кеплера — Пуансо).
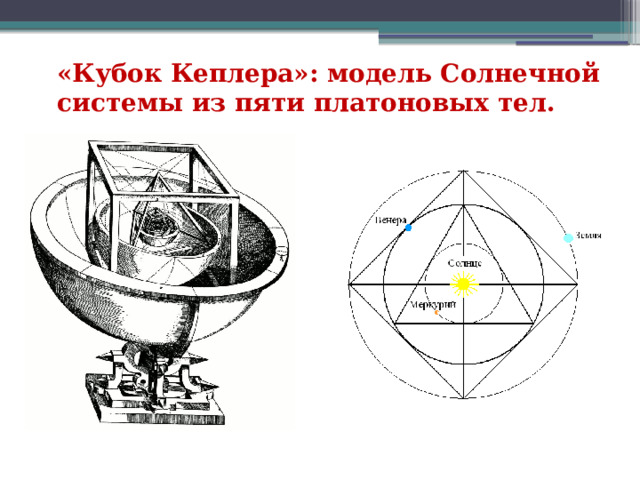
«Кубок Кеплера»: модель Солнечной системы из пяти платоновых тел.

Многогранники вокруг нас
кристаллы поваренной соли

Многогранники вокруг нас
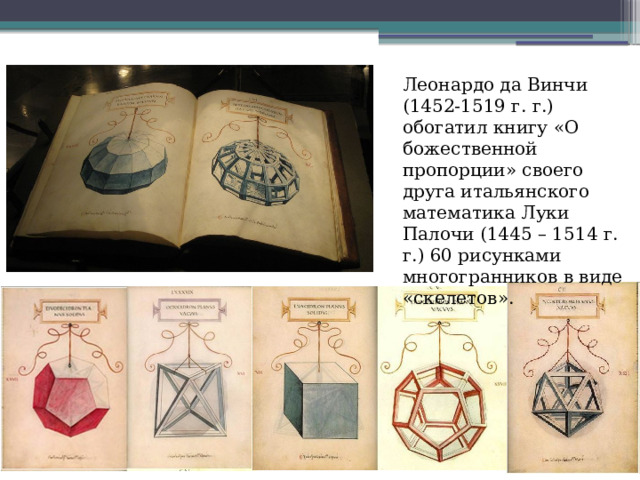
Леонардо да Винчи (1452-1519 г. г.) обогатил книгу «О божественной пропорции» своего друга итальянского математика Луки Палочи (1445 – 1514 г. г.) 60 рисунками многогранников в виде «скелетов».

Тайная вечеря (картина Сальвадора Дали)


Спасибо за внимание!















![Правильный тетраэдр Тетраэдр – от греческих [тетра] – четыре и [эдра] – основание, грань ● правильный тетраэдр составлен из _______ равносторонних треугольников; ● каждая его вершина является вершиной _______треугольников. четырёх трёх Посчитай! 4 Вершины – Ребра – Грани - 6 4](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img7.jpg)
![Правильный октаэдр Октаэдр – от греческого [окто] – восемь ● правильный октаэдр составлен из _________ равносторонних треугольников ; ● каждая его вершина является вершиной _______ треугольников; восьми четырёх Посчитай! Вершины – Ребра – Грани - 6 12 8](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img8.jpg)
![Правильный икосаэдр Икосаэдр – от греческого [эйкоси] – двадцать ♦ правильный икосаэдр составлен из __________ равносторонних треугольников; ♦ каждая его вершина является вершиной ______ треугольников; двадцати пяти Посчитай! 12 Вершины – Ребра – Грани - 30 20](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img9.jpg)
![Куб Гексаэдр или куб – от греческого [гекса] – шесть ♦ куб составлен из ______ квадратов; шести ♦ каждая его вершина является вершиной ______квадратов. трёх Посчитай! 8 Вершины – Ребра – Грани - 12 6](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img10.jpg)
![Правильный додекаэдр Додекаэдр – от греческого [додека] – двенадцать ♦ правильный додекаэдр составлен из ___________ правильных пятиугольников; ♦ Каждая его вершина является вершиной ______ правильных пятиугольников. двенадцати трёх Посчитай! Вершины – Ребра – Грани - 20 30 12](https://fsd.multiurok.ru/html/2024/02/20/s_65d505359bae6/img11.jpg)






























