Россия, Кантемировка
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Был в сети 23.12.2022 10:40
Голубченко Юрий Яковлевич
Учитель физики и математики
74 года
1 421
43 763 
Местоположение
Специализация
Презентация " Решение неравенств с одной переменной"
Категория:
Алгебра
06.11.2022 20:46
Просмотр содержимого документа
«Презентация " Решение неравенств с одной переменной"»
Тема урока: Решение неравенств
с одной переменной
8 класс
b, ax научиться решать неравенства с одной переменной, опираясь на свойства равносильности. " width="640"
Цели урока
- ввести понятия «решение неравенства», «равносильные неравенства»;
- познакомиться со свойствами равносильности неравенств;
- рассмотреть решение линейных неравенств вида ах b, ax
- научиться решать неравенства с одной переменной, опираясь на свойства
равносильности.
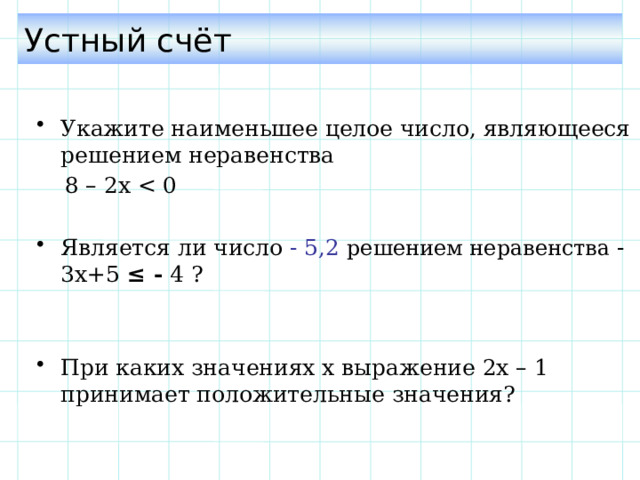
Устный счёт
- Укажите наименьшее целое число, являющееся решением неравенства
8 – 2х
- Является ли число - 5,2 решением неравенства -3х+5 ≤ - 4 ?
- При каких значениях х выражение 2х – 1 принимает положительные значения?
-2 4. k ≤ -2,1 -2 -2,1 Ответ: (-∞;-2] Ответ: (-∞; -2,1) 9 " width="640"
Устный счет - Найди ошибку
1. Х
5,5
Ответ: (-∞;9 ] Ответ: [-∞;5,5]
3 . n -2 4. k ≤ -2,1
-2 -2,1
Ответ: (-∞;-2] Ответ: (-∞; -2,1)
9
Устный счет
«Читаем промежутки»
Используем триггер, что позволяет учащимся определить последовательность решения примеров. Нажмите на голубой прямоугольник – появится соответствующий правильный ответ.
4
Устный счет
Какие промежутки соответствуют
геометрическим моделям:
х
8
3
х
-1,5
2,5
х
5
Используем триггер, что позволяет учащимся определить последовательность решения примеров. Нажмите на числовой луч – появится соответствующий правильный ответ.
х
-4
6
3 при х = 4 5 • 4 – 11 3; 9 3 – верно; при х = 2 5 • 2 – 11 3, - 1 3 – неверно; Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство. " width="640"
Рассмотрим неравенство 5х – 11 3
- при х = 4 5 • 4 – 11 3; 9 3 – верно;
- при х = 2 5 • 2 – 11 3, - 1 3 – неверно;
Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
0 и равносильны х 3 х 2 + 4 ≤ 0 и |х| + 3 нет решений 3х – 6 ≥ 0 и 2х 8 неравносильны х ≥ 2 х 4 " width="640"
Равносильные неравенства
Неравенства, имеющие одни и те же решения, называют равносильными. Неравенства, не имеющие решений, тоже считают равносильными
2х – 6 0 и равносильны х 3
х 2 + 4 ≤ 0 и |х| + 3 нет решений
3х – 6 ≥ 0 и 2х 8 неравносильны
х ≥ 2 х 4
При решении неравенств используются следующие свойства :
- Если из одной части неравенства перенести в другую слагаемое с противоположным знаком , то получится равносильное ему неравенство.
- Если обе части неравенства умножить или разделить на одно и то же положительное число , то получится равносильное ему неравенство;
- если обе части неравенства умножить или разделить на одно и то же отрицательное число , изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Решаем неравенства .
Все действия на слайде – последовательно щелчком мышки.
х
-3
Ответ:
10
Решаем неравенства .
Покажите решение на числовой прямой и запишите ответ в виде интервала:
Используем триггер, что позволяет учащимся определить последовательность решения примеров. Нажмите на голубой прямоугольник – появится соответствующий правильный ответ.
10
Решаем неравенства.
Запишите ответ в виде интервала:
Используем триггер, что позволяет учащимся определить последовательность решения примеров. Нажмите на голубой прямоугольник – появится соответствующий правильный ответ.
10
Алгоритм решения неравенств первой степени с одной переменной.
- Раскрыть скобки и привести подобные слагаемые.
- Сгруппировать слагаемые с переменной в левой части неравенства, а без переменной – в правой части, при переносе меняя знаки.
- Привести подобные слагаемые.
- Разделить обе части неравенства на коэффициент при переменной, если он не равен нулю.
- Изобразить множество решений неравенства на координатной прямой.
- Записать ответ в виде числового промежутка.
Решаем неравенства.
Запишите ответ в виде неравенства:
Используем триггер, что позволяет учащимся определить последовательность решения примеров. Нажмите на голубой прямоугольник – появится соответствующий правильный ответ.
10
Итог урока. Домашнее задание
- Выучить правила решения неравенств
- № 844 (б, в)
- № 845
Рефлексия
Мне всё понятно, у меня всё получается!
У меня ещё есть ошибки, но я стараюсь!
Я ничего не понимаю,
у меня ничего не получается!
Спасибо за внимание!
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
