Презентация "Теорема Виета"

• Какое уравнение называется квадратным?

• Какие виды квадратных уравнений вы знаете?

• Какое уравнение называется неполным квадратным?

• Какое уравнение называется приведенным?

• Что значит - решить уравнение?

• Сколько корней может иметь квадратное уравнение?

• От чего зависит количество корней квадратного уравнения?

• Какое выражение называют дискриминантом?

• Укажите в квадратном уравнении его коэффициенты

• 3у ² -5у+1=0,
• 12х-7х ² +4=0
• -х ² +х-3=0,
• Х ² -7=0.

• Сколько корней имеет квадратное уравнение ?

• Х ² -64=0,
• У ² +49=0,
• 2р ² -7р=0,
• Х ² =0

• Замените уравнение равносильным ему приведенным уравнением.

• 3х ² - 6х-12=0,
• 2у ² + у-7=0
• 0,5х ² - 3х +1,5=0.

Из предложенных уравнений

выберите приведенные квадратные уравнения

х ² - 5х + 3 = 0

5х ² = 0

х ² - 5х +6 = 0

16 - х ² - 15 = 0

8х ² - 4 +х ² = 0

67х ² - 95х = 0

х ² + 6х + 8 = 0

х ² - 34х+289 = 0

12х ² +7х= - 7х ² - 2х

10х ² - 5 = 3х ² -5

- 5х ² = 9х -2

6х ² + 7х = 5

6 - 8х ² =2х+9

-16 + х ² = 0

Решить оставшиеся уравнения

Будущий преобразователь алгебры Франсуа Виет (1504 – 1603) появился на свет в маленьком французском городке. В 1560 году он окончил парижский университет и начал адвокатскую практику, через несколько лет перешел на государственную службу, став сначала советником короля Генриха ΙΙΙ, а затем рекетмейстером – докладчиком по ходатайствам.

В 1569 году покровитель Виета – король – был убит, и Виет стал служить новому королю. Жизнь его проходила на фоне кровавых событий войны, которую вели две мощные религиозные группировки католиков и протестантов – гугенотов. Достаточно сказать, что он пережил Варфоломеевскую ночь.

Но был небольшой промежуток времени, когда из-за происков врагов Виет был отстранен от военной службы и получил неожиданный досуг.

Сейчас нам трудно представить математику без формул и уравнений, но именно такой была она для Виета. Виет завершил создание буквенного исчисления, введя обозначения не только для неизвестного и его степени, но и для параметров. Это позволило записать целые классы задач, которые можно решать с помощью одного правила. Он встал у истоков создания новой науки – тригонометрии. Многие тригонометрические формулы, которые ныне изучают в курсе математики средней школы, впервые были записаны Виетом. В 1593 году он первым сформулировал теорему косинусов. Четыре года опалы оказались необычайно плодотворными для Виета. Он работал самозабвенно. По рассказам современников Виет

мог просиживать за письменным столом по трое

суток подряд. Только иногда забываясь сном на

несколько минут. В тот период он начал большой

труд, который назвал «Искусство анализа, или

Новая алгебра». Книгу он не завершил, но главное,

что определило развитие всей математики Нового

времени, было написано.

Квадратное уравнение, у которого первый коэффициент равен 1, называется приведенным квадратным уравнением .

х 2 + px + q = 0

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

х 1 + х 2 = - р

х 1 · х 2 = q

Теорема Виета замечательна тем, что, не зная корней квадратного трехчлена, мы легко можем вычислить их сумму и произведение, то есть простейшие симметричные выражения x 1 + x 2 и x 1 · x 2 . Так, еще не зная, как вычислить корни уравнения x ² – x – 1 = 0, мы, тем не менее, можем сказать, что их сумма должна быть равна 1, а произведение должно равняться –1.

Теорема Виета позволяет угадывать целые корни квадратного трехчлена. Так, находя корни квадратного уравнения x ² – 5x + 6 = 0, можно начать с того, чтобы попытаться разложить свободный член (число 6) на два множителя так, чтобы их сумма равнялась бы числу 5. Это разложение очевидно: 6 = 2 * 3 ; 2 + 3 = 5.

Отсюда должно следовать,

что числа 2 и 3 являются искомыми корнями.

Если в квадратном уравнении ах² + вх + с = 0 выполняется равенство а + с = в, то х 1 = -1; х 2 = - с/а

Свойства коэффициентов квадратного уравнения

Если в квадратном уравнении ах² + вх + с = 0 сумма коэффициентов а + в + с = 0, то х 1 = 1; х 2 = с/а

Пример. 5х² - 8х +3 = 0

так как 5 – 8 + 3 = 0, то х 1 = 1; х 2 = 0,6

.

.

.

Пример. 5х² + 8х +3 = 0

так как 5 + 3 = 8, то Х 1 = - 1; Х 2 = - 0,6

Х 1 + Х 2 = - р ; Х 1 · Х 2 = q

Теорема Виета. Нет формулы важней.

Для приведенного уравнения

Р – это сумма корней,

q – его корень произведения .

Пример 1:

• Приведенное уравнение x ² – 7x + 10 = 0 имеет корни 2 и 5.
• Сумма корней равна 7, а произведение равно 10.
• В нашем уравнении второй коэффициент равен -7,

а свободный член 10.

• Таким образом, сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней – свободному члену.

Пример 2.

• Решить квадратное уравнение х ² – 2х – 24 = 0.

• Решение.

• Применяем теорему Виета и записываем два тождества:
• Х 1 · Х 2 = –24
• Х 1 + Х 2 = 2
• Подбираем такие множители для –24, чтобы их сумма была равна 2. После недолгих размышлений находим: 6 и –4.

• Проверим:

• 6 · (– 4) = –24.
• 6 + (– 4) = 6 – 4 = 2.

Решите уравнение : 5x ² − 35x + 50 = 0.

• Перед нами уравнение, которое не является приведенным, т.к. коэффициент a = 5. Разделим все на 5, получим: x ² − 7x + 10 = 0.
• Все коэффициенты квадратного уравнения целочисленные — попробуем решить по теореме Виета. Имеем: x 1 + x 2 = −(−7) = 7; x 1 · x 2 = 10.
• В данном случае корни угадываются легко — это 2 и 5. Считать через дискриминант не надо.

• По праву достойна в стихах быть воспета
• О свойстве корней Теорема Виета.
• Что лучше, скажи, постоянства такого?
• Умножишь ты корни и дробь уж готова
• В числителе “С”, в знаменателе “А”.
• А сумма корней тоже дроби равна
• Хоть с минусом дробь – это что за беда?
• В числителе “В”, в знаменателе “А”.

Задание 1. У какого из заданных квадратных уравнений сумма корней равна -6, а произведение равно -11

• х² - 6х + 11 = 0
• х² + 6х - 11 = 0

• х² + 6х + 11 = 0

• х² - 11х - 6 = 0

• х² + 11х - 6 = 0

Задание 2. ) Если х1 = -5 и х2 = -1 - корни уравнения х² + px +q = 0, то

1) p = -6, q = -5

2) p = 5, q = 6

3) p = 6, q = 5

4) p = -5, q = -6

5) p = 5, q = -6

6) p = -6, q = -5

Задание 3. Сумма и произведение корней уравнения х² - 3х - 5 = 0 равны

• х 1 + х 2 = -3, х 1 ∙ х 2 = -5

• х 1 + х 2 = -5, х 1 ∙ х 1 = -3
• х 1 + х 2 = 3, х 1 ∙ х 2 = -5
• х 1 + х 2 = 5, х 1 ∙ х 2 = -3

Устная работа

• У какого из данных квадратных уравнений сумма корней равна -6 , а произведение -11

• 1. x² - 6 x +11 =0
• 2. x² +6 x - 11 =0
• 3. x² +6 x +11 =0
• 4. x² - 11 x - 6 =0
• 5. x² +11 x - 6 =0

• Если х=-5 и х=-1 корни приведенного квадратного уравнения x²+px+q=0 ?

• 1 . р=-6 q=-5

• 2. p=5 q=6
• 3. p=6 q=5
• 4. p=-5 q =-6
• 5. p=6 q=5

Определите знаки корней данного уравнения

x²+4x-12=0

• Решите квадратное уравнение:

• x ² − 9x + 14 = 0;

• x ² − 12x + 27 = 0;

• 3x ² + 33x + 30 = 0;

• − 7x ² + 77x − 210 = 0.

• x ² − 9x + 14 = 0 — это приведенное квадратное уравнение.

• По теореме Виета имеем: Х 1 + Х 2 = −(−9) = 9; Х 1 ·Х 2 = 14.

Корни — числа 2 и 7;

• x ² − 12x + 27 = 0 — тоже приведенное.

По теореме Виета: Х 1 + Х 2 = −(−12) = 12; Х 1 ·Х 2 = 27. Корни: 3 и 9;

• 3x ² + 33x + 30 = 0 — это уравнение не является приведенным. Разделим обе стороны уравнения на коэффициент a = 3. Получим:

x ² + 11x + 10 = 0.

• По теореме Виета: Х 1 + Х 2 = −11; Х 1 ·Х 2 = 10 ⇒ корни: −10 и −1;

• − 7x ² + 77x − 210 = 0 — коэффициент при x ² не равен 1, т.е. уравнение не приведенное. Делим все на число a = −7.

• Получим: x ² − 11x + 30 = 0.
• По теореме Виета: Х 1 + Х 2 = −(−11) = 11; Х 1 ·Х 2 = 30; ⇒

корни: 5 и 6.

Евклид (3 в. до н.э.)

Древнегреческий математик, работал в Александрии. Главный труд «Начала»(15 книг), содержит основы античной математики, элементарной геометрии, теории чисел, общей теории отношений и метода определения площадей и объемов, включавшего элементы теории пределов, оказал огромное влияние на развитие математики.

Диофант Александрийский (около 3 в.).

Диофант - древнегреческий математик из Александрии (возможно, что он был эллинизированный вавилонянин). Мы очень мало знаем о нем. Автор трактата Арифметика в 13 книгах(сохранились 6 книг) посвященного главным образом исследованию неопределенных уравнений (т.н. диофантовых уравнений). Одним из первых Диофант стал использовать при записи алгебраических рассуждений специальные знаки. На результаты, полученные Диофантом, впоследствии опирались Ферма, Эйлер, Гаусс и др.

0. В данном уравнении коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим. " width="640"

Брахмагупта

(около 598 – 660 г. г.)

Последний и наиболее выдающийся из древних индийских математиков и астрономов. Родом из Удджайна в Средней Индии,

где у него была астрономическая обсерватория. В 628 г. изложил четвертую индуистскую астрономическую систему в стихотворной форме в сочинении Открытие Вселенной (Брахма-спхута-сиддханта). Две его главы посвящены математике, в том числе арифметической прогрессии и доказательству различных геометрических теорем. Остальные 23 главы посвящены астрономии: в них описаны фазы Луны, соединения планет, солнечные и лунные затмения, даны расчеты положений планет. Труд Брахмагупты был переведен на арабский язык и таким образом попал в Египет, а оттуда в Европу. Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к форме ах 2 + b х = с, а 0. В данном уравнении коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

Аль - Хорезми

Мухаммад ибн Муса Хорезми (ок. 783 – ок. 850) – великий персидский математик, астроном и географ, основатель классической алгебры. Сведений о жизни ученого сохранилось крайне мало. Значительный период своей жизни он провел в Багдаде, возглавляя при халифе аль-Мамуне (сыне знаменитого Гаруна аль-Рашида) библиотеку «Дома мудрости». Согдиец Мухаммед ибн Муса аль-Хорезми (то есть, родом из Хорезма - с берегов Сыр-Дарьи) работал в первой половине 9 века. Главная книга Хорезми названа скромно: "Учение о переносах и сокращениях", то есть техника решения алгебраических уравнений. По-арабски это звучит «Китаб аль-джебр валь-мукабала"; отсюда произошло наше слово "алгебра".

Другое известное слово - "алгоритм", то есть четкое правило решения задач определенного типа - произошло от прозвания "аль-Хорезми". Третий известный термин, введенный в математику знаменитым согдийцем - это "синус".

Памятник

аль-Хорезми в Тегеранском университете.

В алгебраическом трактате аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

• «Квадраты равны корням», т. е. ах 2 = bх.
• «Квадраты равны числу», т. е. ах 2 = с.
• «Корни равны числу», т. е. ах = с.
• «Квадраты и числа равны корням», т. е. ах 2 + с = bх.
• «Квадраты и корни равны числу», т. е. ах 2 + bх =с.
• «Корни и числа равны квадратам», т. е. bх + с = ах 2 .
• Для аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами аль-джабр и валь-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Если числа m и п таковы,…

… что их сумма равна –р , а произведение

равно q , то эти числа являются корнями

уравнения х 2 + рх+ q = 0

Справедливо ли это утверждение?

Обратная теорема Виета

• Если два числа в сумме дают -р , а в произведении q , то эти числа являются корнями приведённого квадратного уравнения х 2 +рх+ q =0 .

• С помощью теоремы, обратной теореме Виета, можно подбором найти корни квадратного уравнения .

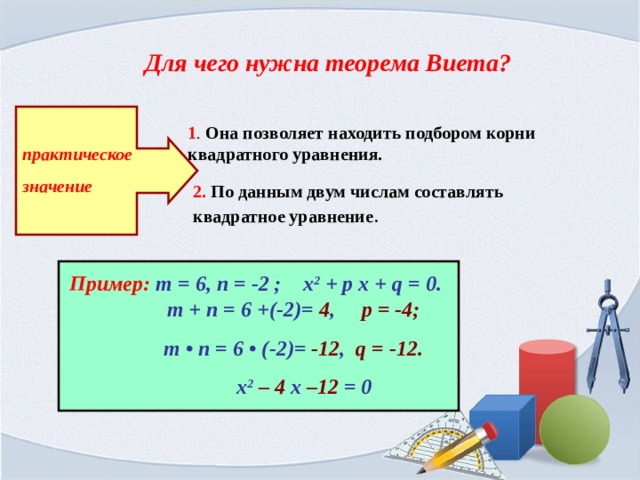
Для чего нужна теорема Виета?

1 . Она позволяет находить подбором корни квадратного уравнения.

практическое

значение

2. По данным двум числам составлять квадратное уравнение .

Пример: т = 6, п = -2 ; х 2 + р х + q = 0. т + п = 6 +(-2)= 4 , р = -4;

т • п = 6 • (-2)= -12 , q = -12.

х 2 – 4 х –12 = 0

Проверь!

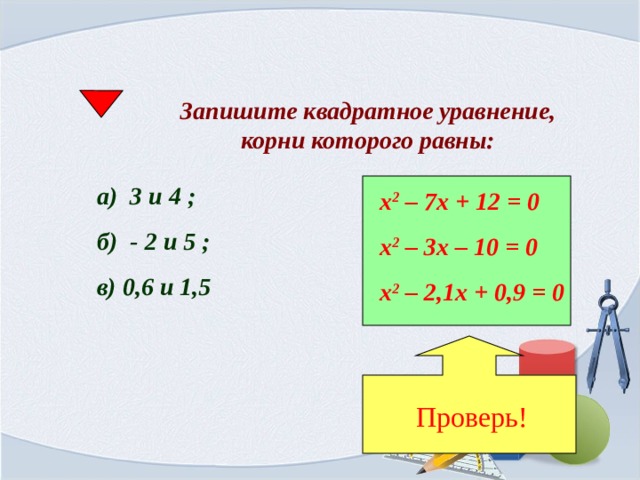
Запишите квадратное уравнение, корни которого равны:

а) 3 и 4 ;

б) - 2 и 5 ;

в) 0,6 и 1,5

х 2 – 7х + 12 = 0

х 2 – 3х – 10 = 0

х 2 – 2,1х + 0,9 = 0

Решить уравнение:

Решить самостоятельно

Работа с учебником

• № 715, 717, 719, 721, 722

Домашнее задание

Читать § 21, выполнить № 716, 718, 720, 723 ;

подготовиться к контрольной работе