Презентация тетраэдр

«Скажы мне – і я забуду. Пакажы мне – і я запомню. Уцягні мяне – і я навучуся.»

Старажытняя кітайская пагаворка

Матэматычны дыктант

• Ці праўдзіва,што калі дзве прамыя, якія перасякаюцца і ляжаць у адной плоскасці адпаведна паралельны дзвюм прамым другой плоскасці,то гэтыя плоскасці паралельны?

праўдзіва

• Ці правільнае сцвярджэнне: калі дзве прамыя не маюць агульных пунктаў ,то яны паралельныя?

не

• Хорда акружнасці належыць плоскасці.

Ці правільна, што і ўся акружнасць ляжыць у гэтай плоскасці?

не

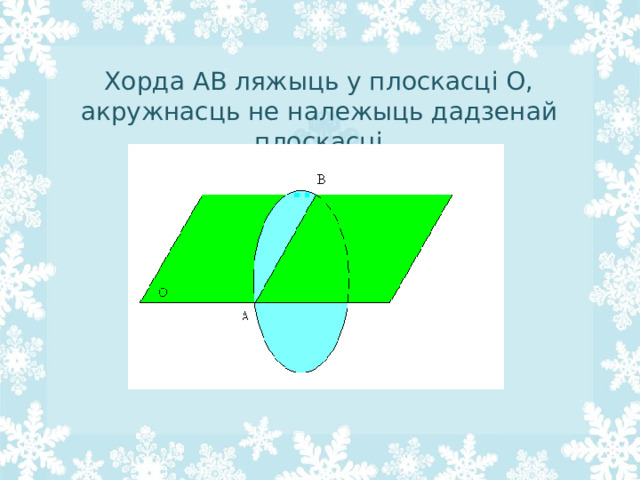
Хорда АВ ляжыць у плоскасці О, акружнасць не належыць дадзенай плоскасці

• Дзве прямые паралельны адной плоскасці. Ці можна сцвярджаць, што гэтыя прамыя паралельныя?

не

• Прамая перасякае плоскасць.

Ці можна ў плоскасці правесці прамую, паралельную дадзенай прамой?

не

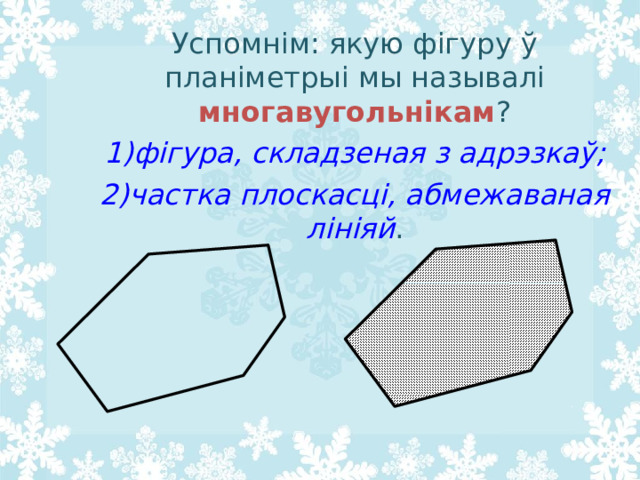
Успомнім: якую фігуру ў планіметрыі мы называлі многавугольнікам ?

• фігура, складзеная з адрэзкаў;
• частка плоскасці, абмежаваная лініяй .

D

A

B

C

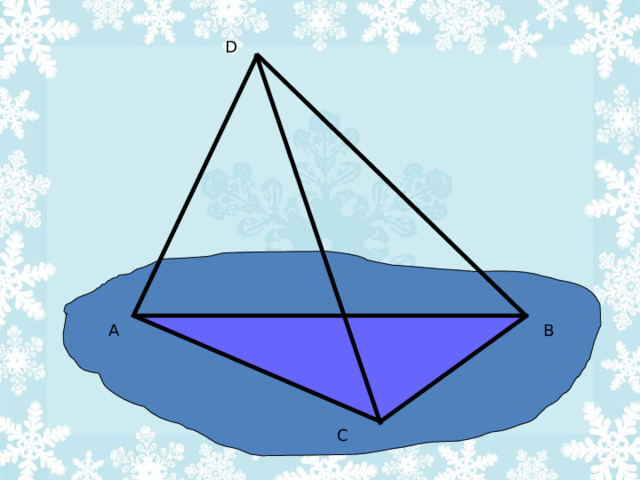
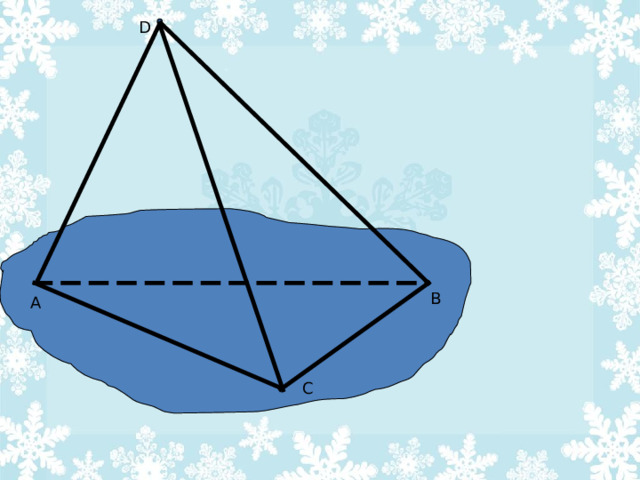
Назва гэтага мнагаграніка прыйшла з Старажытняй Грэцыі, ў ім называецца лік граняў:

«тэтра» - 4

«эдра» - грань

D

B

A

C

Платон (к аля. 428 – . 348 да н.э.)

Правільныя мнагаграннікі яшчэ называюць платонавымі цяламі, паколькі яны займаюць важкае месца ў філасоўскай карціне свету, распрацаванай вялікім мысліцелем Старажытняй Грэцыі Платонам

Платонавы целы

Гексаэдр Тэтраэдр Актаэдр Ікасаэдр Дадэкаэдр

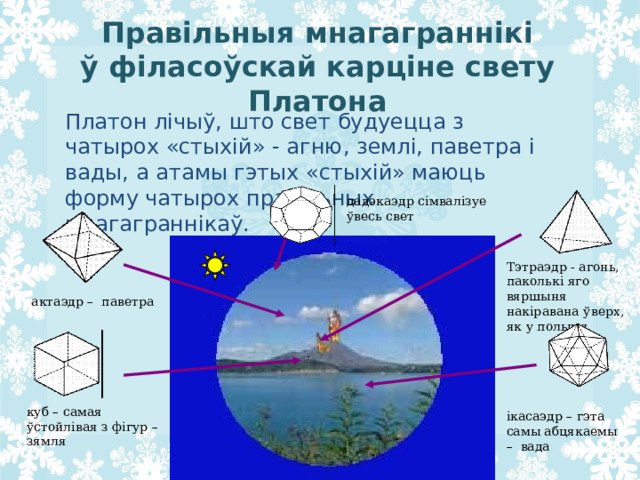
Правільныя мнагаграннікі ў філасоўскай карціне свету Платона

Платон лічыў, што свет будуецца з чатырох «стыхій» - агню, землі, паветра і вады, а атамы гэтых «стыхій» маюць форму чатырох правільных мнагаграннікаў.

дадэкаэдр сімвалізуе ўвесь свет

Тэтраэдр - агонь, паколькі яго вяршыня накіравана ўверх, як у полымя

актаэдр – паветра

куб – самая ўстойлівая з фігур – зямля

ікасаэдр – гэта самы абцякаемы – вада

Малекула метана СН4 мае форму правільнага тэтраэдра. Гэты факт падцвярджаюць здымкі молекулы метана, атрыманыя пры дапамозе электроннага мікраскопа.

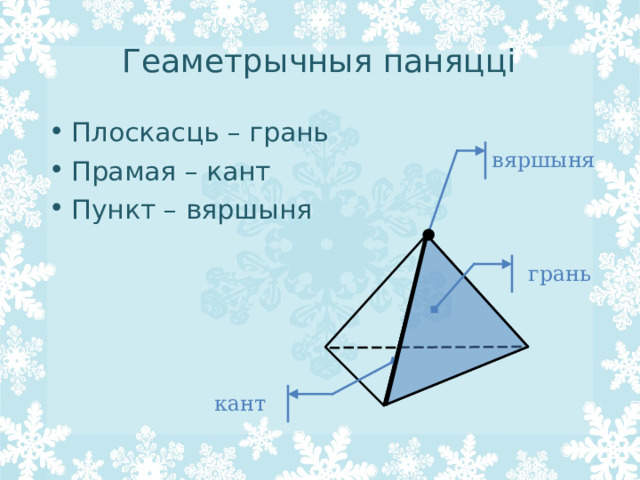
Геаметрычныя паняцці

• Плоскасць – грань
• Прамая – кант
• Пункт – вяршыня

вяршыня

грань

кант

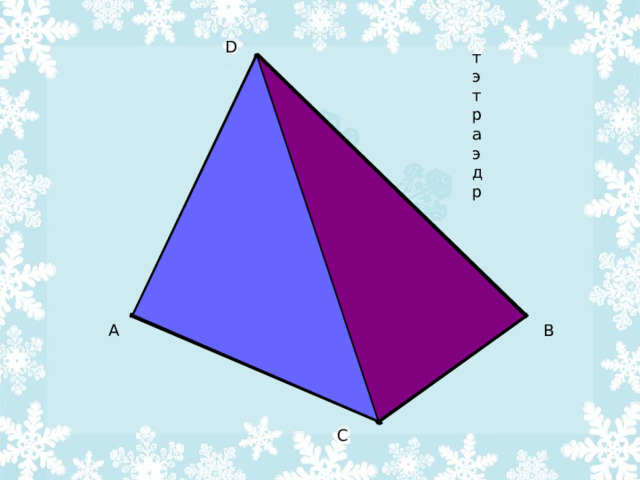
D

тэтраэдр

A

B

C

D

A

B

C

D

A

B

C

D

A

B

C

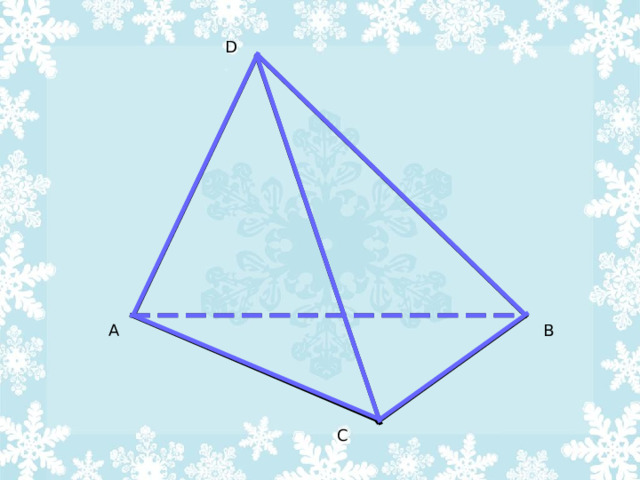
ТЭТРАЭДР. СЯЧЕННЕ ТЭТРАЭДРА.

Азначэнне тэтраэдра:

Цела, складзенае з чатырох трохвугольн і каў, называецца тэтраэдрам.

Тэтраэдр мае:

Граней-4;

Кантаў-6;

Вяршынь-6.

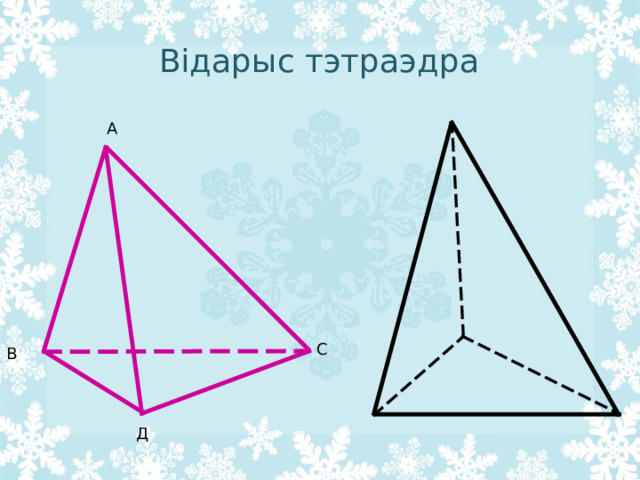
Відарыс тэтраэдра

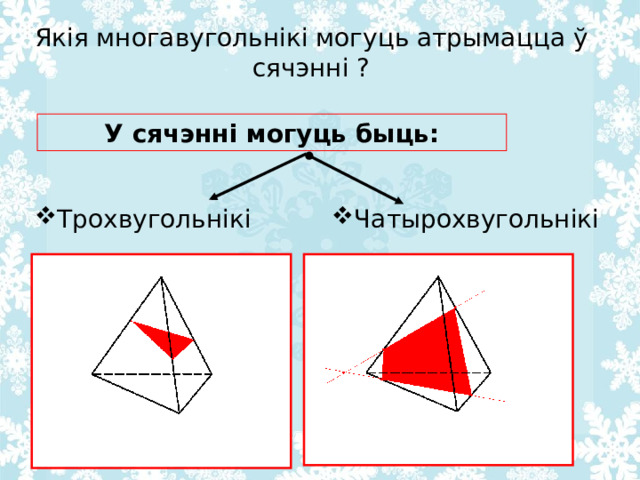
Як ія многавугольнікі могуць атрымацца ў сячэнні ?

У сячэнні могуць быць:

• Чатырохвугольнікі

• Трохвугольнікі

Для пабудавання сячэння трэба пабудаваць пункты перасячэння сякучай плоскасці з кантамі і злучыць іх адрэзкамі.

1. Злучыць можна толькі два пункты, якія ляжаць

у плоскасці адной грані.

2. Сякучая плоскасць перасякае паралельные грані па паралельным адрэзкам.

3. Калі ў плоскасці грані адзначаны толькі адзін пункт,які належыць плоскасці сячэння, то трэба пабудаваць дадатковы пункт. Для гэтага неабходна знайці пункты перасячэння ўжо пабудаваных прамых з другімі прамымі, якія ляжаць у тых жа гранях.

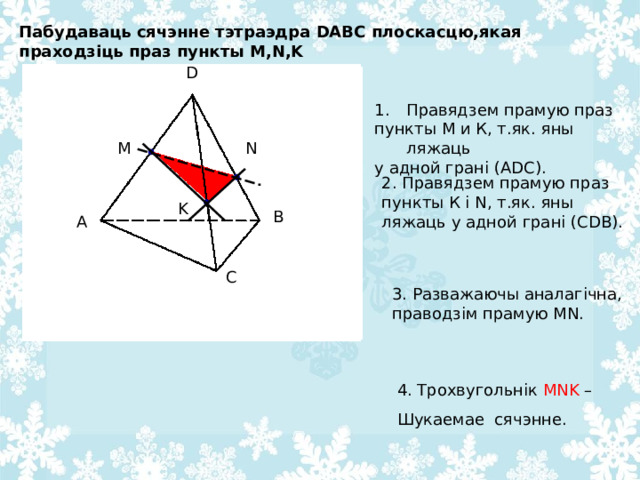
Пабудаваць сячэнне тэтраэдра DABC плоскасцю,якая праходзіць праз пункты M , N , K

D

D

• Правядзем прамую праз

пункты М и К, т.як. яны ляжаць

у адной грані (А DC ).

N

M

2. Правядзем прамую праз пункты К і N , т.як. яны ляжаць у адной грані (С DB ).

K

B

A

B

A

C

C

3. Разважаючы аналагічна, праводзім прамую MN .

4. Трохвугольнік MNK –

Шукаемае сячэнне.

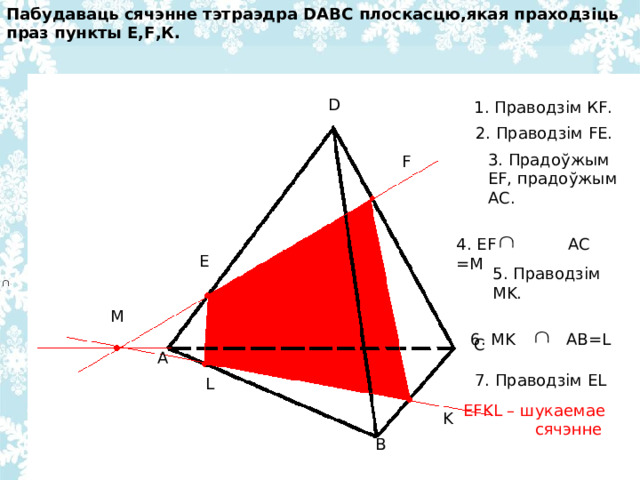
Пабудаваць сячэнне тэтраэдра DABC плоскасцю,якая праходзіць праз пункты Е, F ,К.

D

1. Праводзім К F .

2. Праводзім FE .

3. Прадоўжым EF , прадоўжым AC .

F

4. EF AC = М

E

5. Праводзім MK .

M

6. MK AB=L

C

A

7. Праводзім EL

L

EFKL – шукаемае

сячэнне

K

B

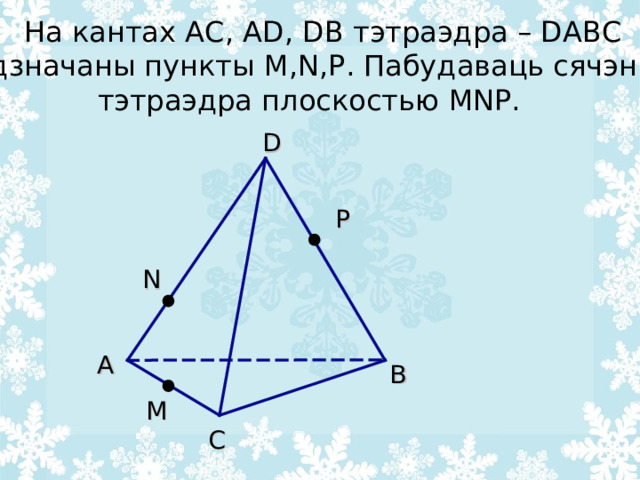
На кантах AC , AD, DB тэтраэдра – DABC

адзначаны пункты M,N,P . Пабудаваць сячэнне

тэтраэдра плоскостью MNP.

D

P

N

А

B

M

C

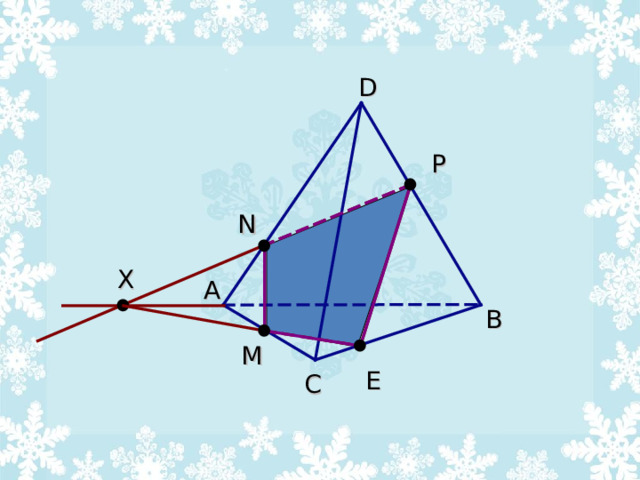
D

P

N

Х

А

B

M

E

C

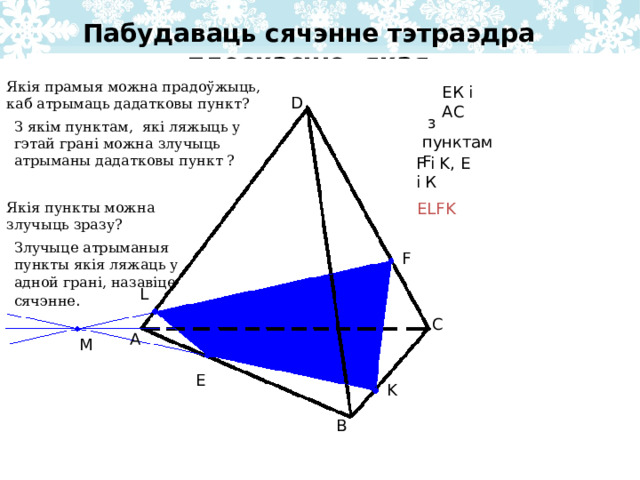
З якім пунктам, які ляжыць у гэтай грані можна злучыць атрыманы дадатковы пункт ?

Е LFK

Пабудаваць сячэнне тэтраэдра плоскасцю, якая

праходзіць праз пункты E , F , K .

Якія прамыя можна прадоўжыць, каб атрымаць дадатковы пункт?

D

з пунктам F

F і K , Е і К

Якія пункты можна злучыць зразу?

Злучыце атрыманыя пункты якія ляжаць у адной грані, назавіце сячэнне .

F

L

C

A

M

E

K

B

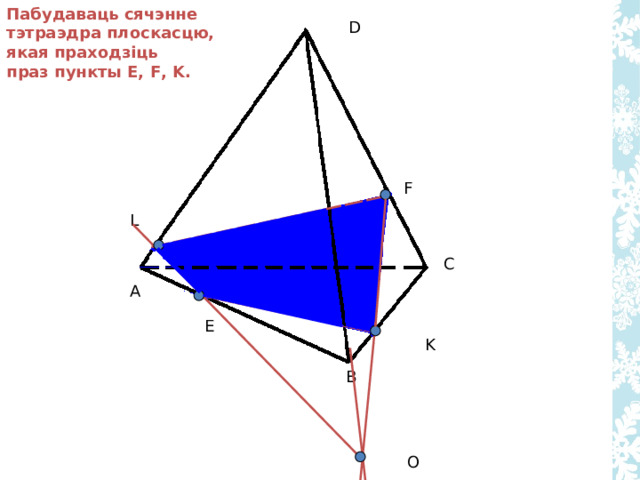
Пабудаваць сячэнне тэтраэдра плоскасцю, якая праходзіць

праз пункты E , F , K .

D

F

L

C

A

E

K

B

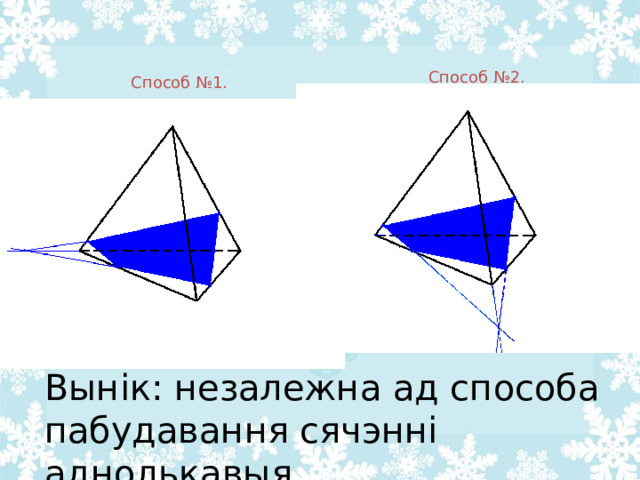
Способ №2.

Способ №1.

Вынік: незалежна ад способа пабудавання сячэнні аднолькавыя.

Вынік УРОКА : Дамашняе заданне:

• Стар .24-29
• П.12, 14
• Выканаць заданні па пабудаванню сячэння тэтраэдра ( карточкі).
• Творчае заданне: зрабіць бумажную модэль тэтраэдра.