Презентация. Трапеция. 8 класс.

ТРАПЕЦИЯ

8 класс

МБОУ «Большаковская СОШ» Яковлева Ирина Владимировна

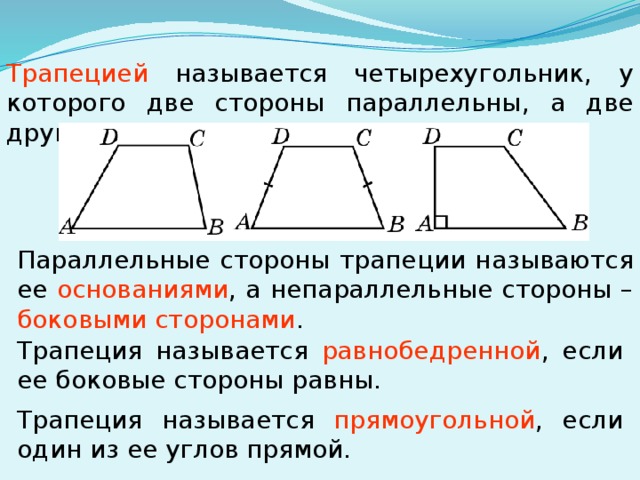
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Параллельные стороны трапеции называются ее основаниями , а непараллельные стороны – боковыми сторонами .

В режиме слайдов ответы появляются после кликанья мышкой

Трапеция называется равнобедренной , если ее боковые стороны равны.

Трапеция называется прямоугольной , если один из ее углов прямой.

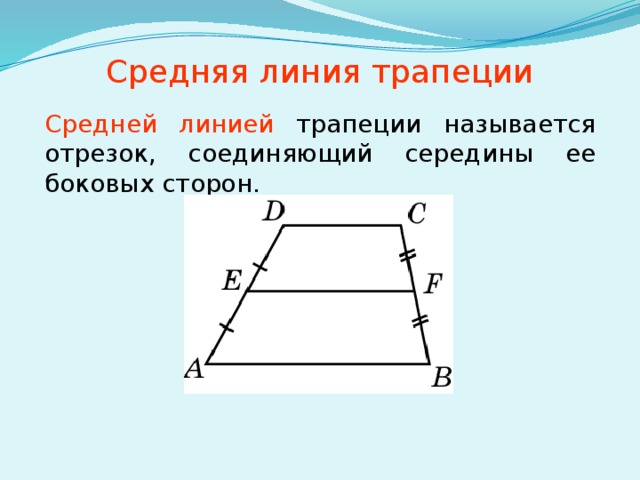
Средняя линия трапеции

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

В режиме слайдов ответы появляются после кликанья мышкой

Теорема о средней линии трапеции

Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство. Пусть EF – средняя линия трапеции ABCD ( AB || CD ). Проведем прямую DF и ее точку пересечения с прямой AB обозначим G .

Треугольники DFC и GFB равны по второму признаку равенства треугольников ( CF = BF по условию, угол 1 равен углу 2, как вертикальные, угол 3 равен углу 4, как накрест лежащие углы). Из равенства этих треугольников следует, что DF = GF и, значит, EF - средняя линия треугольника AGD . Из теоремы о средней линии треугольника следует, что EF параллельна AB и EF = AG . Так как AB || CD , то EF будет параллельна обоим основаниям и кроме того, EF = AG /2 = ( AB + BG )/2 = ( AB + CD )/2.

В режиме слайдов ответы появляются после кликанья мышкой

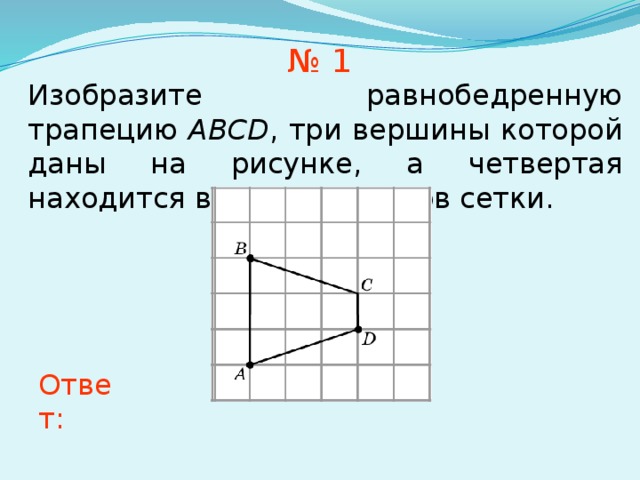
№ 1

Изобразите равнобедренную трапецию ABCD , три вершины которой даны на рисунке, а четвертая находится в одном из узлов сетки.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

5

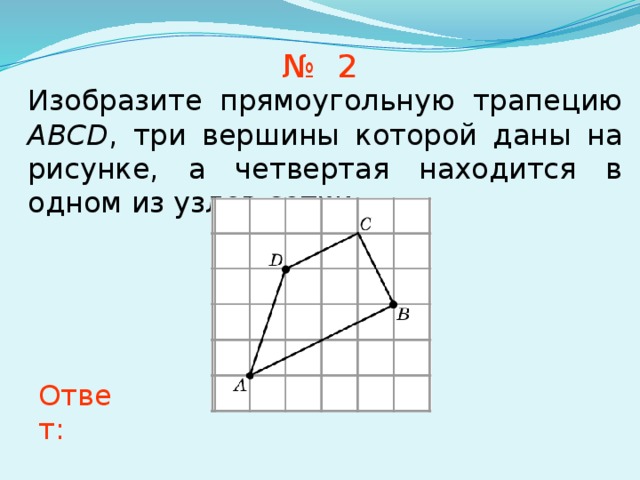
№ 2

Изобразите прямоугольную трапецию ABCD , три вершины которой даны на рисунке, а четвертая находится в одном из узлов сетки.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

6

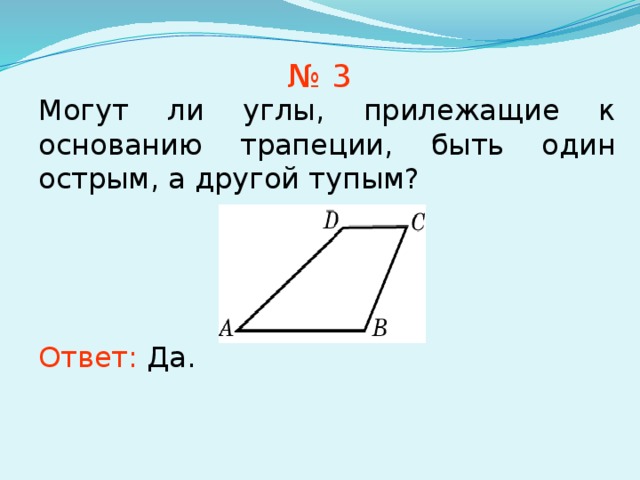
№ 3

Могут ли углы, прилежащие к основанию трапеции, быть один острым, а другой тупым?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: Да.

7

№ 4

Может ли у трапеции быть: а) три прямых угла; б) три острых угла?

Ответ: а) Нет;

б) нет.

В режиме слайдов ответы появляются после кликанья мышкой

7

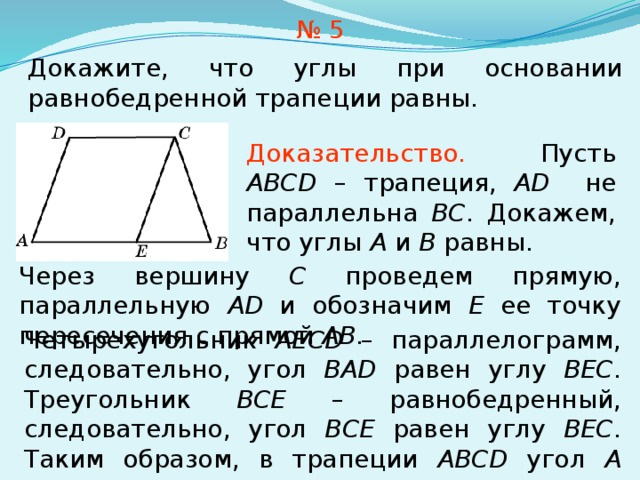
№ 5

Докажите, что углы при основании равнобедренной трапеции равны.

Доказательство. Пусть ABCD – трапеция, AD не параллельна BC . Докажем, что углы A и B равны.

Через вершину C проведем прямую, параллельную AD и обозначим E ее точку пересечения с прямой AB .

В режиме слайдов ответы появляются после кликанья мышкой

Четырехугольник AECD – параллелограмм, следовательно, угол BAD равен углу BEC . Треугольник BCE – равнобедренный, следовательно, угол BCE равен углу BEC . Таким образом, в трапеции ABCD угол A равен углу B .

7

№ 6

Верно ли, что если два угла трапеции равны, то она равнобедренная?

Ответ. Нет, она может быть прямоугольной.

В режиме слайдов ответы появляются после кликанья мышкой

7

№ 7

Верно ли, что если два угла при основании трапеции равны, то она равнобедренная?

Ответ. Да.

В режиме слайдов ответы появляются после кликанья мышкой

7

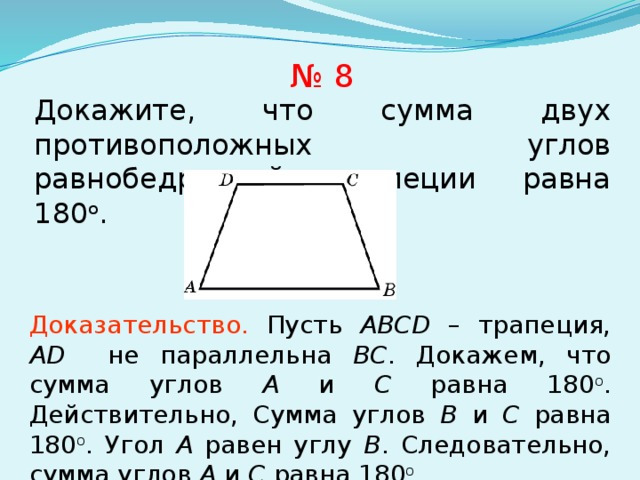
№ 8

Докажите, что сумма двух противоположных углов равнобедренной трапеции равна 180 о .

В режиме слайдов ответы появляются после кликанья мышкой

Доказательство. Пусть ABCD – трапеция, AD не параллельна BC . Докажем, что сумма углов A и С равна 180 о . Действительно, Сумма углов B и C равна 180 о . Угол A равен углу B . Следовательно, сумма углов A и С равна 180 о .

7

№ 9

Чему равны углы равнобедренной трапеции, если известно, что разность противолежащих углов равна 40 о ?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 7 0 о , 110 о , 70 о , 110 о .

7

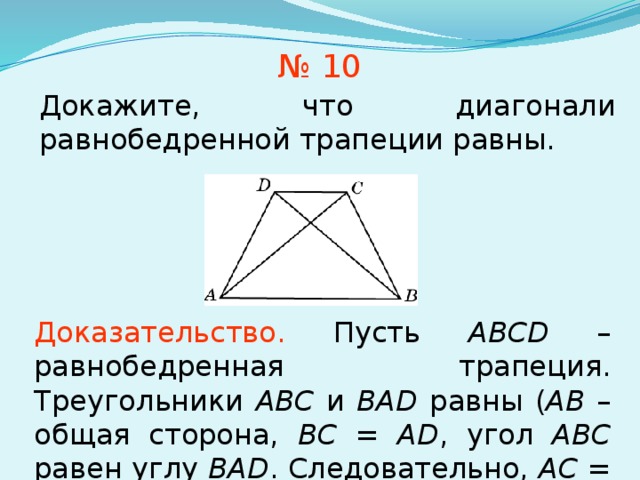
№ 10

Докажите, что диагонали равнобедренной трапеции равны.

В режиме слайдов ответы появляются после кликанья мышкой

Доказательство. Пусть ABCD – равнобедренная трапеция. Треугольники ABC и BAD равны ( AB – общая сторона, BC = AD , угол ABC равен углу BAD . Следовательно, AC = BD .

7

Верно ли, что если диагонали трапеции равны, то она равнобедренная?

№ 11

Ответ. Да.

В режиме слайдов ответы появляются после кликанья мышкой

7

№ 12

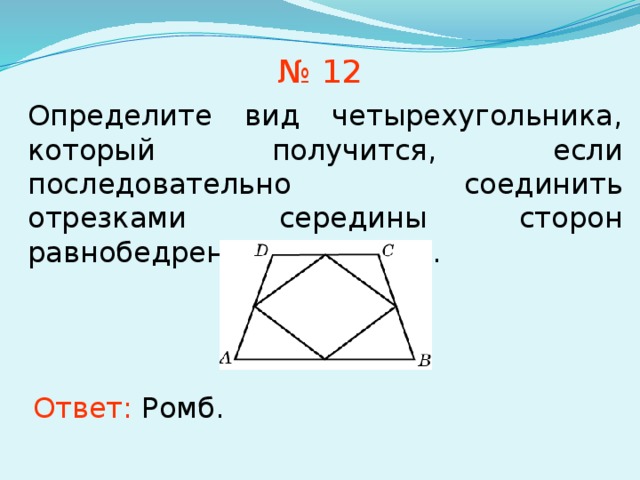
Определите вид четырехугольника, который получится, если последовательно соединить отрезками середины сторон равнобедренной трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: Ромб.

16

№ 13

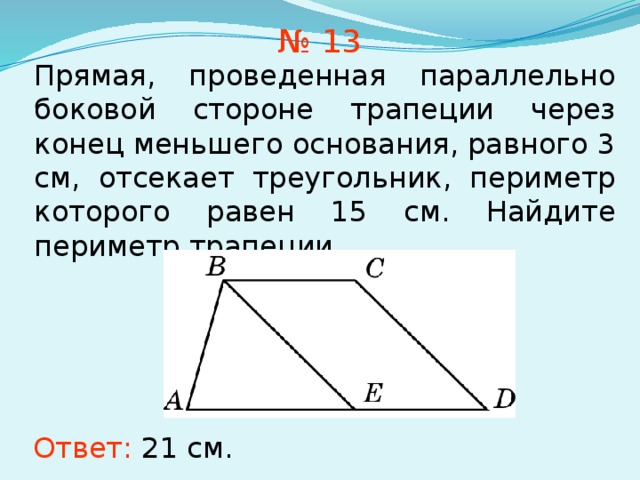
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 3 см, отсекает треугольник, периметр которого равен 15 см. Найдите периметр трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 21 см.

16

№ 14

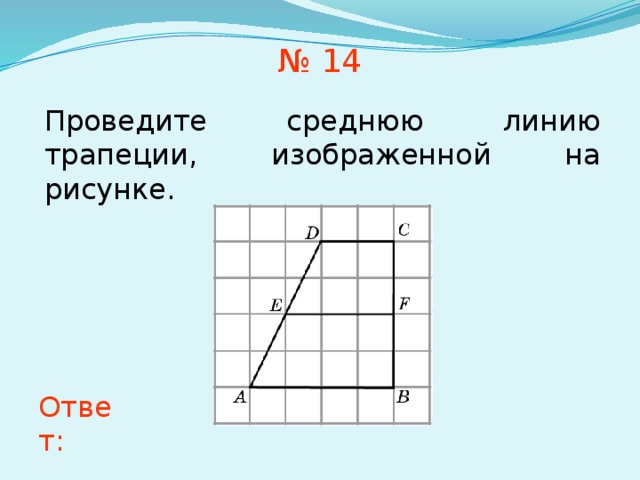
Проведите среднюю линию трапеции, изображенной на рисунке.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

18

№ 15

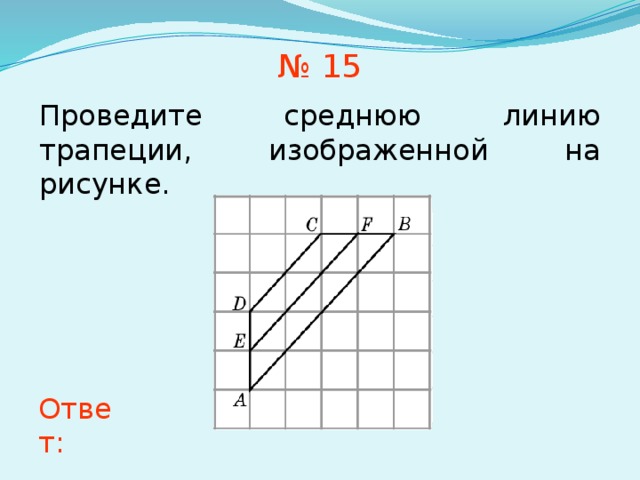
Проведите среднюю линию трапеции, изображенной на рисунке.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

19

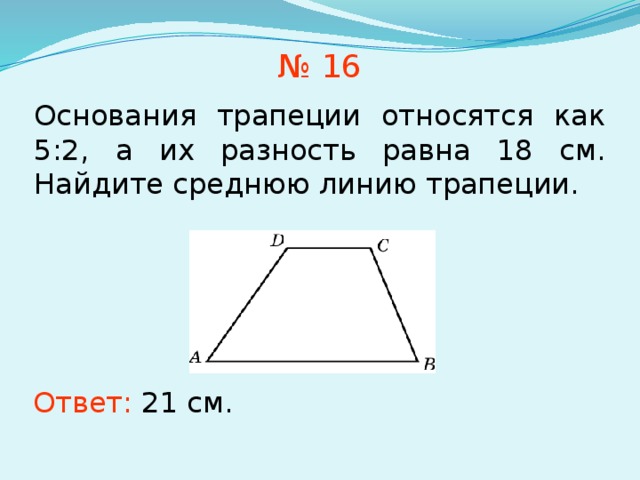
№ 16

Основания трапеции относятся как 5:2, а их разность равна 18 см. Найдите среднюю линию трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 21 см.

19

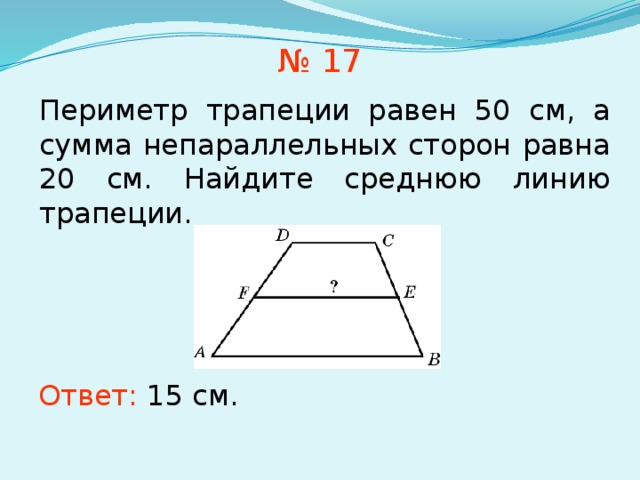
№ 17

Периметр трапеции равен 50 см, а сумма непараллельных сторон равна 20 см. Найдите среднюю линию трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 15 см.

19

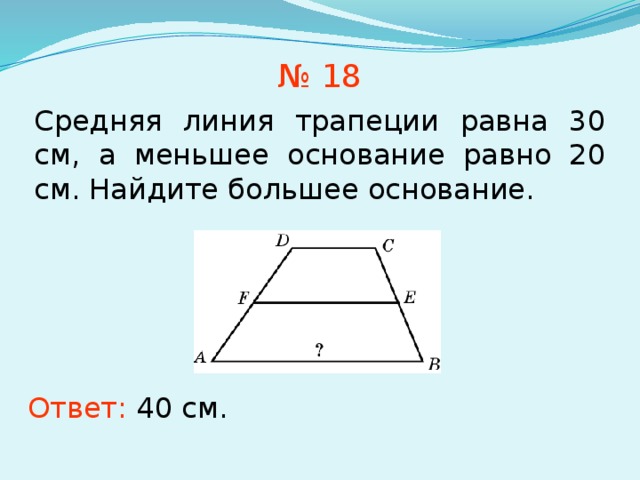
№ 18

Средняя линия трапеции равна 30 см, а меньшее основание равно 20 см. Найдите большее основание.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 40 см.

19

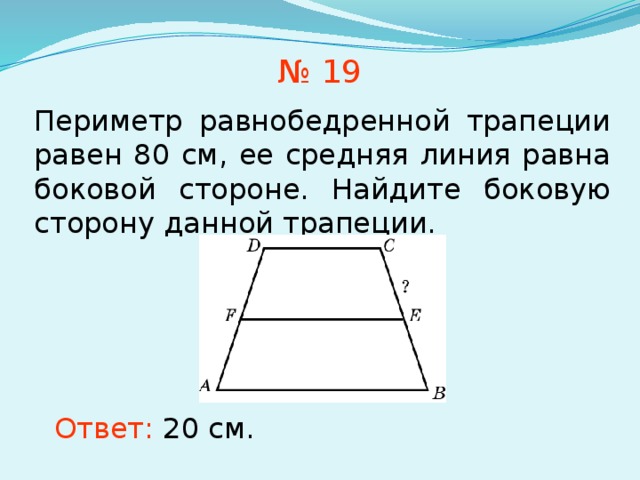
№ 19

Периметр равнобедренной трапеции равен 80 см, ее средняя линия равна боковой стороне. Найдите боковую сторону данной трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 20 см.

19

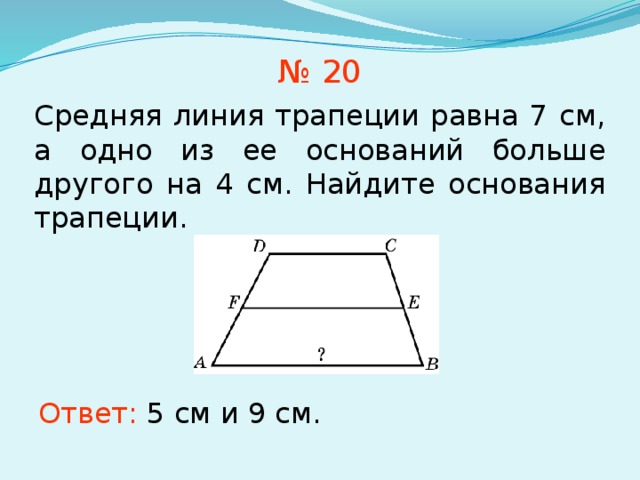
№ 20

Средняя линия трапеции равна 7 см, а одно из ее оснований больше другого на 4 см. Найдите основания трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 5 см и 9 см.

19

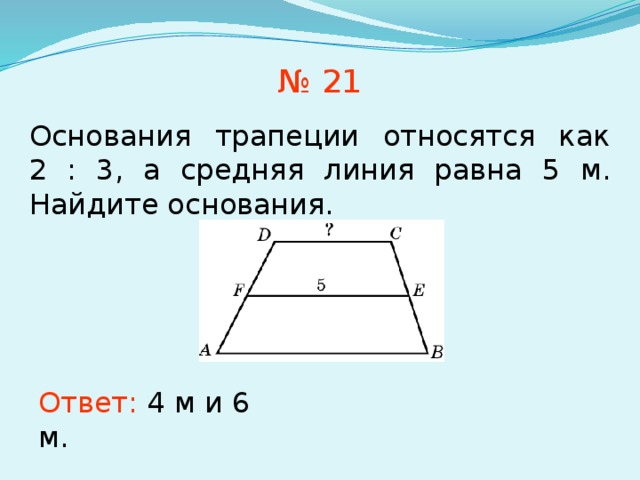
№ 21

Основания трапеции относятся как 2 : 3, а средняя линия равна 5 м. Найдите основания.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 4 м и 6 м.

19

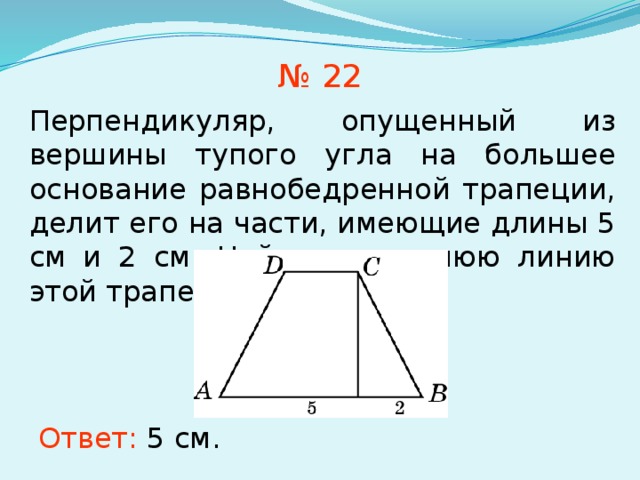
№ 22

Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 5 см и 2 см. Найдите среднюю линию этой трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 5 см.

19

№ 23

В равнобедренной трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60 о . Найдите меньшее основание.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 1,7 м.

19

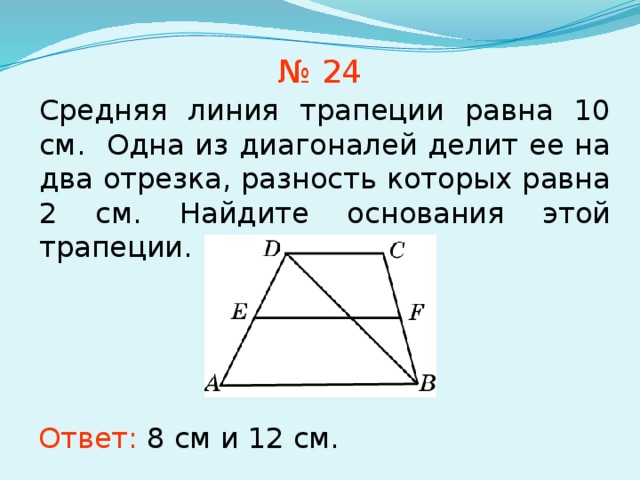
№ 24

Cредняя линия трапеции равна 10 см. Одна из диагоналей делит ее на два отрезка, разность которых равна 2 см. Найдите основания этой трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 8 см и 12 см.

19

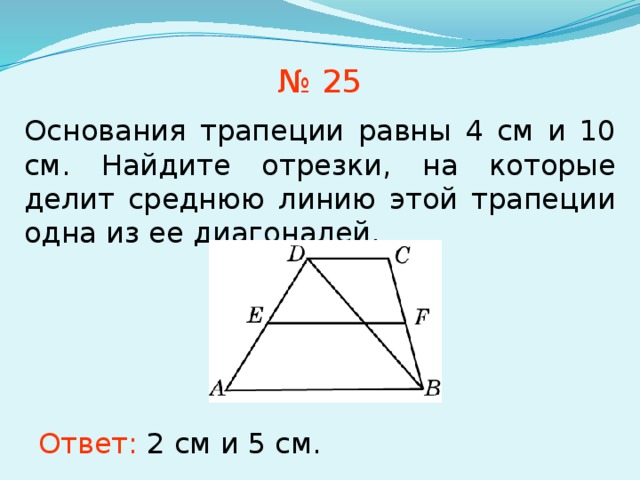
№ 25

Основания трапеции равны 4 см и 10 см. Найдите отрезки, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 2 см и 5 см.

19

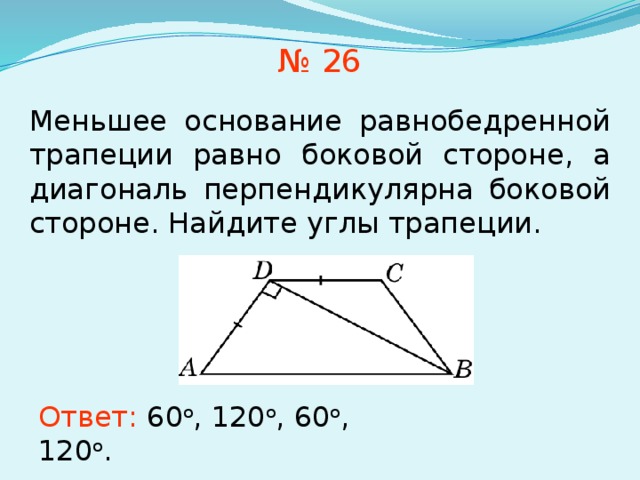
№ 26

Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 60 о , 120 о , 60 о , 120 о .

19

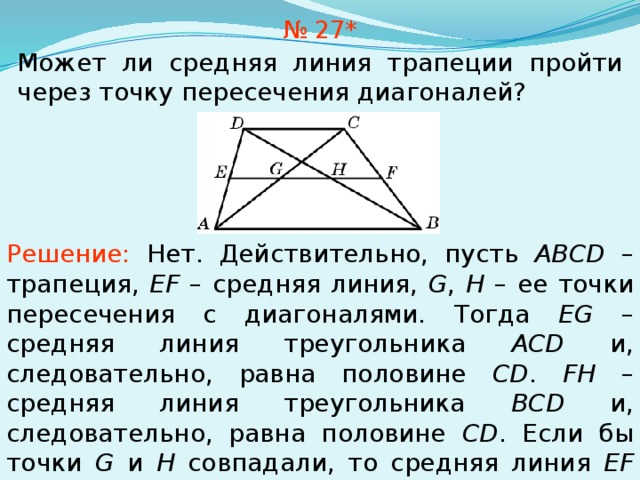
№ 27*

Может ли средняя линия трапеции пройти через точку пересечения диагоналей?

Решение: Нет. Действительно, пусть ABCD – трапеция, EF – средняя линия, G , H – ее точки пересечения с диагоналями. Тогда EG – средняя линия треугольника ACD и, следовательно, равна половине CD . FH – средняя линия треугольника BCD и, следовательно, равна половине CD . Если бы точки G и H совпадали, то средняя линия EF была бы равна CD . В этом случае трапеция была бы параллелограммом.

В режиме слайдов ответы появляются после кликанья мышкой

31

Использованы ресурсы: