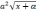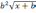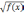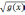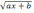Элективный курс по математике
для 10 класса
"Практикум по решению задач повышенной сложности"
Автор: Задворнова Т.Н.
2017 – 2018 уч. год
Пояснительная записка
Основная задача обучения математики – обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждого человека, достаточных для изучения смежных дисциплин и продолжения образования.
Наряду с решением основной задачи данный курс предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, требующие математической подготовки.
Программа включает в себя основные разделы курсов основной и средней школ по алгебре и началам анализа и ряд дополнительных вопросов, непосредственно примыкающих к этому курсу и углубляющих его по основным идейным линиям.
Данная программа предназначена для занятий в 10 классе.
Программа поможет учащимся старших классов углубить свои математические знания, поможет с разных точек зрения взглянуть на уже известные темы, значительно расширить круг математических вопросов, которые не изучаются в школьном курсе.
Каждое занятие направлено на то, чтобы развить интерес школьников к предмету, а главное, порешать интересные задачи повышенного уровня. Расширяя математический кругозор, программа значительно совершенствует технику решения сложных, конкурсных и олимпиадных заданий.
Этот курс предлагает учащимся знакомство с математикой как с общекультурной ценностью, выработкой понимания ими того, что математика является инструментом познания окружающего мира и самого себя.
Элективный курс «Практикум решения задач повышенной сложности» рассчитан на 68 часов и предусматривает повторное рассмотрение теоретического материала по математике, а кроме этого, нацелен на более глубокое рассмотрение отдельных тем, поэтому имеет большое общеобразовательное значение.
Основные цели курса:
оказание индивидуальной, систематической помощи выпускнику при систематизации, обобщении теории курса алгебры, геометрию;
создание условий для развития творческого потенциала при решении задач повышенной сложности.
Основные задачи курса:
Обучающие:
Развивающие:
развитие умения уметь самостоятельно работать с таблицами и справочной литературой;
развитие умения составлять алгоритмы решения текстовых и геометрических задач;
развитие умения решать тригонометрические, показательные и логарифмические уравнения и неравенства;
развитие умения применять различные методы исследования элементарных функций и построения их графиков;
Воспитательные:
рассмотреть практическую значимость использования математических знаний в повседневной жизни, а также как прикладного инструмента в будущей профессиональной деятельности;
создать положительную мотивацию обучения;
воспитание аккуратности, последовательности в действиях, умение чётко выражать свои мысли.
Курсу отводится по 2 часа в неделю. всего 68 учебных часов.
Требования к учащимся: учащийся должен знать/уметь:
уметь решать задания повышенной сложности;
уметь самостоятельно работать с таблицами и справочной литературой;
уметь составлять алгоритмы решения типичных задач;
уметь решать тригонометрические, показательные и логарифмические уравнения и неравенства;
знать методы исследования элементарных функций
знать, как используются математические формулы, примеры их применения для решения математических и практических задач;
знать, как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
уметь использовать математические знания в повседневной жизни, а также как прикладного инструмента в будущей профессиональной деятельности.
Содержание курса
Алгебраические уравнения и неравенства
Неравенства – одна из важнейших тем в школьном курсе математики. В данном разделе вспомним, прежде всего, метод интервалов для рациональных функций.
Рассмотрим иррациональные уравнения и уравнения, содержащие модуль или квадратный корень. Приведём условия равносильности. Всё это даёт возможность решать уравнения быстрее, что важно для выполнения, например, заданий ЕГЭ.
Понятие равносильности уравнений и неравенств.
Система уравнений и неравенств. Совокупность уравнений и неравенств.
Квадратные уравнения и сводящиеся к ним.
Рациональные неравенства. Метод интервалов.
Уравнения вида l f( x) l = g (x).
Уравнения вида 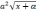
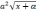 +
+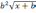
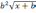 = const.
= const.
Уравнения вида 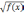
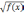 = g(x). Уравнения вида
= g(x). Уравнения вида 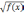
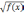 =
=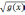
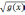 .
.
Возвратные уравнения.
Задачи с параметрами.
Графики и множества на плоскости.
Во многих задачах бывает необходимо каким-то способом математически описать зависимость одной из изучаемых величин от другой величины.
Зависимость разных величин друг от друга описывают по-разному. Это можно делать с помощью формул, уравнений, неравенств или систем. Но часто
полезно наглядно показать рассматриваемую зависимость так, чтобы были
видны её свойства при тех или иных значениях рассматриваемых величин.
Тогда и возникает необходимость решать задачи на построение графиков
функций и уравнений. Иногда это сделать нетрудно, а иногда возникают
тонкости, с которыми связано множество задач повышенной сложности.
Некоторые классы таких задач предлагаются на ЕГЭ, математических
олимпиадах и вступительных экзаменах в ведущие высшие учебные заведения.
Построение графиков функций, заданных на промежутках.
Построение графиков целой и дробной части числа.
Преобразования графиков функций и уравнений.
Построение графиков дробно-линейных функций.
Построение графиков с модулями методом интервалов.
Метод областей на координатной плоскости.
Графики функций и уравнений в задачах с параметрами
Планиметрия.
В данном разделе рассматривается на применении теорем синусов и косинусов различные формулы площади, повторяются свойства трапеции, основное внимание уделяется приёмам решения задач. Цель раздела продемонстрировать различные методы и подходы к решению задач. доказать новые утверждения и получить полезные формулы.
Тригонометрические функции и уравнения.
Тема, которая дается учащимся особенно сложно. Задача раздела обобщить способы решения задач, расширить поле применения данной темы в задачах повышенной сложности.
Чётность и периодичность
Тригонометрические преобразования.
Тригонометрические уравнения.
Однородные уравнения.
Использование формулы дополнительного угла.
Рациональные тригонометрические уравнения.
Тригонометрические уравнения с корнем.
Тригонометрические уравнения с модулем.
Уравнения с параметром.
Тематическое планирование курса в 10 классе
| | Название темы | Кол-вочасов |
| 1 | Алгебраические уравнения и неравенства. | 22 |
| 2 | Графики и множества на плоскости. | 12 |
| 3 | Планиметрия. | 10 |
| 4 | Тригонометрические функции и уравнения | 34 |
| Всего | 68 |
Календарно – тематическое планирование
| № | Содержание материала | Количество часов |
| Алгебраические уравнения и неравенства ( 22 часа) |
| 1 | Понятие равносильности уравнений и неравенств. | 1 |
| 2 | Системы уравнений и неравенств. | 1 |
| 3 | Квадратные уравнения и сводящиеся к ним. | 1 |
| 4 | Рациональные неравенства. Метод интервалов. | 1 |
| 5 | Уравнения вида ׀f(x)׀=g(x) | 2 |
| 6 | Уравнения вида ׀f(x)׀= ׀g(x)׀ | 2 |
| 7 | Уравнения вида 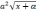 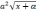 + +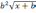 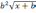 = const = const | 2 |
| 8 | Уравнения вида 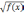 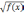 = g(x) = g(x) | 2 |
| 9 | Уравнения вида 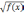 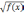 = =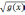 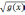 | 2 |
| 10 | Уравнение вида 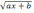 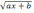 = cx+d = cx+d | 2 |
| 11 | Возвратные уравнения. | 2 |
| 12 | Задачи с параметрами. | 4 |
| Графики и множества на плоскости. (12 часов) |
| 1 | Построение графиков функций, заданных на промежутках. | 2 |
| 2 | Построение графиков целой и дробной части числа. | 2 |
| 3 | Преобразования графиков функций и уравнений. | 2 |
| 4 | Построение графиков дробно-линейных функций. | 2 |
| 5 | Построение графиков с модулями методом интервалов. | 2 |
| 6 | Графики функций и уравнений в задачах с параметрами | 2 |
| Планиметрия. (10 часов) |
| 1 | Теоремы косинусов и синусов. | 2 |
| 2 | Площадь треугольника. Метод площадей. | 4 |
| 3 | Лемма о биссектрисе. | 2 |
| 4 | Свойства трапеции | 2 |
| Тригонометрические функции и уравнения ( 34 часа) |
| 1 | Чётность и периодичность | 2 |
| 2 | Тригонометрические преобразования | 2 |
| 3 | Тригонометрические уравнения | 6 |
| 4 | Однородные уравнения. | 4 |
| 5 | Использование формулы дополнительного угла | 2 |
| 6 | Рациональные тригонометрические уравнения | 2 |
| 7 | Тригонометрические уравнения с корнем | 4 |
| 8 | Тригонометрические уравнения с модулем | 4 |
| 9 | Нестандартные уравнения | 4 |
| 10 | Уравнения с параметром | 4 |
Изучение каждой темы заканчивается самостоятельной работой, которая позволяет проверить знания и умения.
Организация работы на занятиях должна несколько отличаться от работы на уроке: ученику необходимо давать время на размышление, учить рассуждать, и, тем самым, самостоятельно добиваться результата.
Предлагаемый элективный курс соответствует:
Учебно методические обеспечение курса.
Курс обеспечен раздаточным материалом, подготовленным на основе прилагаемого ниже списка литературы.
Литература:
УМК « Математика.ЕГЭ-2017», « Математика. Математические тесты, геометрия,», 10-11 классы, под редакцией Ф.Ф. Лысенко, « Легион-М, Ростов-на-Дону,2017.
М. Шамшин «Тематические тесты для подготовки к ЕГЭ по математике», ФЕНИКС 2017г.
«Изучение сложных тем курса алгебры в средней школе» МОСКВА
П.Ф.Севрюков, А.Н.Смоляков «Тригонометрические уравнения и неравенства и методика их решения» СТАВРОПОЛЬ 2004г.
С.Н. Олехник, М.К. Потапов, П.И. Пасиченко «Уравнения и неравенства. Нестандартные методы решения», ДРОФА 2003 г.
Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами.- М.: Илекса, Харьков: Гимназия, 2015 г.,-328 с.
А.Л, Ершова « Самостоятельные, и контрольные
работы по алгебре и началам анализа в 10-11 классах», ИЛЕКСА Москва 2008
С.А Шестаков и др. Сборник задач для подготовки к проведению
итоговой аттестации за курс средней школы»,