152
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В ФОРМЕ ГРАФА
ПОНЯТЬ
Вы, вероятно, имеете представление о компьютерных сетях. Возможно, компьютеры в школьном кабинете информатики объединены в локальную сеть или вы работали в Internet, или пользовались услугами электронной почты. Понятно, что сеть образуется только тогда, когда компьютеры соединены между собой каналами передачи данных каким-либо образом.
Размещение абонементов сети (подключенных к ней ЭВМ или других систем автоматической обработки данных) и способ их соединения друг с другом называется конфигурацией сети. Продемонстрировать различные типы конфигураций вычислительных сетей можно, например, с помощью таких информационных моделей, как графы.
Граф - совокупность точек, соединенных между собой линиями. Точки называют вершинами графа. Они могут изображаться точками, кружочками, прямоугольниками и пр. Линии, соединяющие вершины, называются дугами (если задано направление от одной вершины к другой) или ребрами (если направленность двусторонняя, то есть направления равноправны).
Две вершины, соединенные ребром (дугой) называются смежными.
Вершины и ребра графа могут характеризоваться некоторыми числовыми величинами. Например, может быть известна длина ребра или “стоимость прохождения” по нему. Такие характеристики называют весом, а граф называется взвешенным.
Граф однозначно задан, если заданы множество его вершин, множество ребер (дуг) и указано, какие вершины какими ребрами соединены и, возможно, указаны веса вершин и ребер (дуг). Определение всех этих элементов и составляет суть формализации в этом случае.
ПРИМЕР
На рисункt 2.5.1 представлены различные типы конфигураций локальных вычислительных сетей (ЛВС), являющиеся информационными моделями структур ЛВС, представленными в виде графов.
шинная, когда к незамкнутому каналу с некоторыми интервалами подключаются отдельные абоненты (К), информация от абонента-источника распространяется по каналу в обе стороны;
кольцевая, когда каждый абонент непосредственно связан с двумя соседними абонентами, а информация передается по замкнутому кольцу, чаще всего в одну сторону;
звездообразная, в центре которой находится центральный коммутатор (ЦК), который последовательно “опрашивает” абонентов и предоставляет им право на обмен данными;
древовидная конфигурация образуется подсоединением нескольких простых каналов связи к одному магистральному;
полносвязные конфигурации обеспечивают выбор наиболее быстрого маршрута связи между абонентами и удобны там, где управление оказывается достаточно сложным.
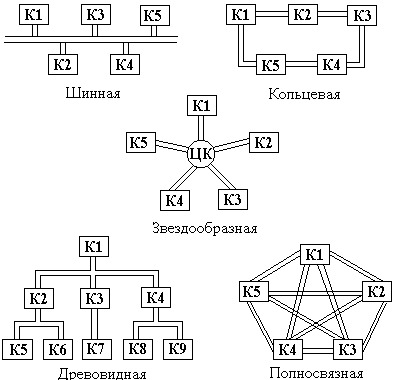
Рис. 2.5.1. Различные типы конфигураций локальных компьютерных сетей
Наиболее наглядно граф задается рисунком. Однако не все детали рисунка одинаково важны. В частности, несущественны геометические свойства ребер (длина, кривизна и т.д.), форма вершин (точка, кружок, квадрат, овал и пр.) и взаимное расположение вершин на плоскости. Так, на рисунке 2.5.2 представлены два изображения одного и того же графа.
Вес вершины и ребра часто задается в виде сопровождающей надписи на вершине или линии, но, введя условные обозначения, их можно задать формой или цветом вершины, толщиной, типом или цветом линии и т.п.
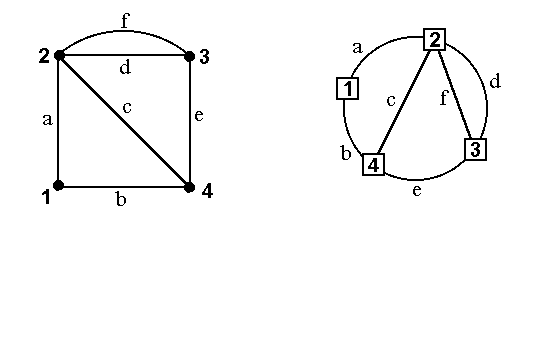
Рис. 2.5.2. Различное изображение одного и того же графа
Информационную модель в форме графа можно использовать для наглядного представления взаимосвязей, существующих меду элементами объекта моделирования. Таким образом, граф наиболее удобная форма для моделирования структуры объекта, хотя в такой форме можно моделировать и нешний вид и поведение объекта.
ПРИМЕР
На рисунке 2.5.3 представлены модели молекул бутана и изобутана, каждая из которых имеет формулу С4Н10, то есть состоит из четырех атомов углерода и десяти атомов водорода.
Имея одну и ту же формулу, бутан и изобутан имеют различные химические свойства, так как способы соединения атомов (структура молекул) различны. Расположение атомов в молекуле при различных способах их соединения хорошо представимо графом.
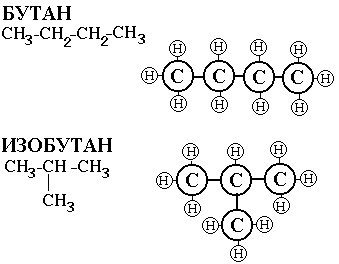
Рис. 2.5.3. Модели молекул бутана и изобутана
Заметим, что в химии для обозначения таких веществ часто используются и структурные формулы. Порядок соединения атомов изображается в структурной формуле черточками (связь между водородом и остальными атомами обычно не указывается). Можно ли считать структурную формулу одной из разновидностей графа, подумайте сами.
В форме графа удобно отображать взаимосвязи понятий, относящихся к одной области деятельности или познания. Например, логическая схема понятий раздела “Моделирование и формализация” (стр. ...) - не что иное, как граф. А если снабдить такую схему сопроводительными надписями, то можно сделать удобную для себя памятку.
ПРИМЕР
Рассмотрите граф понятий темы “Четырехугольники” из курса геометрии. Не правда ли, хорошая “шпаргалка”?
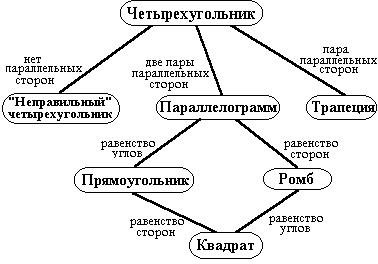
Рис. 2.5.4. Граф понятий темы “Четырехугольники”
В практической деятельности модели в форме графов часто используются для представления видов и порядка выполнения работ. Возможно, вам знакомы такие названия, как “сетевой график работ”, “сетевой график строительства”. Часто наряду со словесным или табличным описанием сетевые графики сопровождаются и изображением в виде графа, вершинами которого являются конкретные виды работ, а дугами задается возможный порядок их выполнения.
ПРИМЕР
Сетевые графики строительства хорошо демонстрируют, какие работы могут выполняться одновременно, а какие требуют обязательного завершения предыдущих этапов. Анализируя такие графы можно рассчитать время, необходимое для завершения всей работы, спланировать, сколько, когда и на какие работы направить специалистов и технику, определить наиболее “узкие” участки и уделить им особое внимание.
Для машинной обработки более удобным является символическое представление графов в виде списка ребер с указанием, какие вершины это ребро соединяет, а также табличное представление, где строки и столбцы - названия вершин, а значения ячеек указывают на то, соединены данные вершины или нет.
ПРИМЕР
Графы, представленные на рисунке 2.5.5 могут быть описаны, например, следующими способами.
Символическая запись: a(1,2) b(1,4) c(2,4) d(2,3) e(3,4) f(2,3)
Табличная запись:
|
| 1 | 2 | 3 | 4 |
| 1 | 0 | 1 | 0 | 1 |
| 2 | 1 | 0 | 2 | 1 |
| 3 | 0 | 2 | 0 | 1 |
| 4 | 1 | 1 | 1 | 0 |
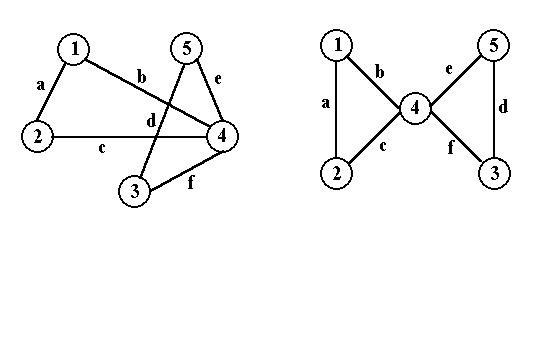
Рис. 2.5.5.
ПРЕДСТАВЛЕНИЕ ДАННЫХ В ФОРМЕ ДЕРЕВА
Особым видом графа является дерево. Данная форма модели применяется тогда, когда элементы моделируемого объекта находятся в состоянии какого-либо подчинения и соподчинения, когда есть отношение иерархичности.
ПРИМЕР
Модель управления предприятием (школой, театральным коллективом и т.д.) очень удобно представлять в виде дерева.
ПРИМЕР
Вам хорошо известно понятие “родословное дерево” и вы можете изобразить в такой форме ваши родственные отношения.
ПРИМЕР
Каталог файлов на диске, так же как и библиотечный каталог - примеры информационных моделей в форме дерева.
Формализация в случае построения дерева (иерархического графа) сводится к выявлению основного (главного, центрального) элемента рассматриваемого объекта (вершина 0-го уровня, которую часто называют “корнем), элементов, которые находятся в непосредственном “подчинении” от основного (вершины 1-го уровня). Затем выявляются вершины, находящиемся в непосредственном “подчинении” от вершин 1-го уровня (вершины 2-го уровня) и т.д. Изображать построенное дерево отношений можно в любом направлении - это уже дело эстетического вкуса разработчика модели.
В научной и учебной деятельности с помощью деревьев часто представляют классификацию изучаемых объектов.
Классифицирование - распределение объектов по классам в зависимости от их общих признаков, фиксирующее закономерные связи между классами объектов в единой системе данной отрасли знания.
Классификация (от лат. classis разряд + facere делать) - система соподчиненных понятий (классов объектов, явлений) в какой-либо отрасли знания, составленная на основе учета общих признаков объектов и закономерных связей между ними.
Классификация позволяет ориентироваться в многообразии объектов и является источником знания о них. Очень важен выбор основания классификации - то есть признака, на основании которого объекты разбиваются на классы. Выбор разных оснований приводит к разным классификациям.
ПРИМЕР 9
На рисунке 2.5.6 вы видите классификацию, предложенную Григорием Великим, которая призвана была показать, что человек имеет что-то общее со всеми видами существующих в мире вещей и поэтому его справедливо называют “вселенной в миниатюре”. Обратите внимание, что объекты здесь разбиваются всегда на два класса. Такая классификация носит название дихотомической.
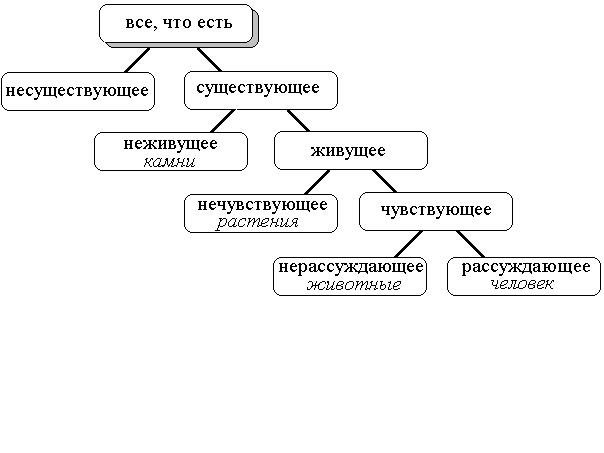
Рис. 2.5.6. Классификация всего существующего Григория Великого
ПРИМЕР 10
Представленная на рисунке 2.5.7 классификация принтеров построена с использованием различных оснований деления.
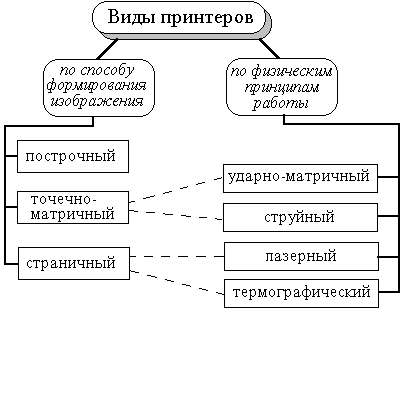
Рис. 2.5.7. Классификация принтеров
ПРИМЕР 11
Важным видом исторических классификаций является построение родословных или генеалогических деревьев. Они бывают самого разного вида: с указанием только прямых потомков (см. рис. 2.5.8), с включением жен (мужей) и их родственников и др.
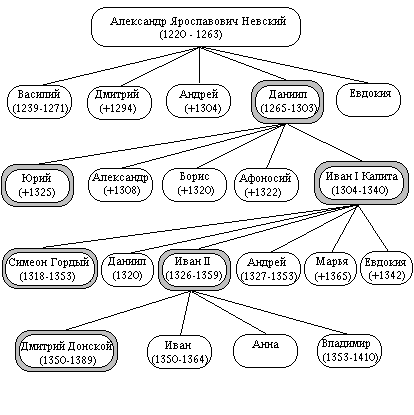
Рис. 2.5.8 Родословное дерево великих и удельных князей
Владимирских и Московских (XIII - XIV вв) (фрагмент)
В скобках приведены известные даты жизни; плюс указывает на год смерти; двойным контуром обведены имена князей, занимавших московский престол.
ВАЖНОЕ ЗАМЕЧАНИЕ
Рассмотренные выше реляционная (табличная), сетевая (графовая) и иерархическая (древовидная) модели являются основными для представления данных в базах данных, а программные комплексы, которые поволяют создавать, обновлять, сохранять базы данных и обслуживать запросы пользователей к ним соответственно называются реляционной, сетевой, иерархичной системой управления базами данных (СУБД). При описании сложных объектов, как правило, используются различные модели данных, вернее комбинация этих моделей.
ЗНАТЬ
Граф - совокупность точек, соединенных между собой линиями.
Точки называют вершинами графа.
Линии, соединяющие вершины, называются дугами, если задано направление от одной вершины к другой, или ребрами, если направленность двусторонняя.
Граф называется взвешенным, если вершины или ребра (дуги) характеризуются некоторой дополнительной информацией - весом вершины или ребра (дуги).
Граф однозначно задан, если заданы множество его вершин, множество ребер (дуг) и указано, какие вершины какими ребрами соединены.
Формализация при построении графа включает в себя следующие этапы:
выявление всех элементов объекта;
элементов (названий, номеров, весов и т.п.);
установлении наличия и вида связи (односторонняя или двухсторонняя) между элементами;
определение характеристик связей - весов ребер и дуг;
выбрать форму изображения вершин и ребер, ввести условные обозначения в случае необходимости;
представление выделенных элементов и связей в графическом виде.
Для компьютерного моделирования более удобным является символическое и/или табличное задание графа.
Символическое задание графа - перечисление всех его ребер с указанием вершин, которые они соединяют либо перечисление всех вершин с указанием исходящих из них ребер.
Дерево - особый вид графа, когда моделируется объект, элементы которого находятся в отношении иерархии (подчинения и соподчинения).
Дерево - связный неориентированный граф без циклов.
Корнем дерева называется вершина, соответствующая основному (центральному, главному, родовому) элементу моделируемого объекта. Листьями дерева называют вершины графа, у которых нет “подчиненных” вершин.
Формализация при построении дерева сводится к выявлению основного элемента рассматриваемого объекта (вершина 0-го уровня - корень дерева), элементов, которые находятся в непосредственном подчинении у основного элемента (вершины 1-го уровня), элементов, находящихся в непосредственном подчинении у вершин 1-го уровня (вершины 2-го уровня) и т.д.
Классификация - система соподчиненных понятий (классов объектов, явлений) в какой-либо отрасли знания, составленная на основе учета общих признаков объектов и закономерных связей между ними. Представляется чаще всего в виде иерархического графа (дерева) или таблицы.
Реляционная (табличная), сетевая (графовая) и иерархическая (древовидная) модели являются основными для представления данных в базах данных.
Программные комплексы, которые поволяют создавать, обновлять, сохранять базы данных и обслуживать запросы пользователей к ним соответственно называются реляционной, сетевой, иерархичной системой управления базами данных (СУБД).
Большинство существующих автоматизированных баз данных являются базами данных реляционного типа.
УМЕТЬ
ЗАДАНИЕ 1
Модели молекул химических веществ даны в форме графа. Записать их химические и структурные формулы.
| Название вещества | Химическая формула | Структурная формула | Модель в форме графа |
| Циклопропан |
|
| 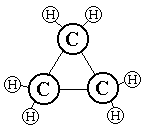 Рис. 2.5.9 (1) |
| Циклогексан |
|
| 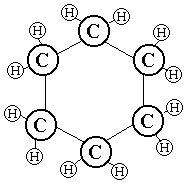 Рис. 2.5.9 (2) |
ЗАДАНИЕ 2
В первом примере параграфа рассматриваются различные структуры локальных сетей. Найдите литературу, посвященную глобальной сети Internet, и попробуйте изобразить структуру этой сети в форме графа. Можете воспользоваться для создания рисунка известным вам графическим редактором.
ЗАДАНИЕ 3
Возьмите топографическую карту вашей местности. Выберите несколько населенных пунктов, находящихся в одном районе. Смоделируйте их расположение в форме графа. Отразите наличие дорог, соединяющие эти населенные пункты и расстояние между ними. Какую еще дополнительную информацию можно представить на графе? Воспользуйтесь для создания рисунка графическим редактором.
ЗАДАНИЕ 4
Постройте граф по словесному описанию.
Для ввода в память ЭВМ текстовой, числовой, графической, звуковой и управляющей информации используются самые разнообразные устройства ввода информации. К ним относятся клавиатура; самые разнообразные манипуляторы - мышь, трэкбол, световое перо, джойстик; сканер; дигитайзер; системы речевого ввода и пр.
Клавиатура предназначена для ввода текстовой и управляющей информации. Она бывает мембранного, механического и полумеханического вида. Мышь предназначена для ввода управляющей информации. Графический редактор позволяет вводить с помощью мыши и графическую информацию. Световое перо также предназначено для ввода графической и управляющей информации, а джойстик - для ввода только управляющей информации. Сканер - это устройство для ввода графической информации, также как и дигитайзер. При наличии специальных программ оптического распознавания символов сканер можно использовать и для ввода текстовой информации. Сканеры бывают ручные, портативно-страничные и планшетные. В систему речевого ввода, предназначенного для ввода звуковой информации, входит микрофон, подключенный к устройствам оцифровки звука.
ЗАДАНИЕ 5
Нарисуйте свое “генеалогическое дерево” (можно перед этим рассмотреть родословные деревья А.С.Пушкина или царского дома Романовых). Не забудьте включить в модель бабушек и дедушек, братьев и сестер не только ваших, но и ваших родителей.
Попробуйте эту иерархическую структуру “перевести” (преобразовать, свести) в таблицу.
ЗАДАНИЕ 6
Модель объекта задана символьным описанием графа:
а(1,2) b(1,4) c(2,4) d(3,5) e(4,5) f(3.4)
Представьте ее в виде графического изображения и в табличном виде.
ОТВЕТ
Изображения графа могут быть разными, на рисунке 2.5.10 представлены два возможных.
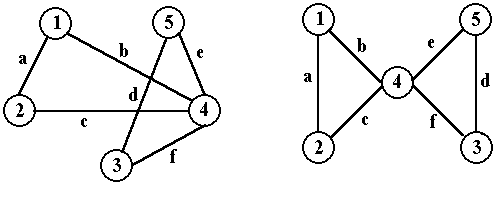
Рисунок 2.5.10.
Таблица:
|
| 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 | 1 |
| 4 | 1 | 1 | 1 | 0 | 1 |
| 5 | 0 | 0 | 1 | 1 | 0 |
ЗАДАНИЕ 6
Схему московского метрополитена можно рассматривать как граф. Выделите элементы этого графа и ответьте на вопросы: что является вершинами и ребрами графа? есть ли на этом графе дуги? является ли он взвешенным?
ЗАДАНИЕ 7
Один из методов сортировки (упорядочивания) числовых массивов данных так и называется - метод дерева. На первом этапе этого метода строится двоичное дерево исходного неупорядоченного массива. Строится оно следующим образом. Первый элемент массива рассматривается как корень дерева. Место вершины для каждого следующего элемента определяется так: спускаемся от корня (и далее от каждой промежуточной вершины) по левой ветке, если значение элемента меньше, чем вес этой вершины, и по правой ветке, если значение элемента больше.
Проверте, правильно ли построены деревья для двух неупорядоченных массивов, состоящих из одинаковых элементов, но расположенных в разном порядке. Определите, какие вершины являются корнем и листьями для каждого дерева.
Придумайте метод обхода таких деревьев, чтобы получить в результате упорядоченный массив тех же данных.
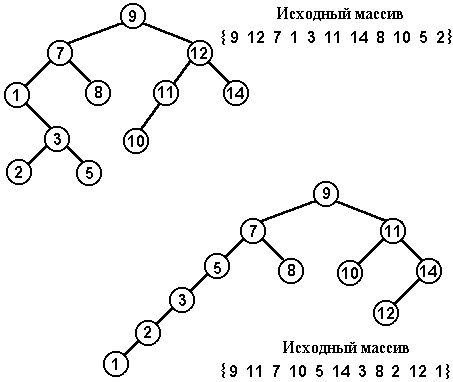
Рис. 5.2.11. “Деревья” неупорядоченных массивов
ЗАДАНИЕ 8
На рисунке 2.5.12 представлен фрагмент каталога диска. Для каждого файла выпишите полный путь к нему.
Путь к файлу - это имя устройства, на котором находится файл, и последовательный перечень подкаталогов, которые надо открыть, чтобы достичь заданный файл. Например, С:\ DOS \ UTILIT \ ndd.exe
Имена подкаталогов указаны прописными буквами, имена файлов - строчными.
C:

 DOC
DOC

 UTILIT
UTILIT

 ndd.exe
ndd.exe
 fformat.com
fformat.com

 SYSTEM
SYSTEM
 readme.txt
readme.txt
 proba.exe
proba.exe
 mif.sys
mif.sys
 MY_DOC
MY_DOC

 TEXT
TEXT

 PROZA
PROZA

 proza1.doc
proza1.doc
 proza2.doc
proza2.doc
 pismo1.doc
pismo1.doc

 RISUNKI
RISUNKI
 emblema.bmp
emblema.bmp
Рис. 2.5.12. Каталог диска (фрагмент)




















 DOC
DOC
 UTILIT
UTILIT
 SYSTEM
SYSTEM









