Презентации "Симметрия"

Выполнила:

ученица 8 класса

Сысенко Светлана

Что такое симметрия?

• Симметрия - (др.-греч. συμμετρία), в широком смысле — неизменность при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.

• Отсутствие или нарушение симметрии называется асимметрией.

Виды симметрий .

• Центральной симметрией относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA, в то время как обозначение SA можно перепутать с осевой симметрией.

• Осевая симметрия — тип симметрии, имеющий два несколько отличающихся определения:

• Отражательная симметрия. В математике (точнее, евклидовой геометрии) осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат.

• Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная, лучевая симметрии) относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но конус будет .
• Применительно к плоскости эти оба вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).
• Иногда вводят также (осевую) симметрию некоторого порядка:
• Осевая симметрия n-го порядка - симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси. Описывается группой Z n .
• Тогда симметрия в первом смысле (см. выше) является осевой симметрией второго порядка.

Симметрия в природе

• Симметрия в биологии  — это закономерное расположение подобных (одинаковых) частей тела или форм живого организма, совокупности живых организмов относительно центра или оси симметрии.
• Тип симметрии определяет не только общее строение тела, но и возможность развития систем органов животного. Строение тела многих многоклеточных организмов отражает определённые формы симметрии. Если тело животного можно мысленно разделить на две половины, правую и левую, то такую форму симметрии называют билатеральной . Этот тип симметрии свойственен подавляющему большинству видов, а также человеку. Если тело животного можно мысленно разделить не одной, а несколькими плоскостями симметрии на равные части, то такое животное называют радиально-симметричным . Этот тип симметрии встречается значительно реже.

Примеры симметрии

• Сложные узоры на крыльях бабочки являются одним из примеров двусторонней симметрии

СИММЕТРИЯ В МИРЕ РАСТЕНИЙ

• Для листьев характерна зеркальная симметрия. Эта же симметрия встречается и у цветов, однако у них зеркальная симметрия чаще выступает в сочетании с поворотной симметрией. Нередки случаи и переносной симметрии (веточки акации, рябины). Интересно, что в цветочном мире наиболее распространена поворотная симметрия 5-го порядка

СИММЕТРИЯ В МИРЕ ЖИВОТНЫХ

• Хотя внешняя спиральная симметрия у многоклеточных животных встречается редко, зато спиральную структуру имеют многие важные молекулы, из которых построены живые организмы – белки, дезоксирибонуклеиновые кислоты – ДНК4.

Симметрия в минералах

• Если же кристалл можно разделить на две части таким образом, что одна служит зеркальным отображением другой, то плоскость раздела будет плоскостью симметрии. В1 кристаллах кроме осей и плоскостей симметрии может быть и центр симметрии, в диаметрально противоположных направлениях от которого расположены одинаковые элементы огранки кристалла (грани, ребра, вершины). К этому можно добавить, что центр симметрии делит пополам любую проведенную через него прямую линию.

Другие примеры….

• Соты - настоящий конструкторский шедевр. Они состоят из ряда симметричных шестигранных ячеек .

• очертания снежной кристаллической звездочки

Параллельный перенос в пространстве.

Работу выполнила

ученица 10 класса

Подпрядова Кристина.

ЦЕЛЬ РАБОТЫ: РАССМОТРЕТЬ ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС В ПРОСТРАНСТВЕ.

ЗАДАЧИ: 1)ДАТЬ ОПРЕДЕЛЕНИЕ ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА,

2) П РИВЕСТИ ПРИМЕРЫ.

Определение.

Параллельный перенос пространства перемещает все точки в одном и том же направлении на одно и то же расстояние.

Параллельный перенос в разных областях науки.

• Параллельное перенесение  — обобщение понятия «параллельный перенос» на случай искривлённых пространств.
• Поступательное движение  — движение в  механике , разница положений при котором в любые 2 момента времени представляет собой параллельный перенос.
• Трансляция (кристаллография)
• Трансляционная симметрия

СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА .

Две различные точки и их образы, полученные параллельным переносом, являются вершинами параллелограмма , в котором отрезок, соединяющий две начальные точки, образует одну сторону, а отрезок, соединяющий два их образа — противоположную ей сторону.

У параллельного переноса нет  неподвижных точек , но имеются инвариантные  прямые . [2]

Совокупность всех параллельных переносов образует  группу , которая в  евклидовом пространстве  является нормальной подгруппой  группы движений, а в  аффинном  ― нормальной подгруппой группы  аффинных преобразований .

Примеры из жизни.

В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве.

А также, параллельный перенос можно встретить и в таких необычных ситуациях:

В ходе выполнения своей работы я познакомилась:

• с параллельным переносом в пространстве,
• с параллельным переносом в разных областях науки,
• со свойствами параллельного переноса,

- примерами параллельного переноса в жизни.

Интернет источники:

https:// ru.wikipedia.org/wiki/

edu.sernam.ru

artoil-a.narod.ru

Симметрия в математике

Выполнила:

Ученица 10 класса

Сысенко Светлана

Типы симметрии

Осевая симметрия:

Вращательная

Зеркальная

Центральная симметрия

Осевая симметрия

• осевая симметрия – это симметрия относительно оси.

Зеркальная симметрия

• Геометрическая фигура называется симметричной относительно плоскости S (рис.1), если для каждой точки E этой фигуры может быть найдена точка E’ этой же фигуры, так что отрезок EE’ перпендикулярен плоскости S и делится этой плоскостью пополам ( EA = AE’ ). Плоскость S называется плоскостью симметрии. Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова ( например, левая перчатка не подходит для правой руки и наоборот ). Они называются зеркально равными.

Равнобедренный треугольник с зеркальной симметрией. Пунктирная линия является осью симметрии.

Круглый конус обладает осевой симметрией; ось симметрии – ось конуса

• Равнобокая трапеция имеет осевую симметрию. Её ось симметрии – перпендикуляр, проведенный через середины оснований трапеции

• Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними

Так же примерами зеркальной симметрии являются равенства:

• 2+3=3+2
• 7+3=3+7
• 11+4=4+11

и т. п.

Вращательная симметрия

• Вращательная симметрия — термин, означающий симметрию объекта относительно всех или некоторых собственных вращений m-мерного евклидова пространства.

Центральная симметрия

• Геометрическая фигура

( или тело ) называется симметричной относительно центра C (рис.2), если для каждой точки A этой фигуры может быть найдена точка E этой же фигуры, так что отрезок AE проходит через центр C и делится в этой точке пополам (AC = CE). Точка C называется центром симметрии.

Центральная симметрия равностороннего треугольника

Центральная симметрия квадрата

Параллелограмм имеет центральную симметрию. Его центр симметрии – точка пересечения диагоналей

• Шар ( сфера ) обладает и центральной, и зеркальной, и симметрией вращения. Центром симметрии является центр шара; плоскостью симметрии является плоскость любого большого круга; осью симметрии – диаметр шара.

• Ромб имеет и центральную, и осевую симметрию. Его ось симметрии – любая из его диагоналей; центр симметрии – точка их пересечения

Равнобедренный треугольник

Равнобедренный треугольник имеет одну ось симметрии.

Прямоугольник

Прямоугольник имеет две оси симметрии.

Ромб

Ромб имеет две оси симметрии .

Равносторонний треугольник

Равносторонний треугольник имеет три оси симметрии.

Квадрат

Квадрат имеет четыре оси симметрии .

Круг

Окружность имеет бесконечно много осей симметрии. Это любые прямые, проходящие через ее центр.

Спасибо за внимание!

Симметрия в технике

Выполнили работу

ученики 10 класса

Ядрышников Денис и сидоров Александр

Учитель Семина Лилия Анатольевна

Проблема: может ли техника существовать без симметрии?

Цель исследования:

• Целесообразность симметрии технике

Задачи:

• Показать роль симметрии в технике.
• Показать пользу симметрии в технике.

Глядя на транспортные средства, мы задали себе вопрос:

Чем объясняется частое присутствие симметрии в технике?

Изучив необходимую литературу, поняли, что симметрия, прежде всего, определяется целесообразностью.

Никому не нужен кривой автомобиль или самолёт с крыльями разной длины. Кроме того симметричные объекты красивы.

Технические объекты – самолёты, автомашины, ракеты, молотки, гайки – практически все они от мала до велика обладают той или иной симметрией. Случайно ли это? ,

В технике красота, соразмерность механизмов часто бывает связана с их надёжностью, устойчивостью в работе

Симметричная форма дирижабля, самолёта, подводной лодки, автомобиля и т.д. обеспечивает хорошую обтекаемость воздухом или водой, а значит, и минимальное сопротивление движению.

На заре развития авиации наши знаменитые учёные Н. Е. Жуковский и С. А. Чаплыгин исследовали полёт птиц, чтобы сделать выводы относительно наивыгоднейшей формы крыла и условий его полёта.

Большую роль в этом сыграла, конечно, симметрия.

В ходе выполнения своей работы мы поняли,

что техника не может существовать без симметрии.

Целесообразность симметрии в том, что без нее техника была бы не пригодна для использования.

Интернет ресурсы

https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F#. D0.A1.D1.81.D1.8B.D0.BB.D0.BA.D0.B8 -википедия

http:// nsportal.ru/ap/library/drugoe/2013/10/07/prezentatsiya-simmetriya-v-tekhnike - симметрия в технике

http://www.myshared.ru/slide/204963 / - симметрия

https:// www.google.ru/search?q - картинки

Коллекция картинок Microsoft Office.

Спасибо за внимание

Движение в пространстве

Работу выполнили:

Кузеванова Екатерина, ученица 10 класса

Пеканова Виктория, ученица 10 класса.

Руководитель:

Семина Лилия Анатольевна,

учитель физики и математики.

Цель: Определить, что происходит при движении в пространстве.

Задачи:

• Узнать, что такое движение в пространстве;

• Определить свойства движения в пространстве;

• Узнать как ведут себя неподвижные точки движений пространства;

4. Определить виды движения в пространстве;

Объект исследования: Движение в пространстве.

Метод исследования: Поиск, обработка информации

Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|.

Движением называется преобразование, при котором сохраняются расстояния между точками.

Свойства:

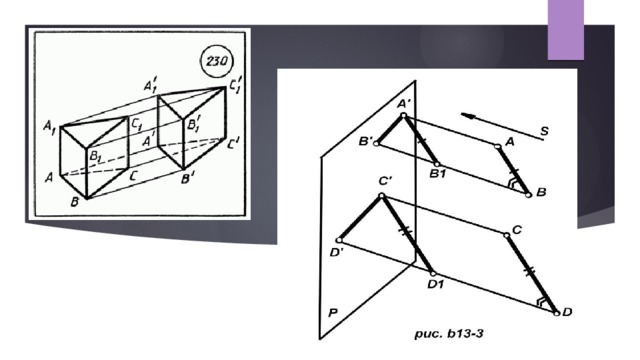
• При движении в пространстве прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, плоскости – в плоскости; сохраняются углы между полупрямыми.

• Две фигуры называются равными , если они совмещаются движением.

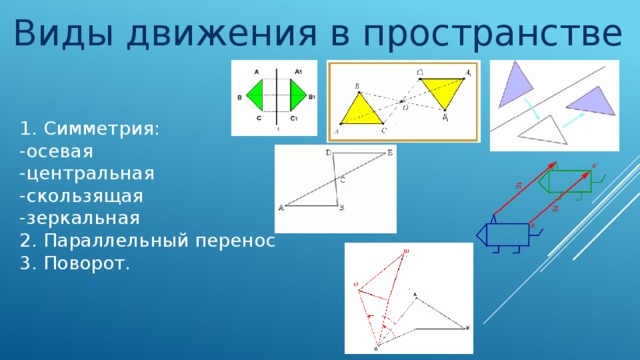
Виды движения в пространстве

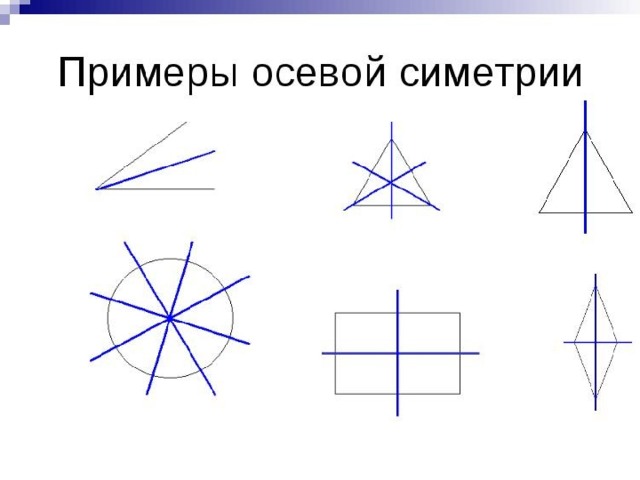
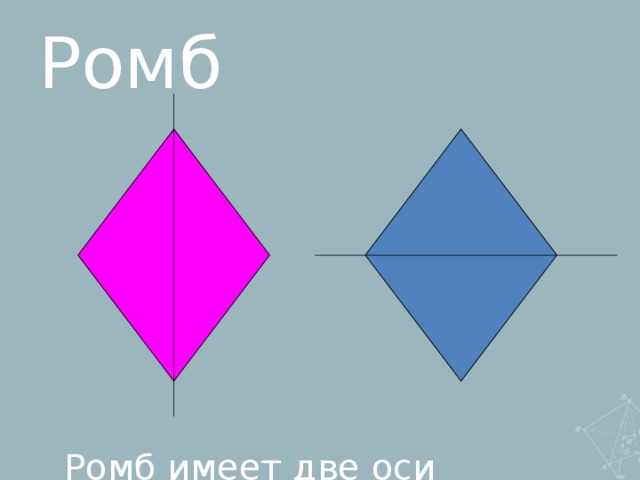
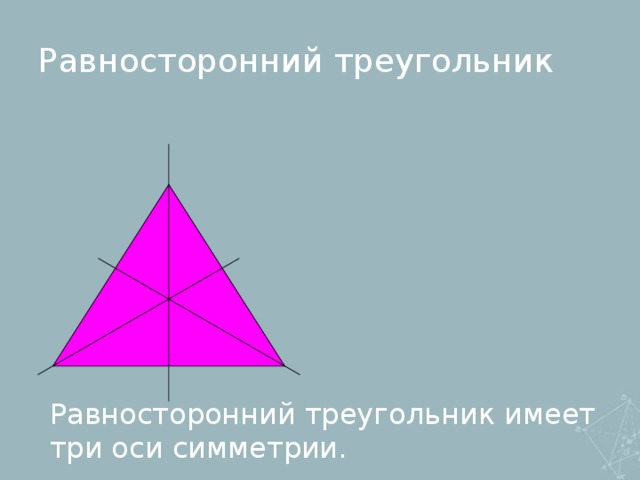
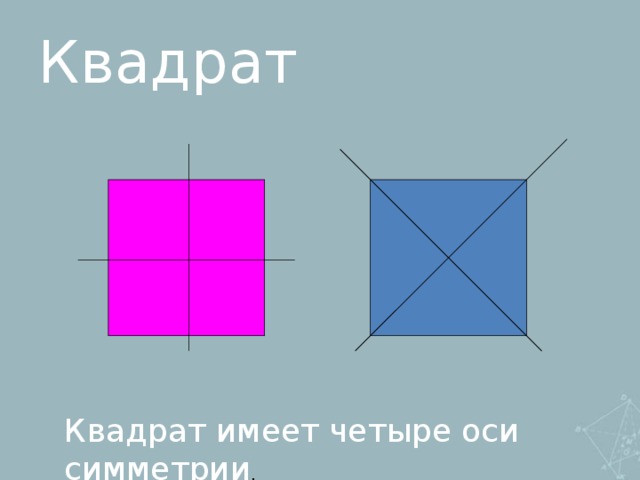
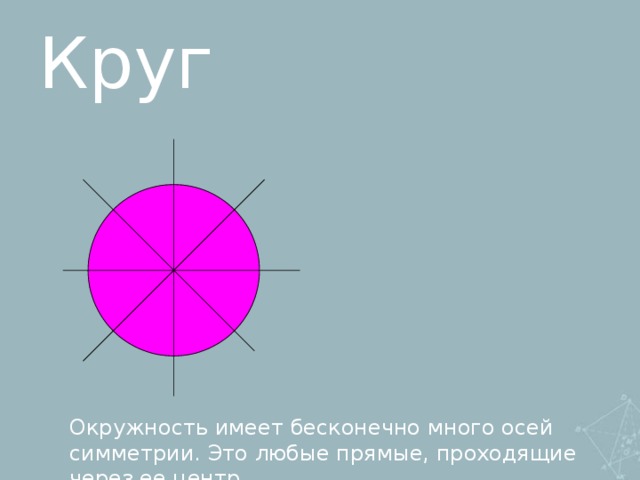
1. Симметрия:

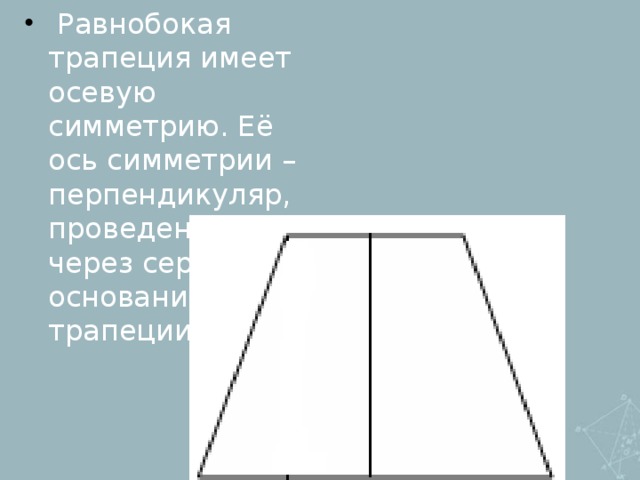
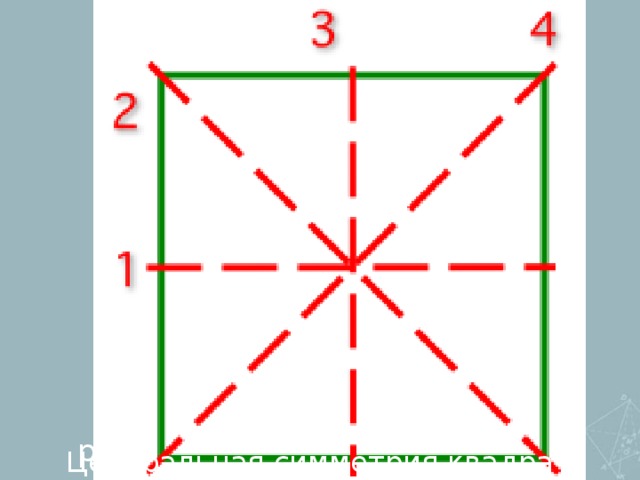
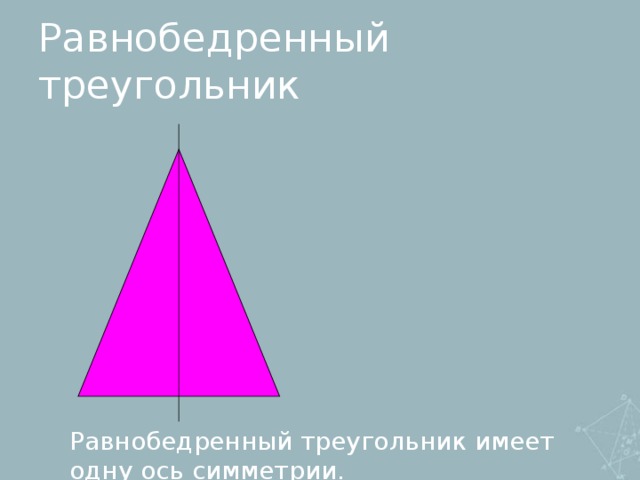
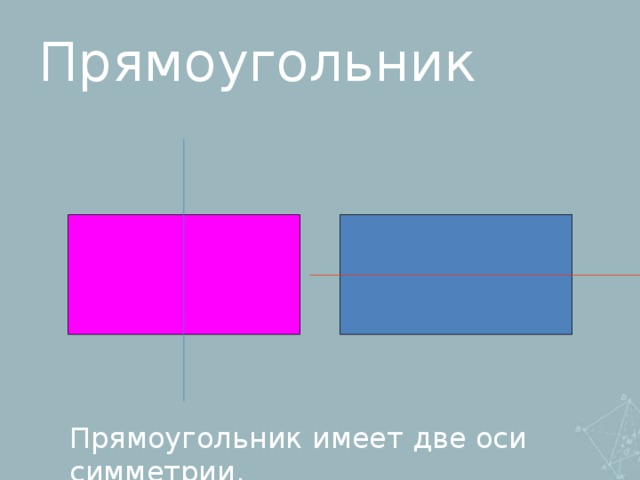
-осевая

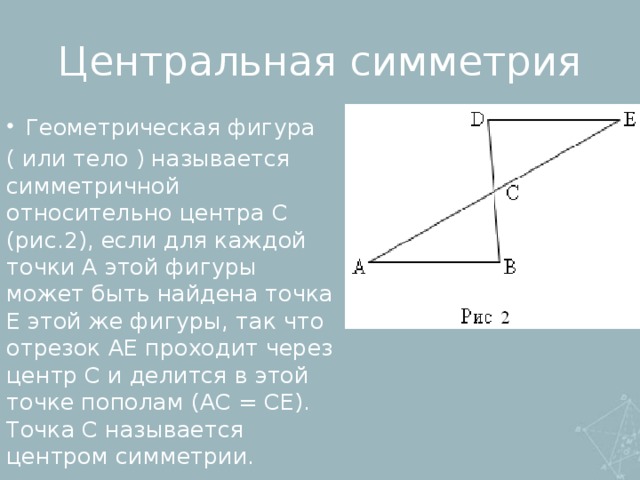
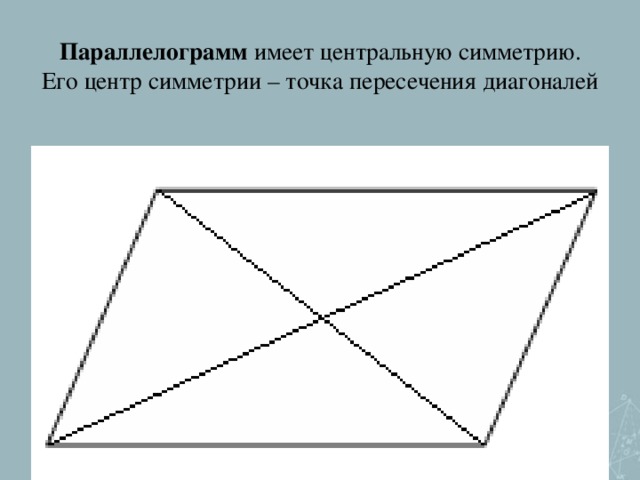
-центральная

-скользящая

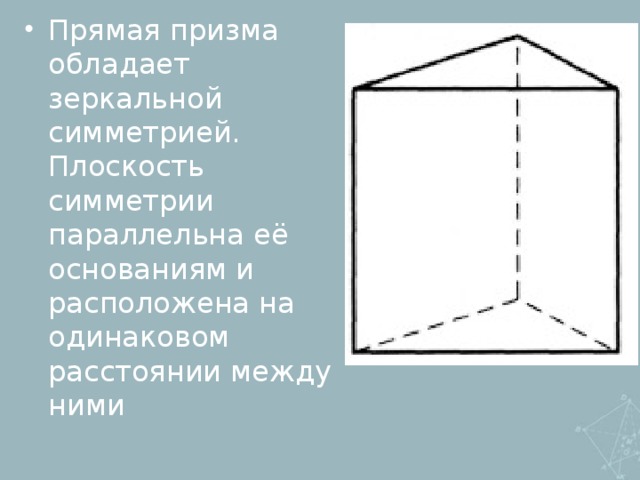
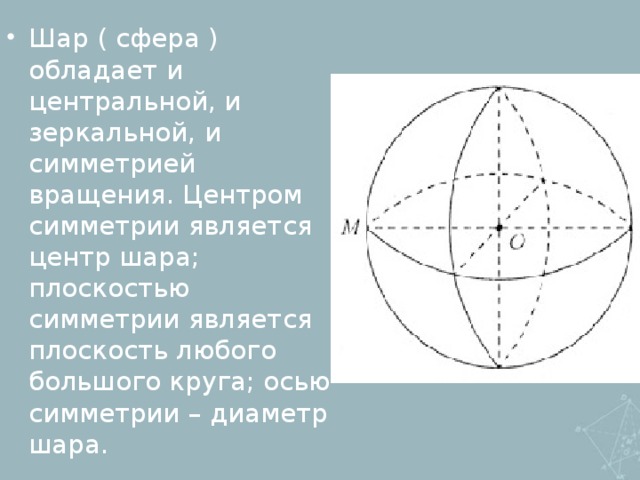
-зеркальная

2. Параллельный перенос

3. Поворот.

Неподвижные точки движений пространства.

Важной характеристикой движения пространства является множество его неподвижных точек. Здесь могут представиться лишь следующие пять случаев:

1.У движения неподвижных точек нет (нетождественный параллельный перенос).

2.Движение имеет лишь одну неподвижную точку (центральная симметрия).

3.Множество неподвижных точек движения пространства является прямой (поворот вокруг прямой).

4.Множество неподвижных точек движения пространства является плоскостью (зеркальная симметрия).

5.Множество неподвижных точек движения пространства является всем пространством (тождественное движение).

Вывод

Работая над проектом, мы узнали, что же происходит при движении в пространстве:

- прямые переходят в прямые,

- полупрямые — в полупрямые,

- отрезки — в отрезки,

- сохраняются углы между прямыми .

Источники информации:

http:// nsportal.ru/shkola/geometriya/library/2015/03/07/prezentatsiya-obuchayushchikhsya-10-klassa-po-geometrii-na-temu

http:// www.yaklass.ru/p/geometria/11-klass/metod-koordinat-v-prostranstve-dvizheniia-10439/dvizheniia-12444/re-173fee54-d497-47c1-82e1-e1a0a0d883e2

https://www.google.ru/url?sa=i&rct=j&q=&esrc=s&source=images&cd=& cad=rja&uact=8&ved=0ahUKEwjHgpSR5uzLAhUGlCwKHaG0AcUQjhwIBQ&url=http%3A%2F%2Fpinedbaud.blogspot.com%2F2012%2F12%2Fblog

www.likt590.ru

geometry-and-art.ru

znaika.ru

Симметрия в технике

Симметрия – символ красоты, гармонии и совершенства.

Выполнил: ученик Хамзин Максим

В древности слово симметрия”употреблялась как “красота”, “гармония”. Термин “гармония” в переводе с греческого означает “соразмерность, одинаковость в расположении частей”. Известный немецкий математик Герман Вейль дал определение симметрии таким образом: “Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство”.

Симме́три́я в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях (например: положения, энергии, информации, другого). Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.

Центральная симметрия

Зеркальная симметрия

Осевая симметрия

Экспериментально

право-левая симметрия

в мире элементарных частиц

была обнаружена в 1956 г.

Она выражалась в том,

что при распаде ядра

кобальта электроны летят

"вниз" чаще, чем "вверх"

Радиальная или лучевая симметрия

Детали с разными видами симметрий

Через любую плоскую круглую и шарообразную форму можно провести как минимум две симметрии.

Асимметрия – обратная симметрии.

Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность. Итак, "сфера влияния" симметрии (а значит, ее антипода - асимметрии), поистине безгранична.

Природа - наука - искусство. Всюду мы видим противоборство, а часто и единство двух великих начал - симметрии и асимметрии, которые во многом и определяют гармонию природы, мудрость науки и красоту искусства.

Вывод

Симметрия – это не только математическое понятие. Его заимствовали из природы.

А так как человек – это часть природы, то человеческое творчество во всех его проявлениях тяготеет к симметрии.

Симметрия в живой природе: в животном и растительном мире, – передается генетически из поколения в поколение. На вопрос: “Есть ли будущее без симметрии?” мы можем ответить словами классика современного естествознания, мыслителя Владимира Ивановича Вернадского: “Принцип симметрии охватывает все новые и новые области…”.