Презентация "Геометрические построения"

ГЕОМЕТРИЧЕСКИЕ

ПОСТРОЕНИЯ

Выполнила учитель черчения

Анисимова Н.В.

Тема занятия: «Простейшие геометрические построения: деление отрезков, углов и окружностей на равные части. Нахождение центра дуги»

Цель занятия:

Образовательная: - приобщение учащихся к графической культуре, освоение правил и приемов выполнения геометрических построений с помощью чертежных инструментов; расширить знания обучающихся о способах геометрических построений, применяемые при выполнении чертежей деталей, изделий. Развивающая: - овладение учащимися графического языка техники и способность применять полученные знания для решения практических и графических задач с творческим содержанием ; формирование навыков работы чертёжным инструментом; самоконтроля при выполнение геометрических построений. Развивать у обучающихся глазомер, аккуратность при выполнении работы. Воспитательная: - воспитывать культуры труда, аккуратность, внимательность, трудолюбие, творческое отношение к труду; формирование навыков самостоятельной работы .

Выполнение графических работ с помощью чертёжных инструментов:

- деление отрезка на равные части;

- деление угла и дуги на равные части;

- деление окружностей на равные части;

- нахождение центра дуги;

- создание орнамента.

½ AB R 1 = R 2 ∟ AOC =90° [AO]=[OB] " width="640"

R 1

R 2

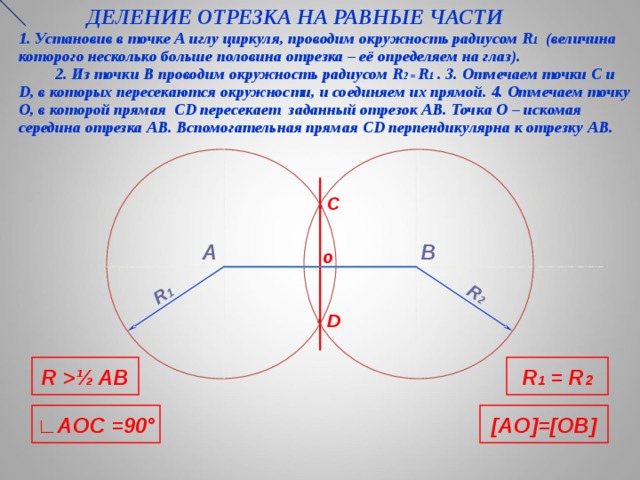
ДЕЛЕНИЕ ОТРЕЗКА НА РАВНЫЕ ЧАСТИ 1. Установив в точке А иглу циркуля, проводим окружность радиусом R 1 ( величина которого несколько больше половина отрезка – её определяем на глаз). 2. Из точки В проводим окружность радиусом R 2 = R 1 . 3. Отмечаем точки C и D , в которых пересекаются окружности, и соединяем их прямой. 4. Отмечаем точку О, в которой прямая CD пересекает заданный отрезок АВ. Точка О – искомая середина отрезка АВ. Вспомогательная прямая CD перпендикулярна к отрезку АВ.

С

•

В

А

o

D

•

R ½ AB

R 1 = R 2

∟ AOC =90°

[AO]=[OB]

R 1

R 3

R 2

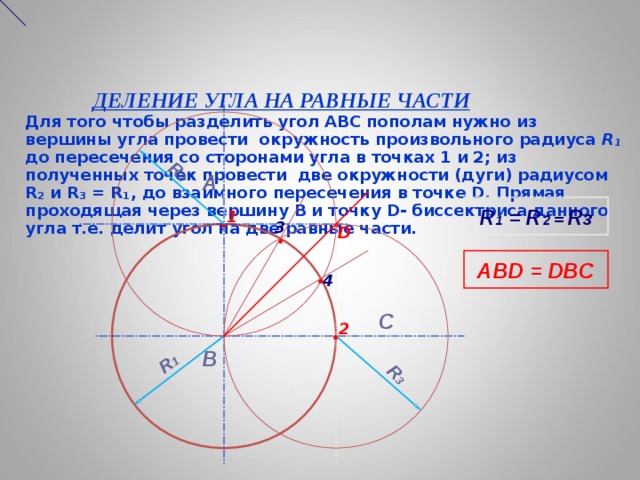
ДЕЛЕНИЕ УГЛА НА РАВНЫЕ ЧАСТИ Для того чтобы разделить угол АВС пополам нужно из вершины угла провести окружность произвольного радиуса R ₁ до пересечения со сторонами угла в точках 1 и 2; из полученных точек провести две окружности (дуги) радиусом R ₂ и R₃ = R₁ , до взаимного пересечения в точке D. Прямая проходящая через вершину В и точку D- биссектриса данного угла т.е. делит угол на две равные части.

А

R 1 = R 2 = R 3

1

•

•

3

D

•

ABD = DBC

•

4

С

2

•

В

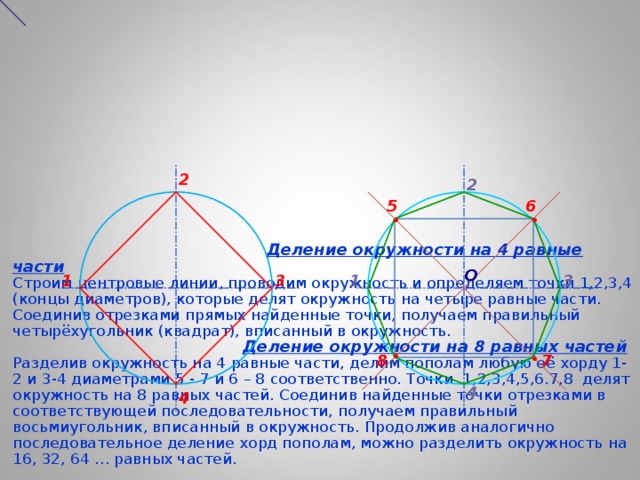
Деление окружности на 4 равные части Строим центровые линии, проводим окружность и определяем точки 1,2,3,4 (концы диаметров), которые делят окружность на четыре равные части. Соединив отрезками прямых найденные точки, получаем правильный четырёхугольник (квадрат), вписанный в окружность. Деление окружности на 8 равных частей Разделив окружность на 4 равные части, делим пополам любую её хорду 1-2 и 3-4 диаметрами 5 - 7 и 6 – 8 соответственно. Точки 1,2,3,4,5,6.7,8 делят окружность на 8 равных частей. Соединив найденные точки отрезками в соответствующей последовательности, получаем правильный восьмиугольник, вписанный в окружность. Продолжив аналогично последовательное деление хорд пополам, можно разделить окружность на 16, 32, 64 … равных частей.

2

2

6

5

•

•

О

3

3

1

1

•

•

7

8

4

4

Деление окружности на 4 и 8 равных частей с помощью циркуля и треугольника с углами 90 ⁰х45⁰х45 ⁰

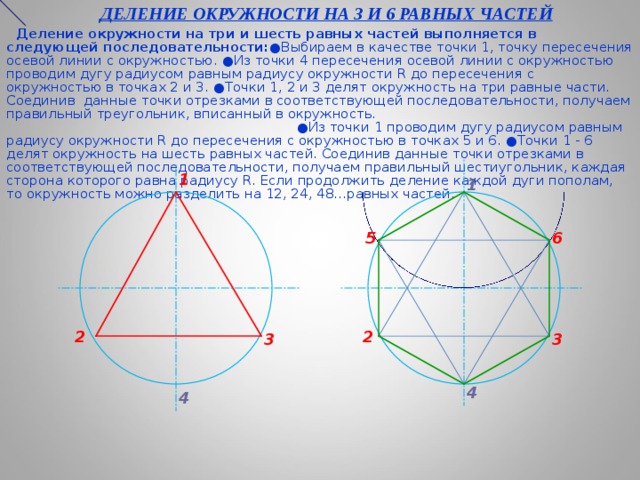
ДЕЛЕНИЕ ОКРУЖНОСТИ НА 3 И 6 РАВНЫХ ЧАСТЕЙ

Деление окружности на три и шесть равных частей выполняется в следующей последовательности: ● Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью. ● Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3. ● Точки 1, 2 и 3 делят окружность на три равные части. Соединив данные точки отрезками в соответствующей последовательности, получаем правильный треугольник, вписанный в окружность. ● Из точки 1 проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6. ● Точки 1 - 6 делят окружность на шесть равных частей. Соединив данные точки отрезками в соответствующей последовательности, получаем правильный шестиугольник, каждая сторона которого равна радиусу R. Если продолжить деление каждой дуги пополам, то окружность можно разделить на 12, 24, 48…равных частей.

1

1

6

5

2

2

3

3

4

4

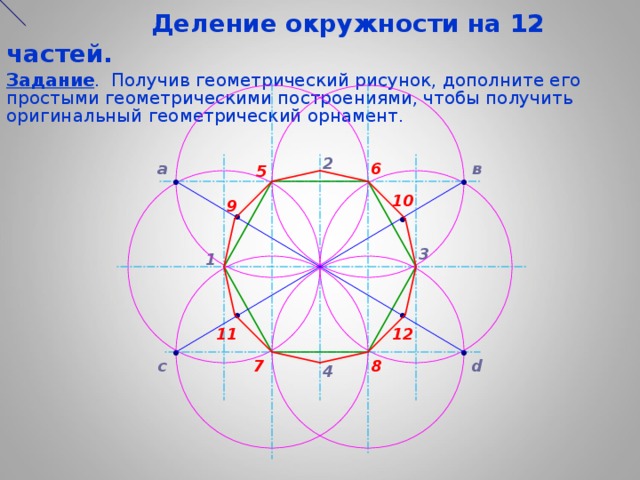
Деление окружности на 12 частей.

Задание . Получив геометрический рисунок, дополните его простыми геометрическими построениями, чтобы получить оригинальный геометрический орнамент.

2

6

а

в

5

•

•

10

9

•

•

3

1

•

•

12

11

•

•

с

d

8

7

4

Деление окружности на 3 равные части с помощью циркуля, угольника и линейки

Деление окружности на 6 равных частей с помощью циркуля, угольника и линейки

Деление окружности на 12 равных частей с помощью угольника и линейки

ДЕЛЕНИЕ ОКРУЖНОСТИ НА 5 РАВНЫХ ЧАСТЕЙ

Деление окружности на 5 равных частей выполняется в следующей последовательности: 1) делим радиус ОВ пополам (точка С); 2) радиусом С - 1проводим окружность (дугу) до пересечения с окружностью, получаем точки 2, 3; 3) из точек 2, 3 этим же радиусом проводим соответственно окружности (дуги) до пересечения с окружностью, получаем точки 4, 5; 4) Соединив точки 1 - 3; 3 - 4; 4 - 5; 5 - 2 и 2 - 1 отрезками получаем правильный пятиугольник

R

1

2

•

•

3

B

•

O

C

•

•

4

5

C = ½( OB)

R = ( C – 1 )

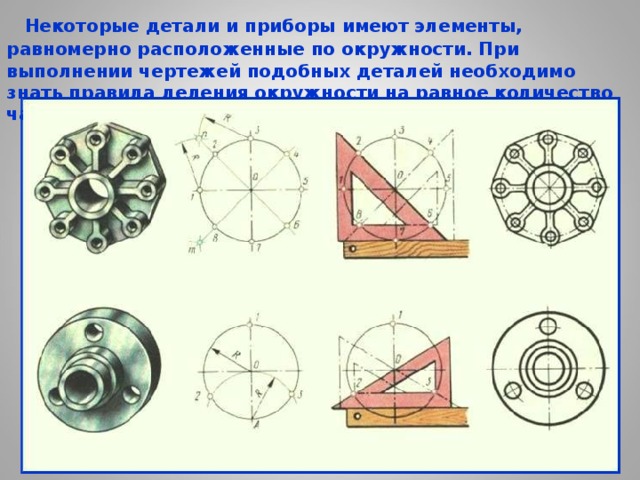
Некоторые детали и приборы имеют элементы, равномерно расположенные по окружности. При выполнении чертежей подобных деталей необходимо знать правила деления окружности на равное количество частей

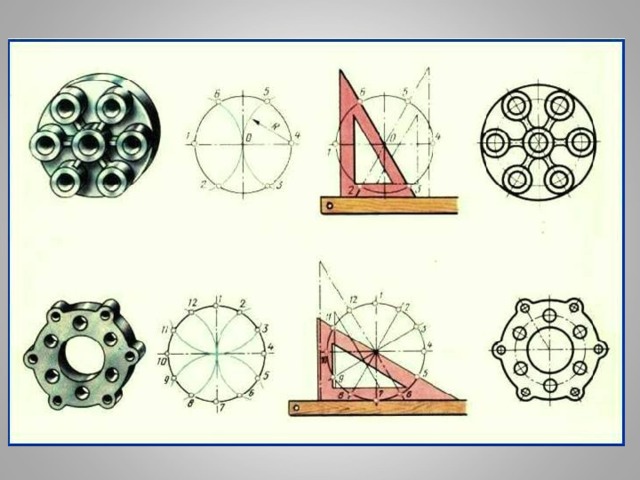
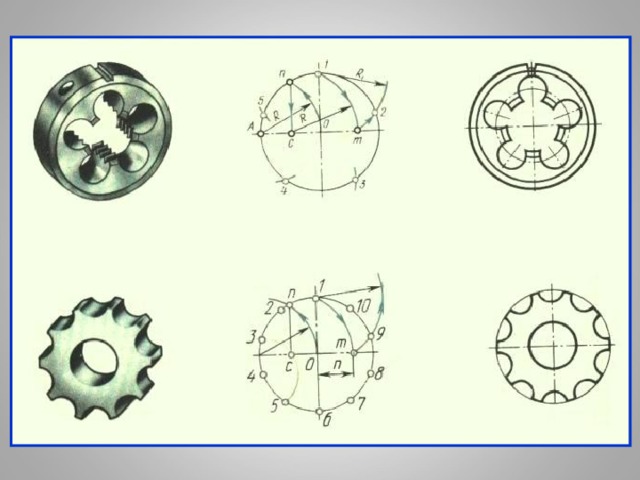
Опорные термины

Отрезок, параллельные линии, перпендикуляр, угол, биссектриса, дуга, радиус, диаметр, окружность, хорда, орнамент

Информационные источники и ЭОР

Учебники:

1. Ботвинников А.Д.Черчение 7-8 – М: «Просвещение», 2005.

2. Гордеенко Н.А. Черчение 9 класс – М: АСТ, 2007.

3. А.А. Павлова, Е.И. Корзинова. Черчение и графика. 8 – 9 классы : М. : Мнемозина, 2007

4. Степакова В.В. Методическое пособие по черчению – М: «Просвещение», 2004

5. С.К. Боголюбов. Черчение. М: «Машиностроение», 1085.

myshared.ru › slide/451366/

900igr.net › prezentatsii/ geometrija

5klass.net ;

myshared.ru ›

slide/605578 /