
Математический бой
Внеклассное мероприятие для 11 класса

Список задач
- Задача 1
- Задача 2
- Задача 3
- Задача 4
- Задача 5
- Задача 6
- Задача 7
- Задача 8
- Задача 9
- Задача 10
- Задача 11
- Задача 12

Задача 1
- Проверить решение
- Вернуться к выбору задачи
Система навигации, встроенная в спинку самолетного кресла, информирует пассажира о том, что полет проходит на высоте 37 170 футов. Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.

Задача 1
- Решение задачи
- Переведем высоту из футов в сантиметры: 37 170 30,5 = 1 133 685 см. Переведем высоту из сантиметров в метры: 1 133 685 : 100 = 11 336,85 м. Следовательно, полет проходит на высоте 11 336,85 метра.
- Ответ: 11 336,85.
- Вернуться к выбору задачи
Система навигации, встроенная в спинку самолетного кресла, информирует пассажира о том, что полет проходит на высоте 37 170 футов. Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
Задача 2
- Проверить решение
- Вернуться к выбору задачи
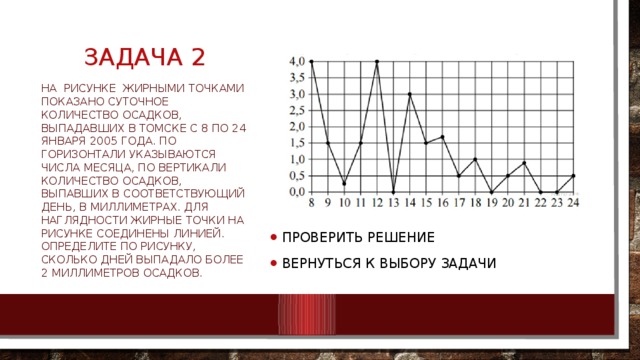
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков.

Задача 2
- Решение задачи
- Видно, что более 2 миллиметров осадков выпадало три дня: 8, 12 и 14 января (см. рис.).
- Ответ: 3.
- вернуться к выбору задачи
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков.

Задача 3
- Проверить решение
- Вернуться к выбору задачи
Найдите ординату середины отрезка, соединяющего точки O(0; 0) и A(6; 8).

Задача 3
- Решение задачи
- Координаты точки, делящей отрезок пополам , считаются по формуле:
- Ответ: 4.
- Вернуться к выбору задачи
Найдите ординату середины отрезка, соединяющего точки O(0; 0) и A(6; 8).

Задача 4
- Проверить решение
- Вернуться к выбору задачи
Вероятность того, что на тестировании по математике учащийся П. верно решит больше 12 задач, равна 0,7. Вероятность того, что П. верно решит больше 11 задач, равна 0,79. Найдите вероятность того, что П. верно решит ровно 12 задач.

Задача 4
- Решение задачи
- Рассмотрим события A = «учащийся решит 12 задач» и В = «учащийся решит больше 12 задач». Их сумма - событие A + B = «учащийся решит больше 11 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
- P(A + B) = P(A) + P(B).
- Тогда, используя данные задачи, получаем: 0,79 = P(A) + 0,7, откуда P(A) = 0,79 − 0,7 = 0,09.
- Ответ: 0,09.
- Вернуться к выбору задачи
Вероятность того, что на тестировании по математике учащийся П. верно решит больше 12 задач, равна 0,7. Вероятность того, что П. верно решит больше 11 задач, равна 0,79. Найдите вероятность того, что П. верно решит ровно 12 задач.

Задача 5
- Проверить решение
- Вернуться к выбору задачи
Решите уравнение

Задача 5
- Решение задачи
- Выполним преобразования, используя формулы
- Ответ: х=1,5
- Вернуться к выбору задачи
Решите уравнение
Задача 6
- Проверить решение
- Вернуться к выбору задачи
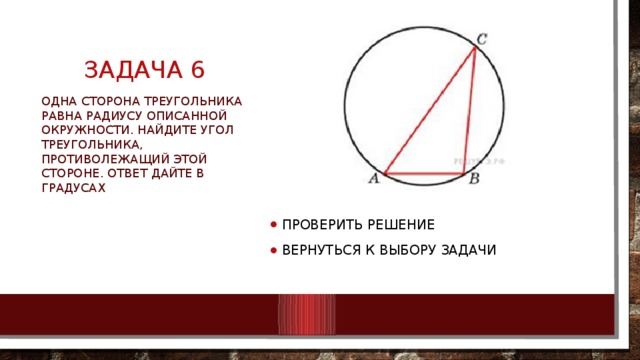
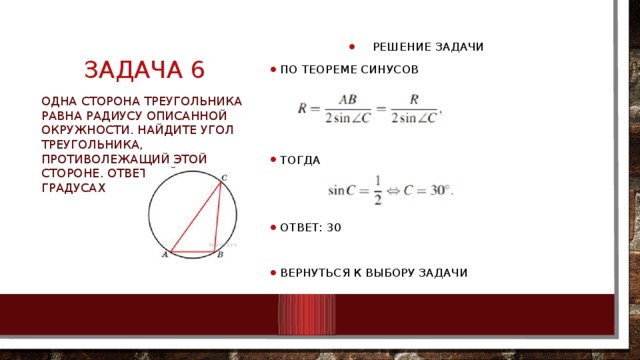
Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах
Задача 6
- Решение задачи
- По теореме синусов
- Вернуться к выбору задачи
Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах
Задача 7
- Проверить решение
- Вернуться к выбору задачи
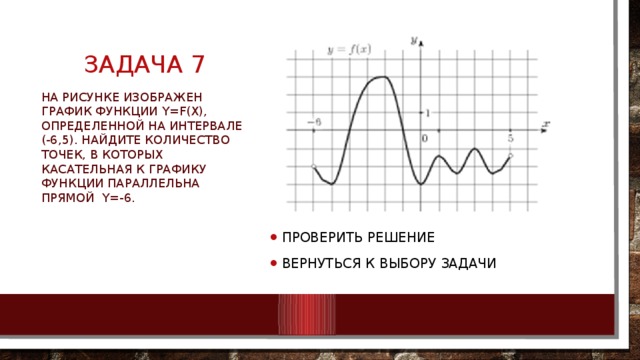
На рисунке изображен график функции y=f(x), определенной на интервале (-6,5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=-6.

Задача 7
- Решение задачи
- Поскольку касательная параллельна прямой y = −6 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. Производная равна нулю в точках экстремума функции. На заданном интервале функция имеет 3 максимума и 4 минимума, итого 7 экстремумов. Таким образом, касательная к графику функции параллельна прямой y = −6 или совпадает с ней в 7 точках.
- Ответ: 7.
- Вернуться к выбору задачи
На рисунке изображен график функции y=f(x), определенной на интервале (-6,5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=-6.
Задача 8
- Проверить решение
- Вернуться к выбору задачи
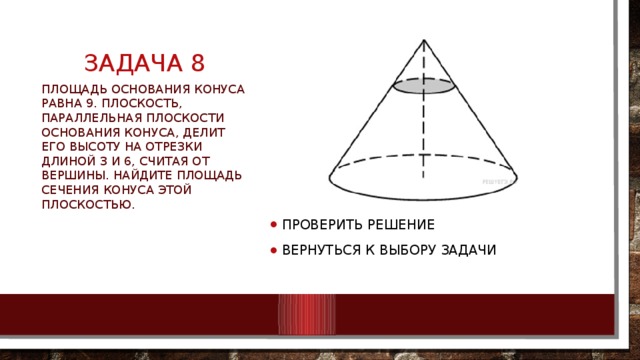
Площадь основания конуса равна 9. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Задача 8
- Решение задачи
- Сечение плоскостью, параллельной основанию, представляет собой круг, радиус которого относится к радиусу основания конуса как 3 : 9. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому площадь сечения в 9 раз меньше площади основания. Тем самым, она равна 1.
- Ответ: 1.
- Вернуться к выбору задачи
Площадь основания конуса равна 9. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Задача 9
- Проверить решение
- Вернуться к выбору задачи
Найдите значение выражения ,
Если

Задача 9
- Решение задачи
- Выполним преобразования:
- Ответ:12
- Вернуться к выбору задачи
Найдите значение выражения ,
Если

Задача 10
- Проверить решение
- Вернуться к выбору задачи
Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью v=3,6 м/с под острым углом α к рельсам. От толчка платформа начинает ехать со скоростью
где м=70 кг – масса скейтбордиста со скейтом, а М =350кг – масса платформы. Под каким максимальным углом нужно прыгать, чтобы разогнать платформу не менее чем до 0,3 м/с?

Задача 10
- Решение задачи
- Задача сводится к решению неравенства
- на интервале (0,90)
- Ответ: 60
- Вернуться к выбору задачи
Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью v=3,6 м/с под острым углом α к рельсам. От толчка платформа начинает ехать со скоростью
где м=70 кг – масса скейтбордиста со скейтом, а М =350кг – масса платформы. Под каким максимальным углом нужно прыгать, чтобы разогнать платформу не менее чем до 0,3 м/с?

Задача 11
- Проверить решение
- Вернуться к выбору задачи
Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Задача 11
- Решение задачи
- Пусть масса первого сплава m кг, а масса второго —(250-m) кг. Тогда массовое содержание никеля в первом и втором сплавах 0,1m и 0,35(250-m) соответственно. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. Получаем уравнение:
- Следовательно, масса второго сплава 150 кг. Разность масс — 50 кг
- Ответ:50
- Вернуться к выбору задачи
Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
![Задача 12 Проверить решение Вернуться к выбору задачи Найдите наименьшее значение функции на отрезке [-2; 5]](https://fsd.multiurok.ru/html/2017/12/10/s_5a2d5565c53d2/img24.jpg)
Задача 12
- Проверить решение
- Вернуться к выбору задачи
Найдите наименьшее значение функции
на отрезке [-2; 5]
![Решение задачи Найдем производную заданной функции: Задача 12 Найдем нули производной на заданном отрезке: В точке х =0 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение: Ответ: -18 Вернуться к выбору задачи Найдите наименьшее значение функции на отрезке [-2; 5]](https://fsd.multiurok.ru/html/2017/12/10/s_5a2d5565c53d2/img25.jpg)
- Решение задачи
- Найдем производную заданной функции:
Задача 12
- Найдем нули производной на заданном отрезке:
- В точке х =0 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
- Ответ: -18
- Вернуться к выбору задачи
Найдите наименьшее значение функции
на отрезке [-2; 5]





























![Задача 12 Проверить решение Вернуться к выбору задачи Найдите наименьшее значение функции на отрезке [-2; 5]](https://fsd.multiurok.ru/html/2017/12/10/s_5a2d5565c53d2/img24.jpg)
![Решение задачи Найдем производную заданной функции: Задача 12 Найдем нули производной на заданном отрезке: В точке х =0 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение: Ответ: -18 Вернуться к выбору задачи Найдите наименьшее значение функции на отрезке [-2; 5]](https://fsd.multiurok.ru/html/2017/12/10/s_5a2d5565c53d2/img25.jpg)










