Презентация к урокам по теме "Сечения"

Содержание

Введение ………………………………………………………..3

Историческая справка……………………………………..4

Многогранники………………………………………………..7

Сечения …………………………………………………………14

Методы построения сечений многогранников….26

Практическое применение………………………………40

Тест……………………………………………………………….41

Задачи…………………………………………………………..49

Заключение……………………………………………………61

Список используемой литературы…………………..62

Задачи на построение сечений многогранников занимают значительное место как в школьном курсе геометрии для старших классов, так и на экзаменах разного уровня. Решение этого вида задач способствует усвоению аксиом стереометрии, систематизации знаний и умений, развитию пространственного представления и конструктивных навыков. Общеизвестны трудности, возникающие при решении задач на построение сечений. Таким образом, целью данной работы является более глубокое изучение методов построения сечений и выявление наиболее рациональных из них.

Еще в глубокой древности человек чертил и рисовал на скалах, камнях, стенах и предметах домашнего обихода изображения вещей, деревьев, животных и людей. Он делал это для удовлетворения своих потребностей, в том числе эстетических. При этом основное требование к таким изображениям заключалось в том, чтобы изображение вызывало правильное зрительное представление о форме изображаемого предмета.

С ростом практических и технических применений изображений к ним стали предъявлять и такие требования, чтобы по изображению можно было судить о геометрических свойствах, размерах и взаиморасположении отдельных элементов определенного предмета. О таких требованиях можно судить по многим памятникам древности, уцелевшим до наших дней. Однако строгие геометрические обоснованные правила и методы изображения пространственных фигур стали систематически разрабатывать художники, архитекторы и скульпторы лишь в эпоху Возрождения: Леонардо да Винчи, Рафаэль, Микеланджело, Тициан и др.

Растущие запросы архитектуры, техники, промышленности, военного дела и живописи привели к формированию специальной математической ветви – начертательной геометрии, которую завершил французский математик Gaspare Monge.

Многогранники

Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранником .

Знаменитый Платон внес огромный вклад в развитие геометрии. Именно он создал пять основных видов многогранников.

Октаэдр

Гексаэдр

Тетраэдр

Икосаэдр

Додекаэдр

Тетраэдр

Тетраэдр составлен из четырех равно-

сторонних треугольников. Каждая его

вершина является вершиной трех тре-

угольников. Сумма плоских углов при

каждой вершине равна 180 градусов.

Тетраэдр имеет 4 грани, 4 вершины и

6 ребер.

Площадь полной поверхности

Объем тетраэдра

Гексаэдр ( куб)

Куб составлен из шести квадратов

Каждая вершина куба является

вершиной трех квадратов.Сумма

плоских углов при каждой

вершине равна 270 градусов.

Куб имеет 6 граней, 8 вершин и

12 ребер .

Площадь полной поверхности

Объем куба

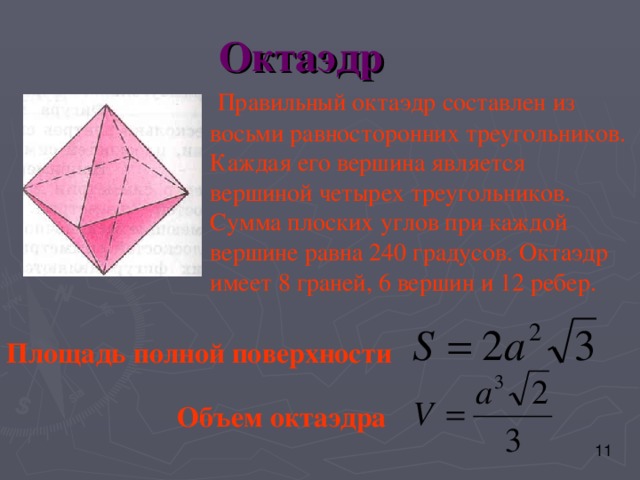
Октаэдр

Правильный октаэдр составлен из

восьми равносторонних треугольников.

Каждая его вершина является

вершиной четырех треугольников.

Сумма плоских углов при каждой

вершине равна 240 градусов. Октаэдр

имеет 8 граней, 6 вершин и 12 ребер.

Площадь полной поверхности

Объем октаэдра

Икосаэдр

Правильный икосаэдр составлен из

двадцати равносторонних

треугольников.Каждая вершина

икосаэдра является вершиной пяти

треугольников.Сумма плоских углов

при каждой вершине равна 300 0 .

Икосаэдр имеет 20 граней,12 вершин

и 30 ребер.

Площадь полной поверхности



3

)

5

3

(

a

5

Объем икосаэдра



V

12

Додекаэдр

Правильный додекаэдр состоит из 12

правильных пятиугольников. Каждая

вершина додекаэдра является

вершиной трех правильных

пятиугольников.Сумма плоских углов

при каждой вершине равна 324 0 .

Додекаэдр имеет 12 граней, 20

вершин и 30 ребер.

Площадь полной поверхности

Объем додекаэдра

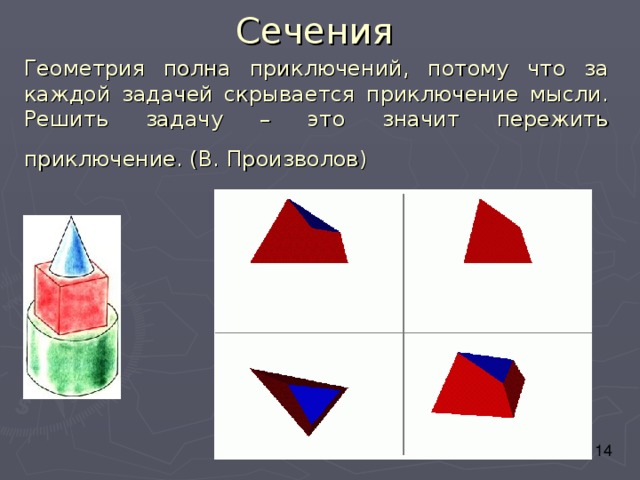
Сечения

Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение. (В. Произволов)

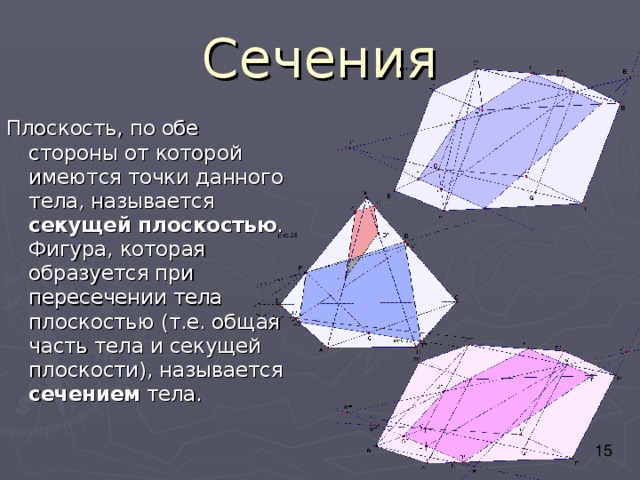
Сечения

Плоскость, по обе стороны от которой имеются точки данного тела, называется секущей плоскостью . Фигура, которая образуется при пересечении тела плоскостью (т.е. общая часть тела и секущей плоскости), называется сечением тела.

Рассмотрим некоторые виды сечений объемных тел

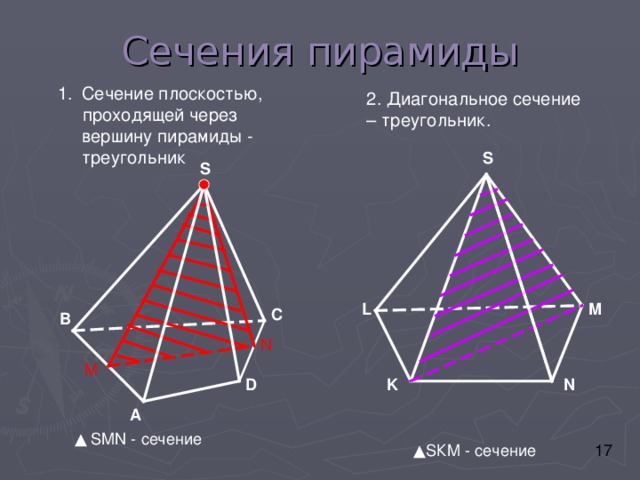
Сечения пирамиды

• Сечение плоскостью,

проходящей через вершину пирамиды - треугольник

2. Диагональное сечение – треугольник.

S

S

M

L

С

В

N

M

N

K

D

А

▲ SMN - сечение

▲ S К M - сечение

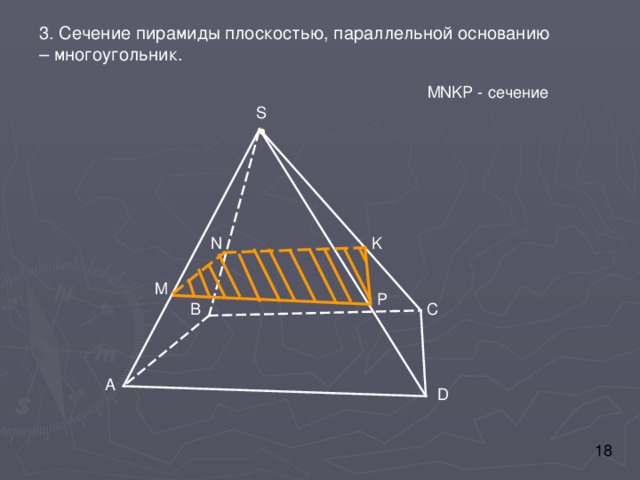
3. Сечение пирамиды плоскостью, параллельной основанию – многоугольник.

MNKP - сечение

S

N

K

M

P

B

C

A

D

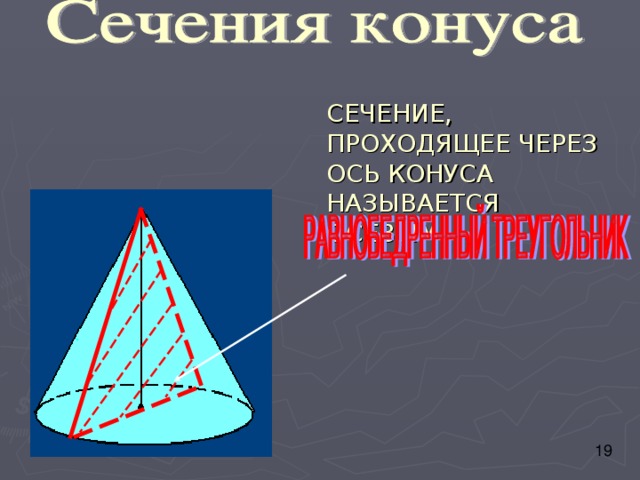
СЕЧЕНИЕ, ПРОХОДЯЩЕЕ ЧЕРЕЗ ОСЬ КОНУСА НАЗЫВАЕТСЯ ОСЕВЫМ

Сечения конуса

Сечение конуса плоскостью,

параллельной основанию

Сечения конуса

Сечение конуса плоскостью,

не параллельной основанию

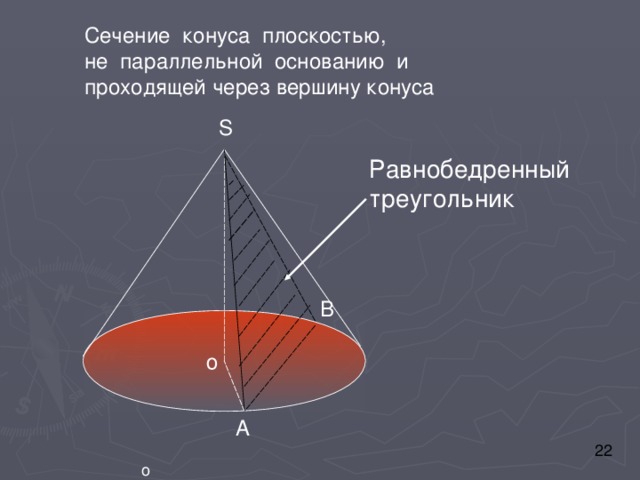
Сечение конуса плоскостью,

не параллельной основанию и проходящей через вершину конуса

S

Равнобедренный треугольник

В

о

А

о

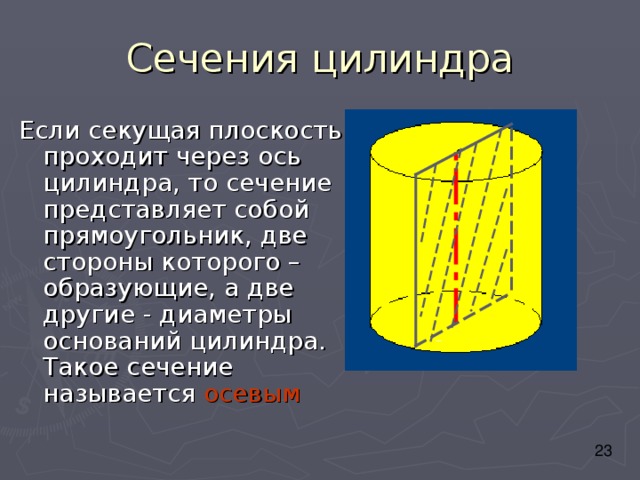
Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого –образующие, а две другие - диаметры оснований цилиндра. Такое сечение называется осевым

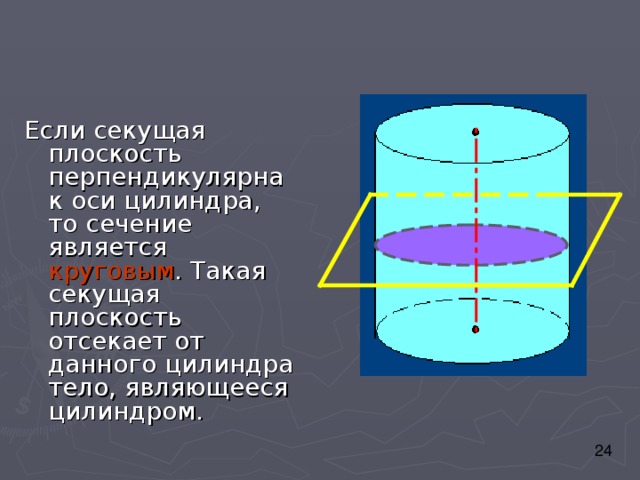
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является круговым . Такая секущая плоскость отсекает от данного цилиндра тело, являющееся цилиндром.

Если секущая плоскость не параллельна ни основанию, ни образующим, то в сечении получается эллипс

Основные методы построения сечений многогранников

1) Аксиоматический метод:

а) Метод следов

б) Метод внутреннего проектирования

2) Комбинированный метод

Существует два основных метода построения сечений многогранников

Для построения сечений аксиоматическим методом необходимо помнить основные аксиомы стереометрии и следствия из них.

Аксиомы стереометрии

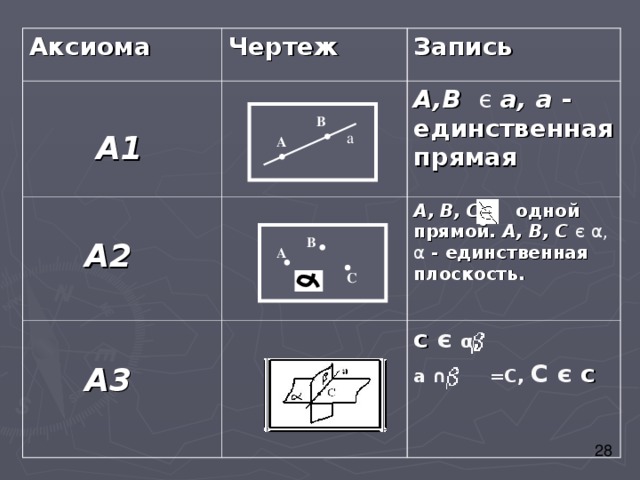
Аксиома

Чертеж

А1

Запись

А2

А,В є а, а - единственная прямая

А3

А, В, С одной прямой. А, В, С є α , α - единственная плоскость.

с є α ,

а ∩ =С, С є с

В

а

А

В

А

С

Следствия из аксиом стереометрии

Чертеж.

Сл.1

Формулировка.

Сл.2

Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.

Сл.3.

Через две пересекающиеся прямые можно провести плоскость и притом только одну.

Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну.

Правило для самоконтроля.

• Если многогранник выпуклый, то сечение выпуклый многоугольник.
• Вершины многоугольника всегда лежат на ребрах многогранника.
• Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении.
• Если точки сечения лежат на гранях многогранника, то они лежат на сторонах многоугольника, который получится в сечении.
• Две стороны многоугольника, который получится в сечении, не могут принадлежать одной грани многогранника.
• Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.

Способ следов

Способ следов заключается в следующем. Вначале строят на основной плоскости след секущей плоскости (причем за основную плоскость принимают большей частью плоскость основания геометрического тела).Затем, используя след секущей плоскости, находят точки встречи ребер многогранника с секущей плоскостью. Используя полученные ( и данные ) точки, получают следы секущей плоскости на гранях многогранника.

Пример 1

Дано: трехгранная призма АВСА 1 В 1 С 1 . D Є A 1 C 1 ,E Є CC 1 ,F Є BB 1 Построить сечение призмы плоскостью, проходящей через три заданные точки

B

A

C

F

E

A1

B1

D

C1

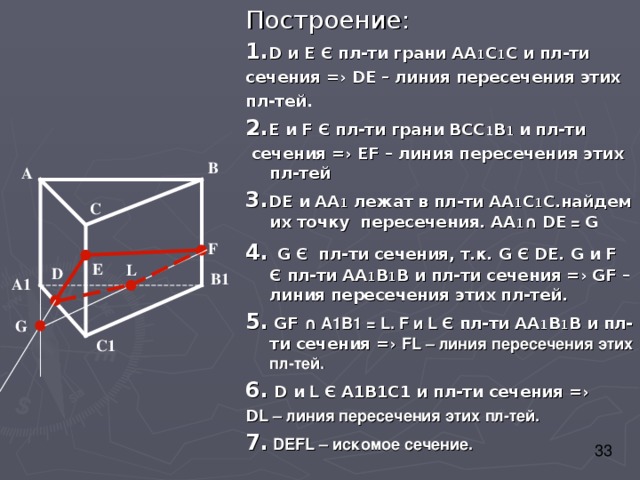
Построение:

1. D и E Є пл-ти грани АА 1 С 1 С и пл-ти

сечения =› D Е – линия пересечения этих

пл-тей.

2. Е и F Є пл-ти грани ВСС 1 В 1 и пл-ти

сечения =› Е F – линия пересечения этих пл-тей

3. DE и AA 1 лежат в пл-ти АА 1 С 1 С.найдем их точку пересечения. АА 1 ∩ DE = G

4. G Є пл-ти сечения, т.к. G Є DE . G и F Є пл-ти АА 1 В 1 В и пл-ти сечения =› GF – линия пересечения этих пл-тей.

5. GF ∩ А1В1 = L. F и L Є пл-ти АА 1 В 1 В и пл-ти сечения =› FL – линия пересечения этих пл-тей.

6. D и L Є А1В1С1 и пл-ти сечения =›

D L – линия пересечения этих пл-тей.

7. DEFL – искомое сечение.

B

A

C

F

E

L

D

B1

A1

G

C1

Алгоритм построения сечения методом следов

• 1.Выяснить имеются ли в одной грани 2 точки сечения (если да, то через них можно провести сторону сечения).
• 2.Построить след сечения на плоскости основания многогранника.
• 3.Найти дополнительную точку сечения на ребре многогранника ( продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом).
• 4.Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения ее с ребрами грани.
• 5.Выполнить п.1

Метод внутреннего проектирования

Метод внутреннего проектирования является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.

Пример 2

Дано:

РАВС DE - пирамида. R Є PE, M Є PA,

F Є PC.

Построить сечение пирамиды плоскостью, проходящей через точки R , M , F .

P

.

R

.

M

.

D

E

F

A

C

B

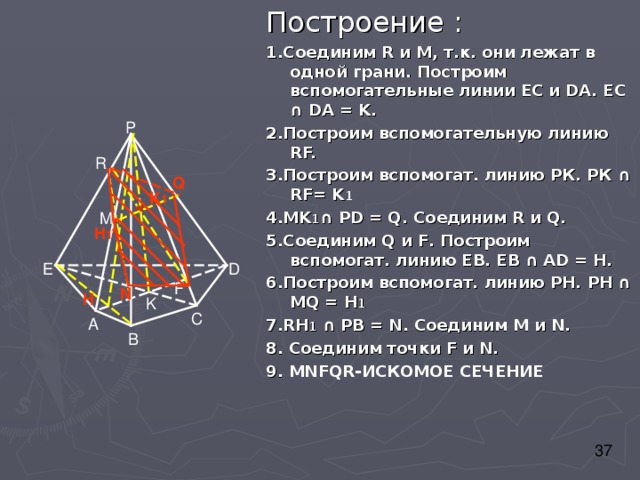
Построение :

1.Соединим R и M , т.к. они лежат в одной грани. Построим вспомогательные линии ЕС и DA . ЕС ∩ DA = K.

2. Построим вспомогательную линию RF.

3. Построим вспомогат. линию РК. РК ∩ RF= K 1

4.MK 1 ∩ PD = Q. Соединим R и Q .

5.Соединим Q и F . Построим вспомогат. линию ЕВ. ЕВ ∩ А D = H .

6.Построим вспомогат. линию РН. РН ∩ М Q = H 1

7.RH 1 ∩ PB = N. Соединим М и N .

8. Соединим точки F и N .

9. MNFQR- ИСКОМОЕ СЕЧЕНИЕ

P

.

R

.

Q

.

K 1

M

H 1

.

E

D

F

N

H

K

C

A

B

Алгоритм построения сечения методом внутреннего проектирования

Комбинированный метод

Сущность этого метода состоит в том, что на некоторых этапах построения сечения применяется или метод следов, или метод внутреннего проектирования, а на других этапах построение этого сечения осуществляется с использованием теорем о параллельности в пространстве и др.

Практическое применение

Геометрические сечения широко применяются в строительстве, архитектуре, мостостроении, технике, а также в техническом черчении для выявления формы и внутреннего устройства предметов.

ТЕСТ

1.Какой из многоугольников не может получиться в сечении куба плоскостью?

• а) пятиугольник
• б) семиугольник
• в) шестиугольник
• г) трапеция

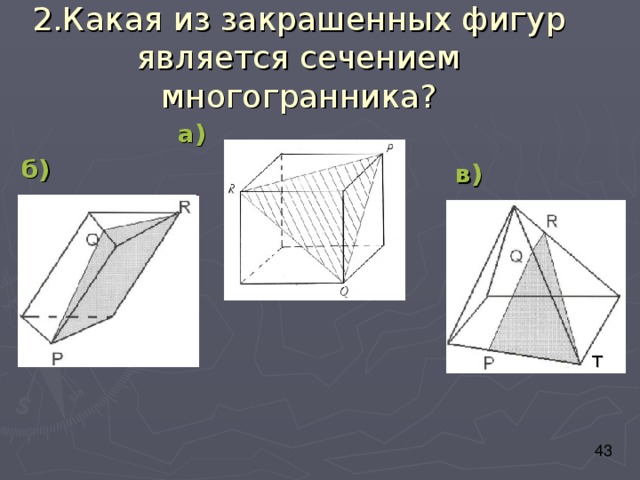
2.Какая из закрашенных фигур является сечением многогранника?

а)

б)

в)

Т

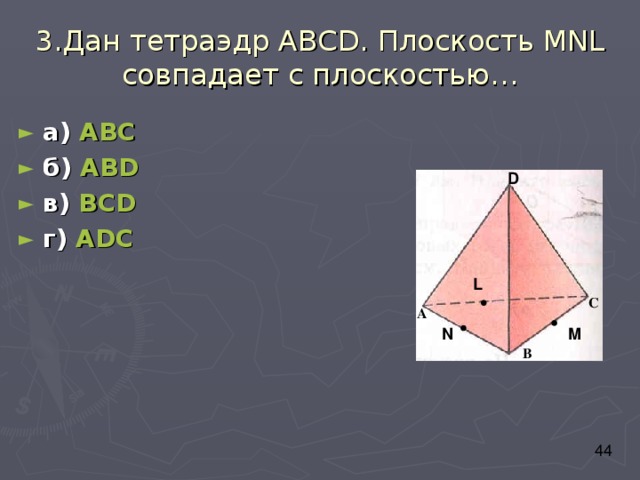
3.Дан тетраэдр АВС D . Плоскость М NL совпадает с плоскостью…

• а) АВС
• б) АВ D
• в) ВС D
• г) А D С

D

L

С

А

M

N

В

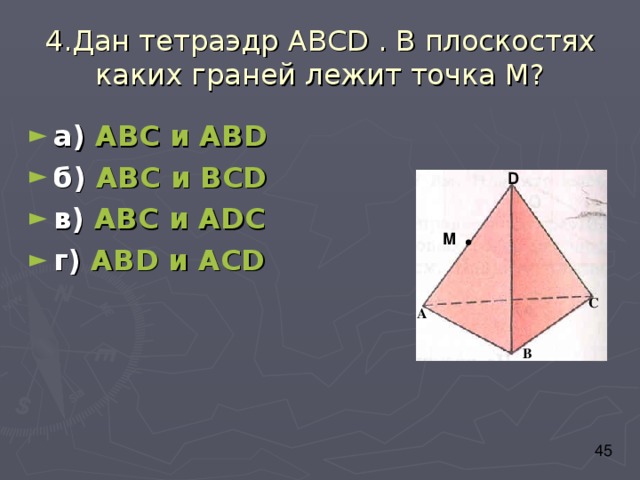
4.Дан тетраэдр АВС D . В плоскостях каких граней лежит точка М?

• а) АВС и АВ D
• б) АВС и ВС D
• в) АВС и А D С
• г) АВ D и АС D

D

M

С

А

В

5.Дан тетраэдр АВС D . Точка М лежит на ребре А D ,точка N на ребре В D ,точка L - на D С. Какие точки не лежат в одной грани?

• а) М и N
• б) М и L
• в) N и L
• г) нет таких точек

D

L

M

N

С

А

В

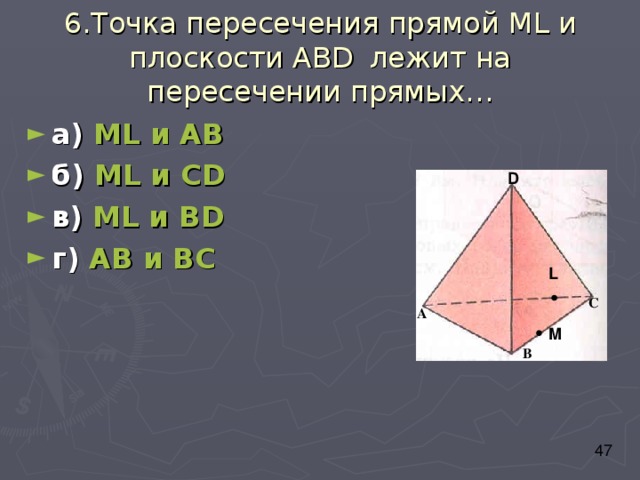
6.Точка пересечения прямой М L и плоскости АВ D лежит на пересечении прямых…

• а) М L и АВ
• б) М L и С D
• в) М L и В D
• г) АВ и ВС

D

L

С

А

M

В

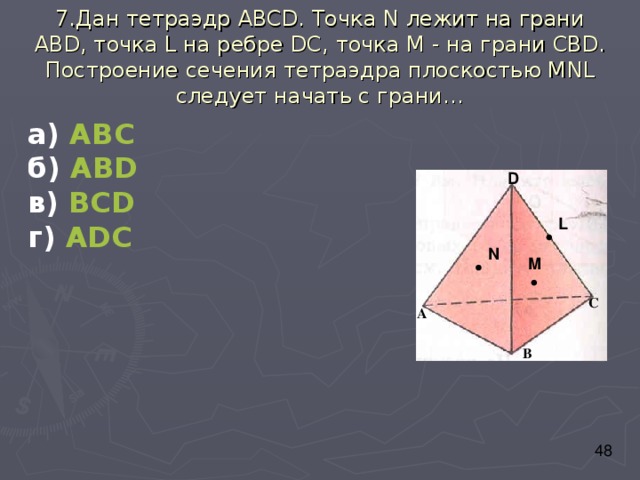
7.Дан тетраэдр ABCD. Точка N лежит на грани АВ D , точка L на ребре DC , точка М - на грани СВ D. Построение сечения тетраэдра плоскостью М NL следует начать с грани…

а) АВС

б) АВ D

в) ВС D

г) А DC

D

L

N

M

С

А

В

8.Дан тетраэдр АВС . Точка М лежит на ребре А D , точка N в плоскости АВ D . Как расположены прямая М N и плоскость В D С?

• а) М N лежит в плоскости В D С
• б) М N пересекает плоскость В D С
• в) М N параллельна плоскости В D С
• г) М N скрещивается с В D С

D

M

N

С

А

В

ЗАДАЧИ

ЗАДАЧА 1

Построение:

1). Соединим т. P и т. Q (т.к. они лежат в одной плоскости FF 1 E 1 E) . Получился отрезок PQ .

2). Соединим т. Q и т. R ( т.к. они лежат в одной плоскости EE 1 D 1 D) . Получился отрезок QR .

3). Соединим т. R и т. P .

Треугольник PQR – искомое сечение данной призмы.

Дано : точки P , Q, R, лежащие на ребрах призмы . Построить сечение, проходящее через данные точки.

B 1

C 1

D 1

A 1

F 1

E 1

Q

C

B

D

А

R

E

F

P

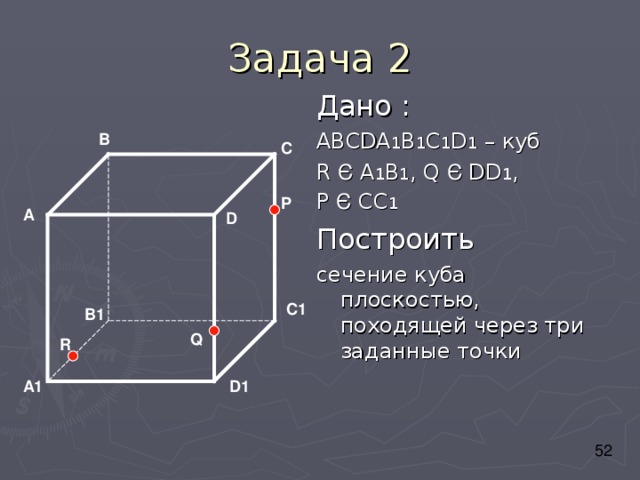
Дано :

АВС DA 1 B 1 C 1 D 1 – куб

R Є A 1 B 1 , Q Є DD 1 ,

P Є CC 1

Построить

сечение куба плоскостью, походящей через три заданные точки

В

С

P

А

D

C1

B1

Q

R

A1

D1

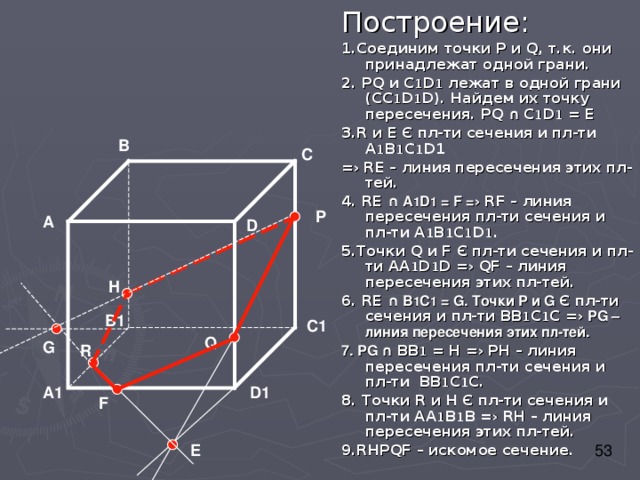
Построение:

1.Соединим точки P и Q , т.к. они принадлежат одной грани.

2. PQ и С 1 D 1 лежат в одной грани (СС 1 D 1 D) . Найдем их точку пересечения. PQ ∩ C 1 D 1 = E

3.R и E Є пл-ти сечения и пл-ти A 1 B 1 C 1 D1

=› RE – линия пересечения этих пл-тей.

4. RE ∩ A 1 D 1 = F = › RF – линия пересечения пл-ти сечения и пл-ти А 1 В 1 С 1 D 1.

5. Точки Q и F Є пл-ти сечения и пл-ти АА 1 D 1 D =› QF – линия пересечения этих пл-тей.

6. RE ∩ В 1 С 1 = G. Точки P и G Є пл-ти сечения и пл-ти ВВ 1 С 1 С =› PG – линия пересечения этих пл-тей.

7. PG ∩ ВВ 1 = Н =› РН – линия пересечения пл-ти сечения и пл-ти ВВ 1 С 1 С.

8. Точки R и Н Є пл-ти сечения и пл-ти АА 1 В 1 В =› R Н – линия пересечения этих пл-тей.

9. RHPQF – искомое сечение.

В

С

P

А

D

H

B1

C1

Q

G

R

D1

A1

F

E

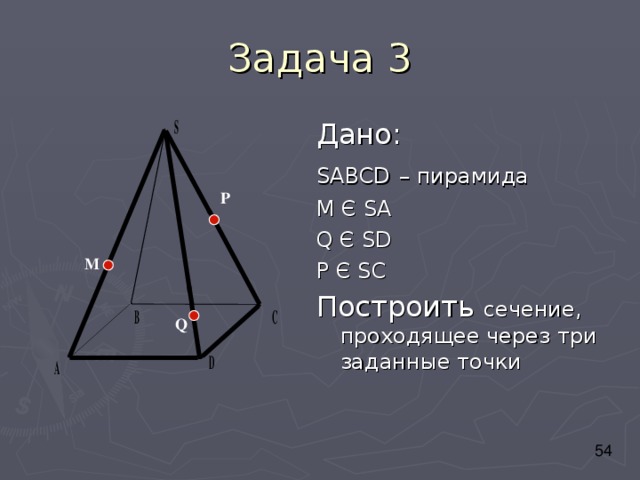
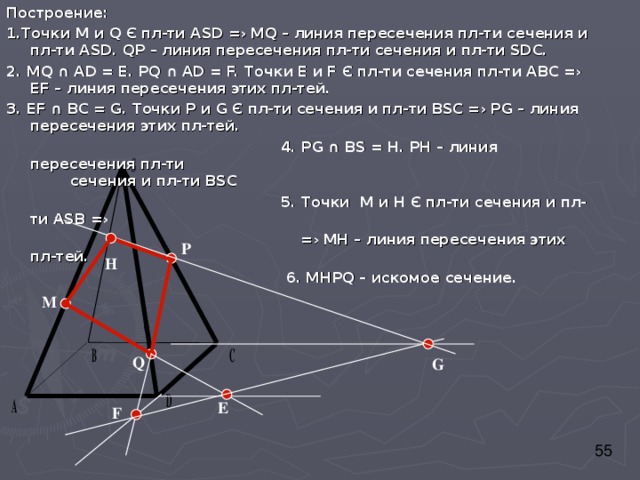
Дано:

SABCD – пирамида

М Є SA

Q Є SD

P Є SC

Построить сечение, проходящее через три заданные точки

P

M

Q

Построение:

1 . Точки M и Q Є пл-ти ASD =› MQ – линия пересечения пл-ти сечения и пл-ти ASD . Q Р – линия пересечения пл-ти сечения и пл-ти SD С.

2. MQ ∩ AD = Е. Р Q ∩ AD = F. Точки Е и F Є пл-ти сечения пл-ти АВС =› Е F – линия пересечения этих пл-тей.

3. Е F ∩ ВС = G. Точки Р и G Є пл-ти сечения и пл-ти В S С =› Р G – линия пересечения этих пл-тей.

4. Р G ∩ В S = Н. РН – линия пересечения пл-ти сечения и пл-ти В S С

5. Точки М и Н Є пл-ти сечения и пл-ти AS В =›

=› МН – линия пересечения этих пл-тей.

6. МНР Q – искомое сечение.

P

H

M

Q

G

Е

F

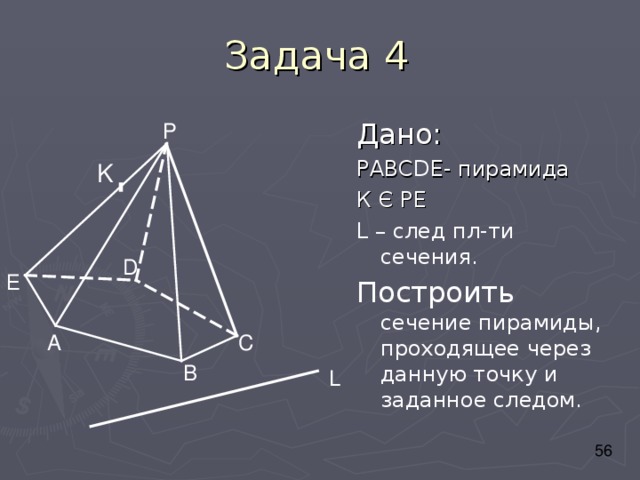
Дано:

РАВС D Е- пирамида

К Є РЕ

L – след пл-ти сечения.

Построить сечение пирамиды, проходящее через данную точку и заданное следом.

Р

K

D

Е

А

С

В

L

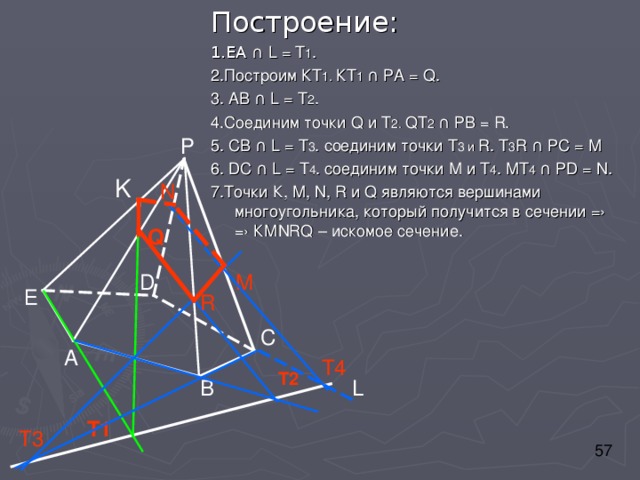
Построение:

1.ЕА ∩ L = T 1 .

2.Построим КТ 1 . КТ 1 ∩ РА = Q .

3. АВ ∩ L = Т 2 .

4.Соединим точки Q и Т 2. Q Т 2 ∩ РВ = R.

5. СВ ∩ L = Т 3 . соединим точки Т 3 и R . Т 3 R ∩ РС = М

6. DC ∩ L = Т 4 . соединим точки М и Т 4 . МТ 4 ∩ Р D = N.

7. Точки К, М, N , R и Q являются вершинами многоугольника, который получится в сечении =› =› КМ NRQ – искомое сечение.

Р

K

N

Q

D

M

Е

R

С

А

T4

T2

L

В

T1

T3

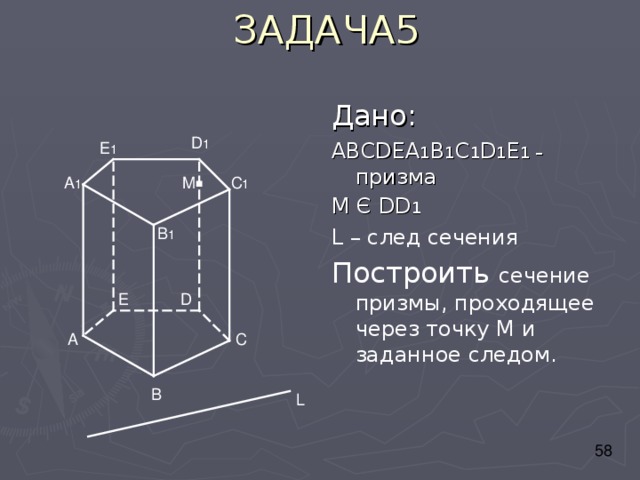
Дано:

АВС DEA 1 B 1 C 1 D 1 E 1 – призма

М Є DD 1

L – след сечения

Построить сечение призмы, проходящее через точку М и заданное следом.

D 1

E 1

.

A 1

C 1

M

B 1

D

E

A

C

B

L

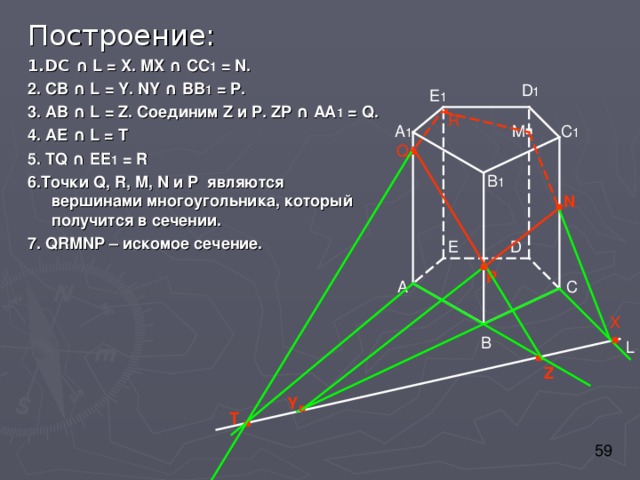
Построение:

1.DC ∩ L = X. MX ∩ CC 1 = N.

2. CB ∩ L = Y. NY ∩ BB 1 = P.

3. AB ∩ L = Z. Соединим Z и P . ZP ∩ АА 1 = Q.

4. АЕ ∩ L = Т

5 . TQ ∩ EE 1 = R

6 . Точки Q, R, M, N и P являются вершинами многоугольника, который получится в сечении.

7. QRMNP – искомое сечение.

D 1

E 1

.

.

R

.

C 1

A 1

M

Q

B 1

.

N

.

D

E

P

C

A

.

X

.

B

L

Z

.

.

Y

T

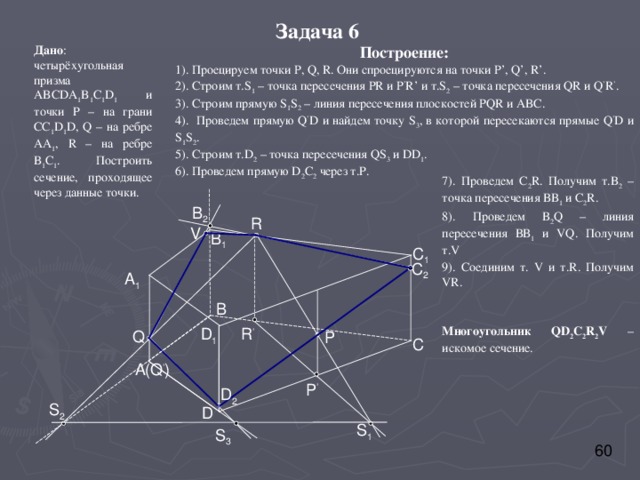
Задача 6

Построение:

1). Проецируем точки P, Q, R . Они спроецируются на точки P’, Q’, R’.

2). Строим т. S 1 – точка пересечения PR и P ’ R’ и т. S 2 – точка пересечения QR и Q ’ R ’ .

3) . Строим прямую S 1 S 2 – линия пересечения плоскостей PQR и ABC .

4). Проведем прямую Q ’ D и найдем точку S 3 , в которой пересекаются прямые Q ’ D и S 1 S 2 .

5). Строим т. D 2 – точка пересечения QS 3 и DD 1 .

6). Проведем прямую D 2 C 2 через т.Р.

Дано : четырёхугольная призма ABCDA 1 B 1 C 1 D 1 и точки Р – на грани CC 1 D 1 D , Q – на ребре АА 1 , R – на ребре В 1 С 1 . Построить сечение, проходящее через данные точки.

7). Проведем С 2 R . Получим т.В 2 – точка пересечения ВВ 1 и С 2 R .

8). Проведем В 2 Q – линия пересечения ВВ 1 и VQ . Получим т. V

9). Соединим т. V и т. R . Получим VR .

Многоугольник QD 2 C 2 R 2 V – искомое сечение.

B 2

R

V

B 1

C 1

C 2

A 1

B

D 1

R ’

Q

P

C

A

(Q ’ )

P ’

D 2

S 2

D

S 1

S 3

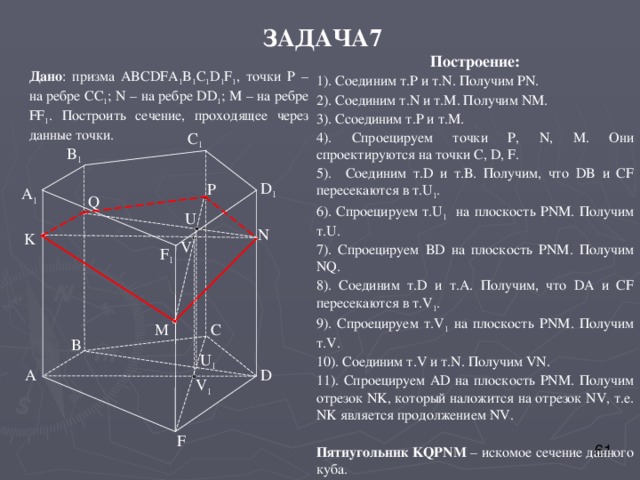
ЗАДАЧА7

Построение:

1). Соединим т. P и т. N . Получим PN .

2). Соединим т. N и т. M . Получим NM .

3). C соединим т. P и т.М.

4). Спроецируем точки Р, N, M. Они спроектируются на точки С, D, F .

5). Соединим т. D и т.В. Получим, что DB и CF пересекаются в т. U 1 .

6). Спроецируем т. U 1 на плоскость PNM . Получим т. U .

7). Спроецируем BD на плоскость PNM . Получим NQ .

8). Соединим т. D и т. A . Получим, что DA и CF пересекаются в т. V 1 .

9). Спроецируем т. V 1 на плоскость PNM . Получим т. V .

10). Соединим т. V и т. N . Получим VN .

11). Спроецируем AD на плоскость PNM . Получим отрезок NK , который наложится на отрезок NV , т.е. NK является продолжением NV .

Пятиугольник KQPNM – искомое сечение данного куба.

Дано : призма ABCDFA 1 B 1 C 1 D 1 F 1 , точки Р – на ребре СС 1 ; N – на ребре DD 1 ; М – на ребре FF 1 . Построить сечение, проходящее через данные точки.

C 1

B 1

D 1

P

A 1

Q

U

N

K

V

F 1

M

C

B

U 1

D

A

V 1

F

ЗАДАЧА8

Построение:

1). Спроецируем т.Р и т. N на плоскость ABCD . Получим точки P 1 , N 1 .

2). Соединим т. Р и т. N . Получим PN .

3). Соединим т. P 1 и т. N 1 . Получим P 1 N 1 .

4). Продолжим PN и P 1 N 1 . Получим, что они пересекаются в т. X . 5).Соединим т.Х и т.М. Получим, что AD и XM пересекаются в т. Q, а ХМ пересекает CD в т. R .

6). Продолжим ВС и ХМ. Получим, что они пересекаются в т.У.

Дано : параллелепипед ABCDA 1 B 1 C 1 D 1 и точки : М – на грани ABCD , N – на грани AA 1 B 1 B, Р – на грани ВВ 1 С 1 С. Построить сечение, проходящее через данные точки.

Z

T

7). Соединим т.Р и т.У. Получим, что РУ пересекает ВС в т. S и в т.Т.

8). Продолжим ВВ 1 и РУ. Получим, что они пересекаются в т. Z .

9). Соединим т. Z и т.Х. Получим, что XZ пересекается с А 1 B 1 в т. U ; XZ пересекается с AA 1 в т. F .

Шестиугольник FUTSRQ – искомое сечение данного параллелограмма

B 1

C 1

U

P

A 1

D 1

F

S

N

Y

P 1

C

B

N 1

R

M

D

A

Q

X

Заключение

В ходе проведенной исследовательской работы были рассмотрены основные виды многогранников и сечений, различные методы построения сечений многогранников, выявлены наиболее рациональные методы построения сечений.

Данная работа расширила мои представления о методах построения сечений многогранников, систематизировала знания и умения, способствовала развитию пространственного представления.

Список используемой литературы

• Атанасян Л. С.: “Геометрия 10 – 11 класс”. Москва «Просвещение» 2003.
• Литвиненко В. Н.: “Задачи на развитие пространственных представлений”. Москва «Просвещение» 1991.
• В.В.Прасолов, И.Ф.Шарыгин "Задачи по стереометрии", МОСКВА "Наука", 1989г
• Л.Е.Силаев "Универсальность метода сечений в стереометрии" 1990 - 1997 гг.
• Большая советская энциклопедия .
• Материалы с сайта http//www.math.ru

Верный ответ!

Неверный ответ!