Презентация к урокам повторения "Решение текстовых задач при подготовке к ОГЭ"

Кусей Л.А.

учитель математики

МБОУ «СОШ №1 им. Героя Советского Союза П.В. Масленникова ст. Архонская»

2016 г.

«Умение решать задачи – практически искусство, подобно плаванию, или катанию на коньках, или игре на фортепиано: научиться этому можно, лишь подражая избранным образцам и постоянно тренируясь»

Д. Пойа

• Одним из важных вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач. В процессе обучения математике задачи выполняют разнообразные функции. Задачи являются эффективным и незаменимым средством усвоения учащимися понятий и методов школьного курса математики.
• Правильная методика обучения решению математических задач играет существенную роль в формировании высокого уровня математических знаний, умений и навыков учащихся. С задачи учащиеся знакомятся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, для решения вопросов, которые возникают в жизни человека.

• Этапы решения задач являются формами развития мыслительной деятельности учащихся. Наблюдается активизация их мыслительной работы, формируется умение проводить исследование. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, абстрактное мышление, умение применять теорию к решению конкретных задач и закрепление на практике приобретённых умений и навыков.
• Текстовые задачи входят в ОГЭ и ЕГЭ, поэтому, данная тема имеет важнейшее значение в обучении математике.

Для текстовых задач не существует единого алгоритма решения – в этом вся их сложность. Тем не менее существуют типовые задачи, которые вполне решаются стандартно.

В обучении составлению уравнений оказывается весьма полезным такие упражнения:

Записать в виде математического выражения:

• х на 5 больше у; х в 5 раз больше у; z на 8 меньше, чем х; частное от деления а на в в 1,5 раза больше в; п меньше х в 3,5 раза; квадрат суммы х и у равен 7; х составляет 60% от у; м больше п на 15%.
• х на 5 больше у;
• х в 5 раз больше у;
• z на 8 меньше, чем х;
• частное от деления а на в в 1,5 раза больше в;
• п меньше х в 3,5 раза;
• квадрат суммы х и у равен 7;
• х составляет 60% от у;
• м больше п на 15%.

Классификация текстовых задач

• Задачи на движение.
• Задачи на работу.
• Задачи на смеси и сплавы.
• Задачи на проценты.
• Задачи на прогрессии.

Подходы к решению текстовых задач

Наиболее распространенный, довольно эффективный способ использования таблиц. В зависимости от типа решаемой задачи столбики в таблице будут иметь разные названия.

Задачи на движение

Все задачи решаются по формуле S =Vt .

В качестве переменной x удобно выбрать скорость,

тогда задача точно решится.

Уравнения составляются по одновременным событиям.

Замечания:

• если время события задано, то удобнее составлять уравнение на путь;
• если уравнений меньше, чем неизвестных, то нужно ввести в систему искомую величину.

Задача

Из А в В выехали одновременно два автомобиля. Первый проехал весь путь с постоянной скоростью. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 14 км/ч, а вторую половину пути – со скоростью 105 км/ч. Прибыли в В одновременно. Скорость первого - ? Если известно, что она больше 50 км/ч. Ответ в км/ч.

Решение

Задачи на работу

А = рt, из этой формулы легко найти р (производительность) или t.

Если объем работы не важен и нет никаких данных, позволяющих его найти – работу принимаем за единицу.

Если трудятся два рабочих (два экскаватора и т.д.) – их производительности складываются.

В качестве переменной удобно взять производительность.

Задача

Заказ на деталей первый рабочий выполняет на час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на деталь больше?

Решение

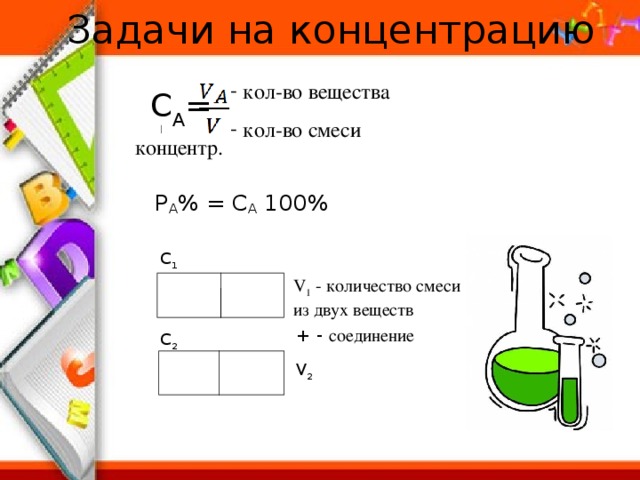
Задачи на концентрацию

• кол-во вещества
• кол-во смеси

С A =

|

концентр.

P A % = C A 100%

С 1

V 1 - количество смеси из двух веществ

+ - соединение

С 2

V 2

}

C 1

C 1 V 1

V 1

C

CV

C 2

V

C 2 V 2

V 2

C 1 V 1 + C 2 V 2 = CV – основное уравнение

V 1 + V 2 = V – дополнительное уравнение

Задача

При смешивании 10% раствора с 5% раствором получено 5 кг 6% раствора. Сколько каждого раствора было взято?

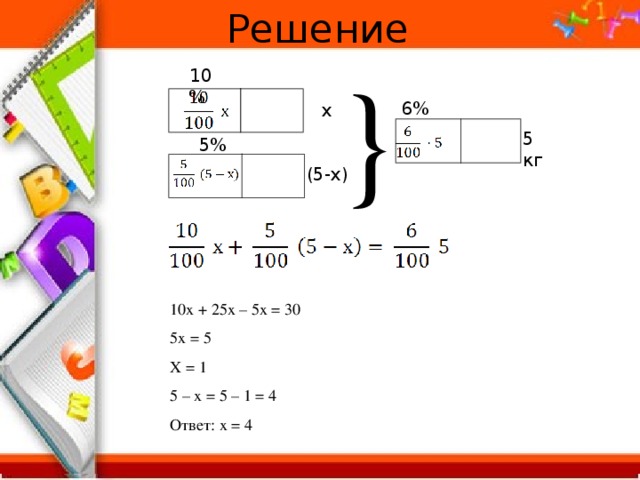
Решение

}

10%

6%

x

5 кг

5%

(5-х)

10х + 25х – 5х = 30

5х = 5

Х = 1

5 – х = 5 – 1 = 4

Ответ: х = 4

Задача

• Имеется два сплава. Первый сплав содержит никеля 10%, второй 30% — никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий никеля 25%. На сколько килограммов масса первого сплава меньше массы второго?

Решение

• Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой х+у=200.

10% от х

30% от у

25% от 200

+

=

х+у = 200

0,1х + 0,3у = 0.25*200

Ответ: 100

Задачи на проценты

Если величина а изменяется на х%, то ее новое значение

х%

y%

z%

Задача

В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

Решение

Задачи на прогрессии

Арифметическая прогрессия:

Геометрическая прогрессия:

Бесконечно убывающая:

Задача

Сумма первых трех членов возрастающей геометрической прогрессии равна 13, а их произведение 27. Вычислите сумму первых пяти членов этой прогрессии.

Решение