Презентация к уроку "Медианы, биссектрисы и высоты треугольника"

МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА

Составитель:

учитель математики

Фоминок С.С.

Перпендикуляр к прямой

А  а, АН  а

Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а , если прямые АН и а перпендикулярны.

А

н

а

Теорема о перпендикуляре

Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

А

н

а

Медиана треугольника

В

АМ = МС

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника .

С

А

М

ВМ – медиана треугольника

Медиана треугольника

- Нам вершина не нужна,

Медиана учит сына.

– Наше дело сторона,

А точнее – середина.

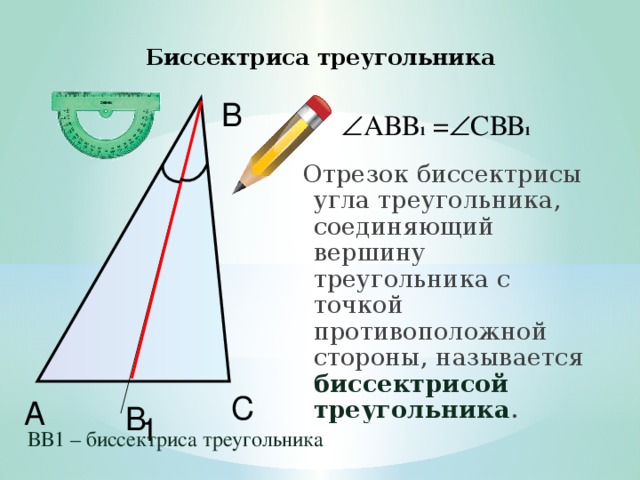
Биссектриса треугольника

В

 АВВ 1 =  СВВ 1

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника .

С

А

В

1

ВВ1 – биссектриса треугольника

Биссектриса треугольника

Высота треугольника

В

ВН  АС

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника .

С

Н

А

ВН – высота треугольника

Высота треугольника

Высота похожа на кота, Который, выгнув спину, И под прямым углом Соединит вершину И сторону хвостом.

Медианы в треугольнике

В любом треугольнике медианы пересекаются в одной точке.

о

Точку пересечения медиан (в физике) принято называть центром тяжести .

Биссектрисы в треугольнике

В любом треугольнике биссектрисы пересекаются в одной точке.

о

Точка пересечения биссектрис треугольника есть центр вписанной в треугольник окружности .

Высоты в треугольнике

Высоты в треугольнике

В любом треугольнике высоты или их продолжения пересекаются в одной точке.

о

Точку пересечения высот называют ортоцентром .

Задание

По рисунку определите

а) медиану;

б) биссектрису;

в) высоту

треугольника MKT.

а) Медиана – отрезок

б) Биссектриса – отрезок

в) Высота – отрезок

ТВ

КА

МС

Выберите правильный ответ:

1.

В

Дано: ∆ АВС,АО=ОК,

АВ=6,3см,

ВС=6,5см,

АС=6,7см

Найти: СК.

К

О

С

А

Варианты ответов:

а) 6,4см б) 6,7см

в) 6,5см г) 6,3см

Выберите правильный ответ:

2.

E

Дано: ∆ МОК и ∆ ЕОF,

ОН=ОN,

ЕN=7,8cм,

ОЕ=8,6см,

НМ=6,3см.

Найти: МК

N

М

О

F

Н

К

Варианты ответов:

а) 13,9см б) 14,1см

в) 14,9см г) 16,4см

Выберите правильный ответ:

3.

В треугольниках АВС и КРМ проведены биссектрисы ВО и РЕ,

причём ∆АВО=∆КРЕ.

Найдите отрезок ЕМ, если АС=9см, а ЕМ больше КЕ на 3,8см.

Варианты ответов:

а) 6,4см б) 5,4см

в) 2,6см г) 4,8см

Ответы:

1) г

2)б

3)а

Домашнее задание

I уровень : п. 16,17, знать основные определения и формулировки утверждений и теорем.

II уровень : п. 16,17, знать основные определения и формулировки утверждений, и доказательство теорем.

На альбомных листах (А4) в каждом из треугольников (остроугольном, прямоугольном и тупоугольном) провести медианы, биссектрисы и высоты.

Спасибо за урок!

Источники:

1.Атанасян Л.С., Бутузов В.Ф. и др. Геометрия 7 – 9. М., «Просвещение», 2011 г.

2.Елизарова С. Ребятам о зверятах. // Народное образование. № 9 – 10, 1993 г.

3.Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. Рабочая тетрадь для 7 класса. – М., «Просвещение», 2009 г. – № 63.

4.Картинка на стр. №1: http://rpp.nashaucheba.ru/pars_docs/refs/11/10044/

5.Карандаш: http:// ai-cdr.ucoz.ru/kartinki/karandash.gif .

6.Транспортир: http:// офиснаяслужба.рф/images/72142b.jpg .

7.Линейка: http:// img.office-planet.ru/goods/210051/4e85b7681bf74_x.png .