Презентация к уроку "Определение производной" 10 класс

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №10 г. Ногинска Московской области

Определение производной

Автор Лукахина Марина Юрьевна

Ногинск 2013 г.

§27. Определение производной.

Устные упражнения

Найдите тангенс угла наклона прямой к положительному направлению оси абсцисс и угловой коэффициент этой прямой

у

5

Ответ : tgα = 0,6; k = 0,6.

α

2

α

х

6

1

О

Устные упражнения

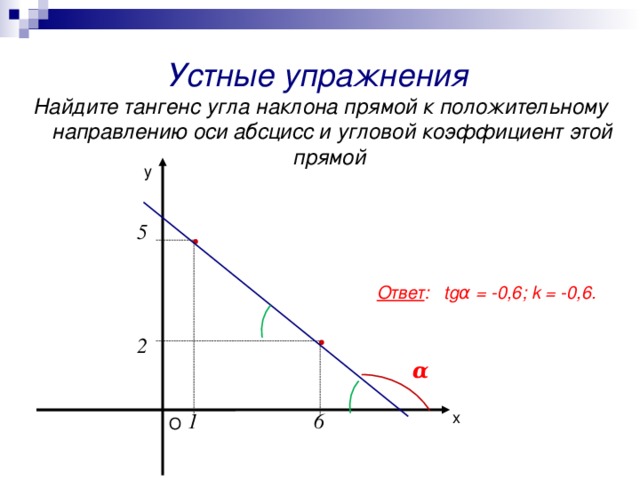
Найдите тангенс угла наклона прямой к положительному направлению оси абсцисс и угловой коэффициент этой прямой

у

5

Ответ : tgα = -0,6; k = -0,6.

2

α

х

1

6

О

Определение 2 (§26)

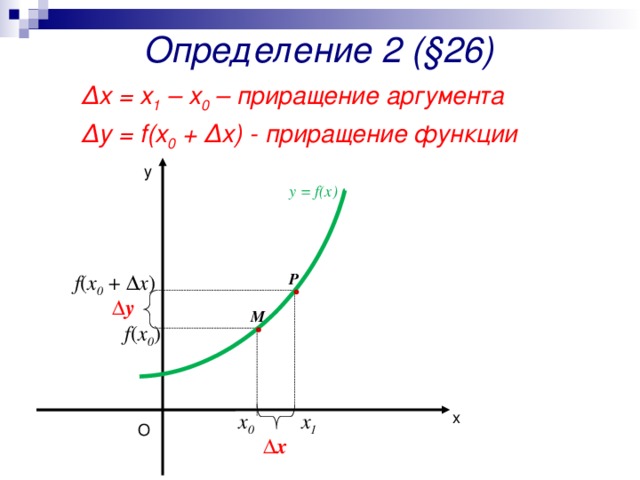
∆ х = х 1 – х 0 – приращение аргумента

∆ y = f(x 0 + ∆х) - приращение функции

у

у = f(x)

f ( х 0 + ∆x )

P

∆ y

M

f ( х 0 )

х 1

х

х 0

О

∆ x

1. Задачи, приводящие к понятию производной.

Задача 1 ( о скорости движения)

s = s(t)

∆ s

х

М

P

OM = s(t)

О

OP = s(t + ∆t)

MP = OP – OM = s(t + ∆t) – s(t) = ∆s

касательная

секущая

Определения секущей и касательной к графику функции

у

у = f(x)

P

M

О

х

Задача 2 (о касательной к графику функции).

k сек. = tg β

у

у = f(x)

f ( a + ∆x )

P

∆ y

β

M

f ( a )

α

β

k кас. = tg α

a

х

a+ ∆x

О

∆ x

2. Определение производной.

Определение.

у

у = f(x)

P

f ( х 0 + ∆x )

∆ y

M

f ( х 0 )

х

х 0

х 1

О

∆ x

Физический смысл производной

s = s(t)

х

М

О

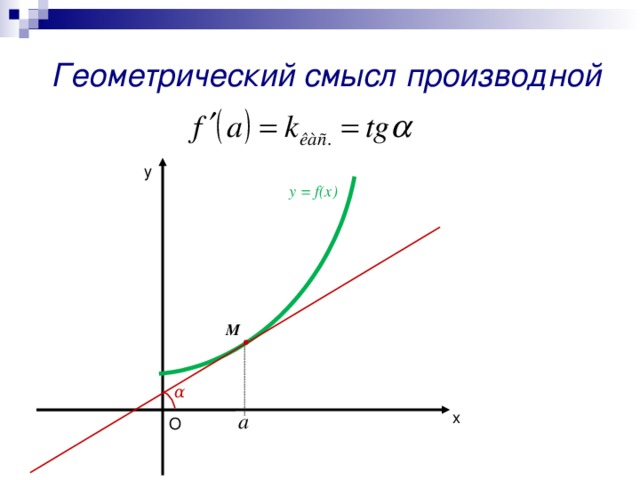
Геометрический смысл производной

у

у = f(x)

M

α

а

х

О

Алгоритм нахождения производной функции у = f(x)

• Зафиксировать значение х, найти f(x).
• Дать аргументу приращение Δх, перейти в новую точку х + Δх, найти f(x + Δх).
• Найти приращение функции Δу = f(x + Δх) - f(x).
• Составить отношение
• Вычислить

Этот предел и есть f’(x).

3. Примеры применения геометрического смысла производной.

Ответ : 4.

Ответ : 1

Ответ : -1

Формулы дифференцирования