Презентация к уроку "Звездный час"

Муниципальное казенное общеобразовательное учреждение

Сортавальского муниципального района Республики Карелия

Кааламская средняя общеобразовательная школа

• Звездный час

Обобщающий урок по геометрии

для учащихся 8 класса

Кааламо 2016 г .

1 тур

«Отгадай фигуру»

7)

М

5)

1)

а

О

2)

В

А

1

2

О

3)

6 )

В

4)

С

А

1

2

В

А

С

1. Об этой геометрической фигуре говорят, что она делит плоскость на две полуплоскости.

2. Об этой геометрической фигуре говорят, что у нее есть «дополнительный родственник».

3. Эта геометрическая фигура имеет длину.

4. Эта геометрическая фигура не имеет размера, но все в геометрии связано с ней .

«Углы.Прямые»

2 тур

с

• Выберите верные утверждения:

а) ∠ 1 и ∠ 3 – вертикальные;

с) ∠ 5 и ∠ 1 – односторонние;

в) ∠ 7 и ∠ 6 – соответственные;

г) ∠ 5 и ∠ 3 – накрест лежащие;

д) ∠ 2 и ∠ 4 – смежные;

е) ∠ 7 и ∠ 1 – накрест лежащие;

ж) ∠ 3 и ∠ 7 – односторонние.

а

1

6

3

8

5

7

в

2

4

2. Выберите верные утверждения:

Прямые а и в параллельны, если…

а) ∠ 1 = ∠ 3; б) ∠ 8+ ∠ 5=180°; в) ∠ 6= ∠ 7; г) ∠ 8+ ∠ 3=180°; д) ∠ 5= ∠ 3;

е) ∠ 2= ∠ 6; ж) ∠ 1+ ∠ 4=180°; з) ∠ 1+ ∠ 7=180°.

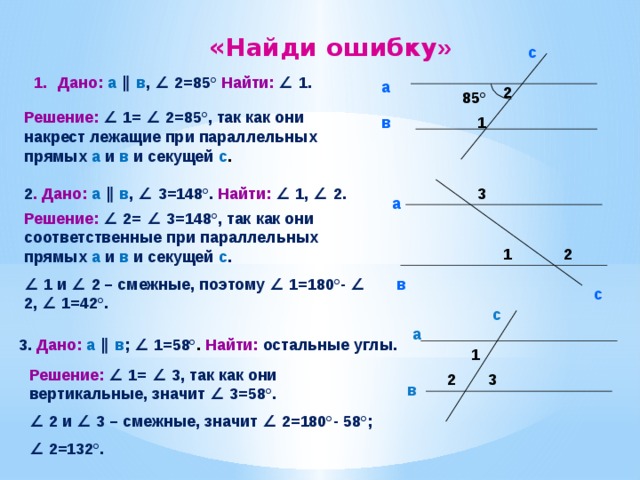
«Найди ошибку »

с

• Дано: а ∥ в , ∠ 2=85° Найти: ∠ 1.

а

2

85 °

Решение: ∠ 1= ∠ 2=85°, так как они накрест лежащие при параллельных прямых а и в и секущей с .

1

в

3

2 . Дано: а ∥ в , ∠ 3=148°. Найти: ∠ 1, ∠ 2.

а

Решение: ∠ 2= ∠ 3=148°, так как они соответственные при параллельных прямых а и в и секущей с .

∠ 1 и ∠ 2 – смежные, поэтому ∠ 1=180°- ∠ 2, ∠ 1=42°.

1

2

в

с

с

а

3. Дано: а ∥ в ; ∠ 1=58° . Найти: остальные углы.

1

Решение: ∠ 1= ∠ 3, так как они вертикальные, значит ∠ 3=58°.

∠ 2 и ∠ 3 – смежные, значит ∠ 2=180°- 58°;

∠ 2=132°.

2

3

в

«Треугольники»

М

А

В

К

О

С

Даны равнобедренные треугольники АВС и МКО с основаниями ВС и КО. Какое условие достаточно добавить, чтобы данные треугольники были равны:

а) по 1 признаку равенства треугольников, если АВ=МК;

в) по 2 признаку равенства треугольников, если ВС=КО .

• Этот треугольник имеет одну замечательную точку.
• Сумма двух углов этого треугольника всегда равна 90 градусов.
• Его стороны являются касательными.
• Его площадь можно найти по формуле S=abc/4R.
• В этом треугольнике ученики всегда с трудом строят высоту .

3)

4)

2)

1)

6)

5)

3 тур

« Признаки»

• Докажите, что четырехугольник – параллелограмм.
• Докажите параллельность прямых.
• Докажите равенство треугольников.
• Докажите подобие треугольников.

B

3)

X

Y

2)

С

В

1 )

O

Z

K

N

А

С

С

К

4)

Д

F

А

Д

А

О

В

4 тур

«Теоремы»

Продолжите теорему (если это возможно):

• Сумма углов треугольника …
• Если две параллельные прямые пересечены секущей, то…
• Если в треугольнике квадрат стороны …
• Средняя линия треугольника…
• Точка пересечения медиан треугольника…
• Вписанный угол …
• Если три угла одного треугольника …
• Отношение площадей двух подобных треугольников равно…
• Если два угла одного треугольника…
• Касательная к окружности перпендикулярна…

« Площади»

5 тур

1) ВД= =6, S=1/2206=60; 2) S=1/2815sin30°=30; 3) S= ; 4) S=1/2ВДАС=1/252=5; 5) S=1/2(5√2)²=25; 6) S=40; 7) S= 10

Соотнести номер решения с номером чертежа

В

ВД=5

АС=2

1)

С

С

В

3)

7)

2)

5√2

3

18

Д

2

В

А

А

В

С

А

А

С

10

4)

В

В

8

5)

6)

6

Д

30°

10

5

В

С

С

А

С

15

А

4

9

Д

А

6 тур

«Аукцион»

Необходимо угадать математическое утверждение.

.

1. Теорема о трех тропинках , ведущих в одну сторону.

В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

2. Теорема о единстве противоположностей.

У параллелограмма противолежащие стороны и углы равны

3. Теорема, не дающая возможности поторговаться.

Сумма углов треугольника равна 180 °

4. Теорема о несправедливом делении: одному – все, другому – половину .

Катет прямоугольного треугольника, лежащий против угла в 30 °, равен половине гипотенузы.

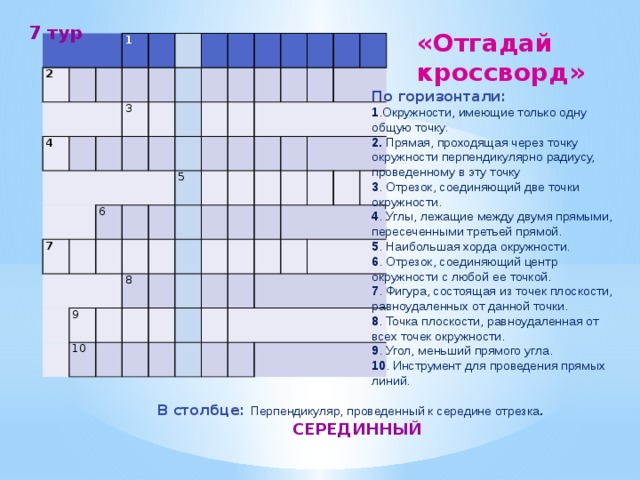
7 тур

«Отгадай кроссворд»

2

1

4

3

7

6

9

5

8

10

По горизонтали:

1 .Окружности, имеющие только одну общую точку.

2. Прямая, проходящая через точку окружности перпендикулярно радиусу, проведенному в эту точку

3 . Отрезок, соединяющий две точки окружности.

4 . Углы, лежащие между двумя прямыми, пересеченными третьей прямой.

5 . Наибольшая хорда окружности.

6 . Отрезок, соединяющий центр окружности с любой ее точкой.

7 . Фигура, состоящая из точек плоскости, равноудаленных от данной точки.

8 . Точка плоскости, равноудаленная от всех точек окружности.

9 . Угол, меньший прямого угла.

10 . Инструмент для проведения прямых линий.

В столбце: Перпендикуляр, проведенный к середине отрезка .

СЕРЕДИННЫЙ

Спасибо

за работу