Презентация «Колебательное движение». 11 класс.

Колебательное

движение

через определённый промежуток времени движение тела повторяется

Свободные колебания

- это колебания под действием внутренних сил после выведения тела из положения равновесия.

Вынужденные колебания

- это колебания под действием внешней периодически изменяющейся силы.

Автоколебания  

- колебания, при которых система имеет запас энергии, расходующейся на совершение колебаний.

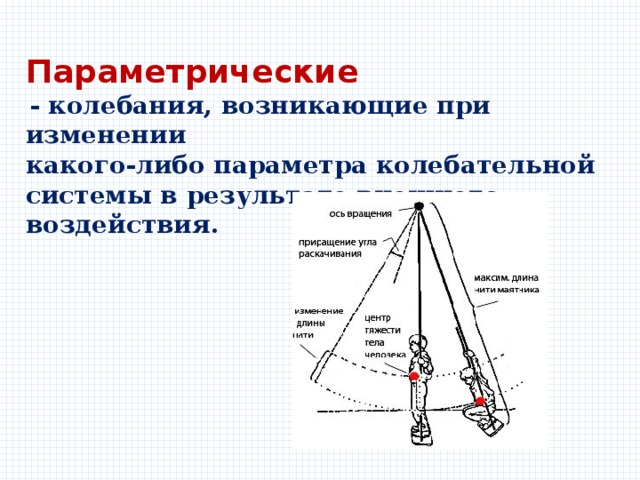
Параметрические

- колебания, возникающие при изменении

какого-либо параметра колебательной системы в результате внешнего воздействия.

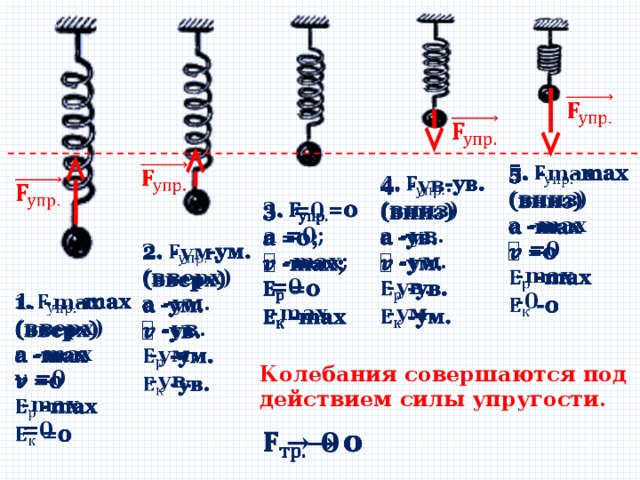
Пружинный маятник

- это груз, прикрепленный к пружине, массой которой можно пренебречь.

5. -max

(вниз)

a -max

𝒗 =0

-max

-0

4. -ув.

(вниз)

a -ув.

𝒗 -ум.

-ув.

-ум.

3. =0

a =0;

𝒗 -max;

=0

-max

2. -ум.

(вверх)

a -ум.

𝒗 -ув.

-ум.

-ув.

1. -max

(вверх)

a -max

𝒗 =0

-max

=0

Колебания совершаются под действием силы упругости.

→ 0

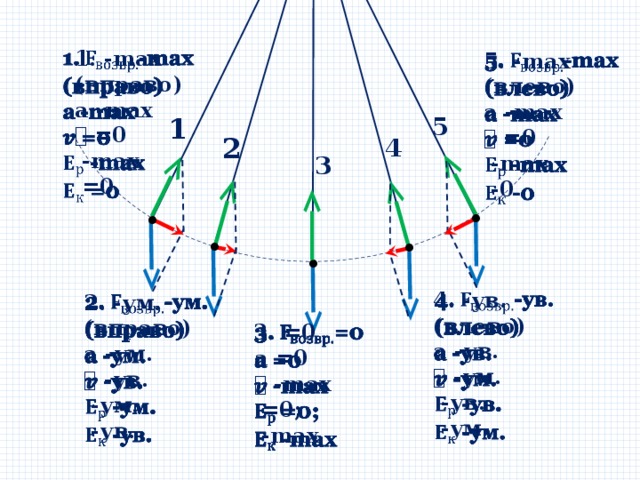
Математический маятник

- это материальная точка, подвешенная на тонкой нерастяжимой и невесомой нити.

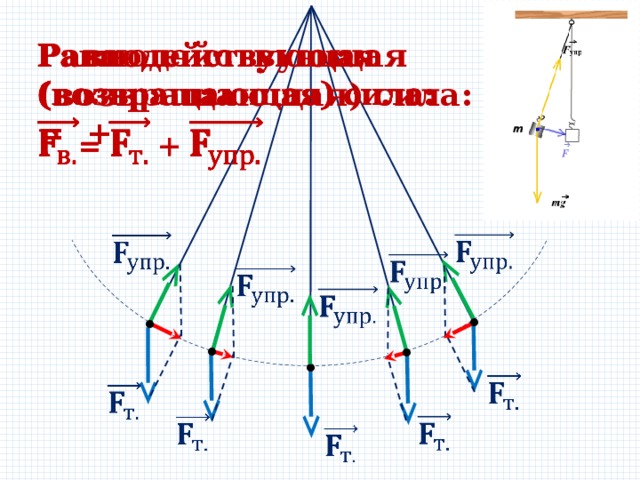
Равнодействующая

(возвращающая) сила:

= +

•

•

•

•

•

1. -max

(вправо)

a -max

𝒗 =0

-max

=0

5. -max

(влево)

a -max

𝒗 =0

-max

-0

1

5

2

4

3

•

•

•

•

•

4. -ув.

(влево)

a -ув.

𝒗 -ум.

-ув.

-ум.

2. -ум.

(вправо)

a -ум.

𝒗 -ув.

-ум.

-ув.

3. =0

a =0

𝒗 -max

=0;

-max

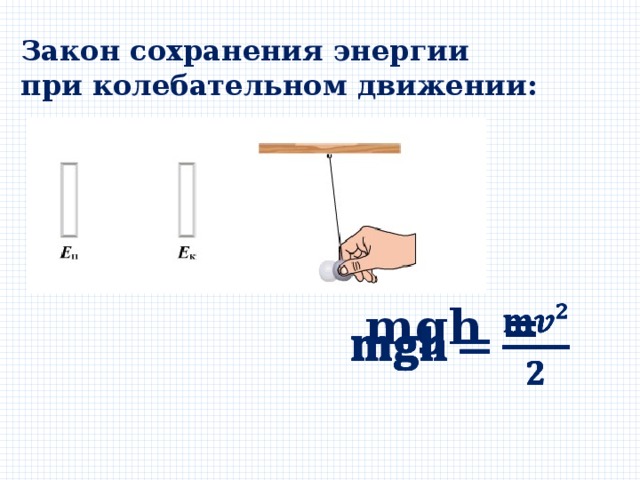
Закон сохранения энергии при колебательном движении:

𝐦 𝐠𝐡 =

Смещение - отклонение тела от положения равновесия в данный момент времени:

х - смещение

СИ: [х] = м

Амплитуда колебаний

- наибольшее (по модулю) отклонение колеблющегося тела от положения равновесия:

А или - амплитуда

СИ: [A] = м

Затухающие колебания

- это колебания, амплитуда которых уменьшается со временем.

Свободные колебания

- затухающие.

Период - это время одного полного колебания:

Т – период СИ: [Т] = с

Частота колебаний  - это число полных колебаний в единицу времени t:

𝛎 – частота СИ: [ 𝛎 ] = Гц

𝚻 =

𝛎 =

𝚻 =

𝛎 =

Циклическая частота  - это число колебаний за 2 𝛑 секунд:

𝞈 – циклическая частота

[ 𝞈 ] =

𝛚 = 2𝞹𝛎 =

Уравнение движения: 

̎ = - 𝙭

𝙠 – жесткость пружины

m - масса груза

Решение уравнения:

𝙭 = соs 𝝎𝙩

𝝎 =

̎ = - 𝙭

𝚻 = 2 𝛑

𝛚 = 2𝞹𝛎 =

Уравнение движения: 

̎ = - 𝙭

g – ускорение свободного падения

𝒍 - длина нити

Решение уравнения:

𝙭 = соs 𝝎𝙩

𝝎 =

̎ = - 𝙭

𝚻 = 2 𝛑

𝛚 = 2𝞹𝛎 =

Гармоническое колебание

- это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

𝙭 = соs(𝝎𝙩 +𝛗₀)

(𝝎𝙩 +𝛗₀) - фаза колебаний

𝛗₀ - начальная фаза

График гармонического колебания

График гармонического колебания

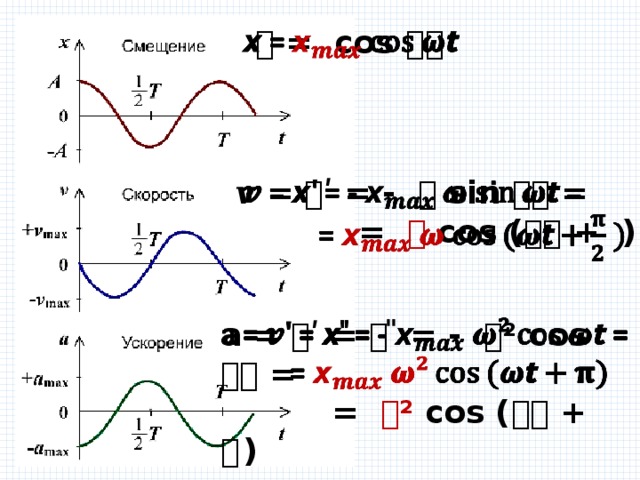
𝙭 = соs 𝝎𝙩

𝒗 = 𝙭ʹ = - 𝝎 sin 𝝎𝙩 =

= 𝝎 cos (𝝎𝙩 + )

a = 𝒗ʹ = 𝙭 ̎ = - 𝝎² cos 𝝎𝙩 =

= 𝝎² cos (𝝎𝙩 + 𝛑)

Вынужденные колебания.

Резонанс:

𝛎 = 𝛎₀

𝛎₀ - частота колебательной системы

𝛎 - частота вынуждающей силы

→ 0

велика

тяжелый язык большого колокола можно раскачать, действуя небольшой силой с частотой, равной собственной частоте колебаний

колокола

необратимые разрушения в различных механических системах

«Написать уравнение»

Материальная точка совершает гармонические колебания, период которых 0,2 с, амплитуда 0,04 м, а начальная фаза . Запишите уравнение этих колебаний, если в начальный момент времени отклонение точки максимально.

«Что можно узнать из уравнения?»

Тело совершает гармонические колебания

по закону х = 0,2 sin 4𝛑t.

Определите амплитуду, период и частоту колебаний.

«Что можно узнать из графика?»

По графику найти амплитуду, период и частоту колебаний.

Написать уравнение гармонических колебаний

Вычислить …

Пружина под действием прикрепленного к ней груза массой 5 кг совершает 45 колебаний в минуту. Найти коэффициент жесткости пружины.

Вычислить …

Математический маятник длиной 99,5 см за одну минуту совершал 30 полных колебаний. Определить период колеба­ния маятника и ускорение свободного падения в том месте, где находится маятник.