Презентация "Определение производной, её геометрический смысл"

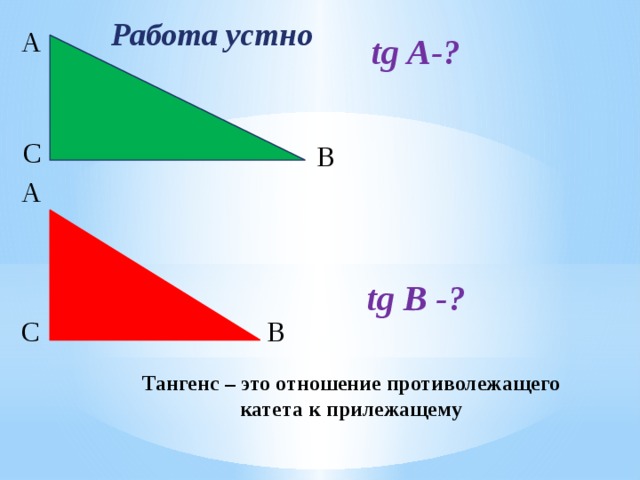
Работа устно

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Работа устно

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции разная. Что касается Матвея — у его дохода она вообще отрицательна

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем? 

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может меняться быстрее или медленнее

Конспект

Производная

— это скорость изменения функции

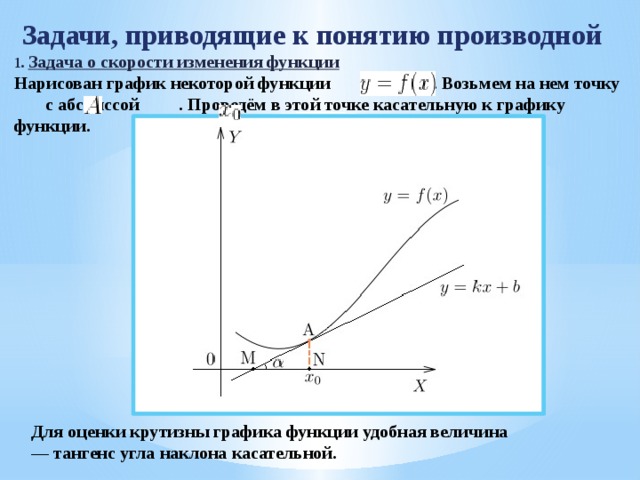
Задачи, приводящие к понятию производной

1. Задача о скорости изменения функции

Нарисован график некоторой функции  . Возьмем на нем точку    с абсциссой  . Проведём в этой точке касательную к графику функции. 

Для оценки крутизны графика функции удобная величина — тангенс угла наклона касательной.

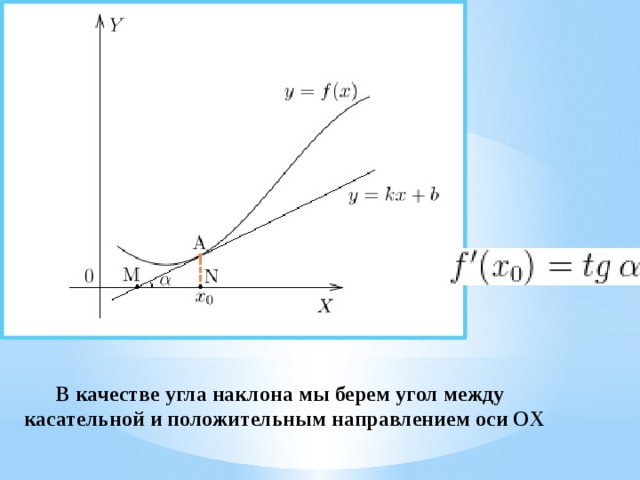
В качестве угла наклона мы берем угол между касательной и положительным направлением оси OX

Конспект

Геометрический смысл производной

Найдем k=tg α

∆ АМN:

˂ АNМ = 90˚,

tgα =

Геометрический смысл производной

Производная функции в точке     равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. 

Производная функции равна тангенсу угла наклона касательной-это есть геометрический смысл производной

Задачи, приводящие к понятию производной

2. Задача о скорости движения

Время в пути равно t

B

А

S

U=S / t

Средняя скорость

ЗАДАЧА . По прямой, на которой заданы начало отсчета, единица измерения(метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой S=s(t), где t – время (в секундах), s(t) – положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).

S(t + Δt)

S(t)

РЕШЕНИЕ. Предположим, что в момент времени t тело находилось в точке M

Δt

М

0

Р

OM=S(t). Дадим аргументу t приращение ∆t и рассмотрим ситуацию в момент времени t + ∆t . Координата материальной точки станет другой, тело в этот момент будет находиться в точке P: OP= s(t+ ∆t) – s(t).

Значит, за ∆t секунд тело переместилось из точки M в точку P.

Имеем: MP=OP – OM = s(t+ ∆t) – s(t).

Полученная разность называется приращением функции: s(t+ ∆t) – s(t)= ∆s. Итак, MP= ∆s (м).

Тогда средняя скорость на промежутке времени [t; t+∆t]:

Конспект

Определение

Производной функции y = f(x) в данной точке x 0 называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что приращение аргумента стремится к нулю.

Обозначение производной:

или

Конспект

Мгновенная скорость

Мгновенная скорость – это средняя скорость на промежутке [t; t+∆t] при условии, что ∆t→0, т. е.:

Алгоритм нахождения производной (по определению)

• Рассмотрим два значения аргумента х 0 и ∆х, где ∆х-приращение аргумента.
• Найдём приращение функции ∆f(x) = f(x 0 + ∆х) – f(x 0 )
• Найдём отношение приращения функции к приращению аргумента
• Вычислим предел этого отношения при ∆х → 0

К онспект

Пример вычисления производной

Решение

Пример вычисления производной

Пример 2.

Найти производную функции y = x

Решение: f(x) = x.

1.Возьмём два значения аргумента x и x + Δx.

2.

3.

4..

Значит, = 1

Пример вычисления производной

Пример 3.

Найти производную функции y = x 2

Решение: f(x) = x 2 .

1.Возьмём два значения аргумента x и x + Δx.

2.

3.

4..

Значит, = 2x

Пример вычисления производной

Пример 4.

Найти производную функции y =

Решение: f(x) = .

1.Возьмём два значения аргумента x и x + Δx.

2.

3.

4..

Значит, = k

Пример вычисления производной

Пример 5.

Найти производную функции y =

Решение: f(x) = .

1.Возьмём два значения аргумента x и x + Δx.

2.

3.

4..

Значит, =

Таблица производных

= 1

Закончи фразу:

• Наш сегодняшний урок был посвящен …
• На уроке я узнал, что …
• На уроке я научился …
• Производная функции в точке равна … касательной, проведенной к графику функции в данной точке
• Скорость изменения функции - это …
• Мне было трудно …

МОЛОДЦЫ!