
Обобщающий урок по теме:
« Тригонометрические формулы »
Учитель математики:
Титова Ирина Александровна

« Величие человека в его способности мыслить . »
Б. Паскаль .

Цель урока:
- Повторение изученного материала

Задачи урока
- Повторить определение синуса, косинуса, тангенса, котангенса числа α;
- Повторить формулы приведения, формулы двойного угла, формулы сложения;
- Повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
- Научить применять полученные знания при решении задач.

Ход урока
- Блиц-опрос
- Закрепление знаний и умений
- Самостоятельная работа (тест)
- Проверка самостоятельной работы
- Это интересно
- Итог урока
- Домашнее задание
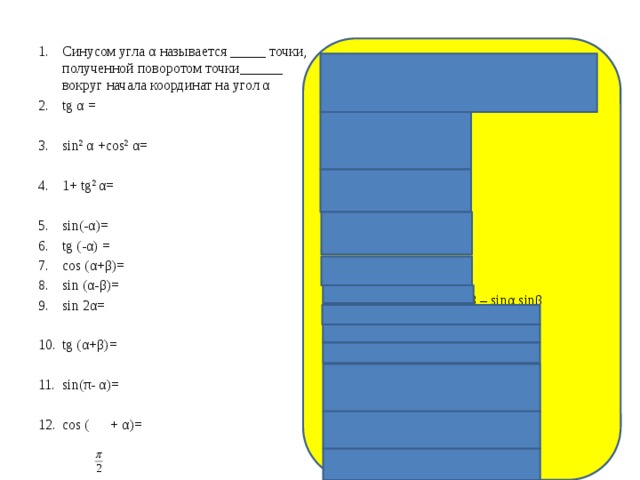
- Синусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
- tg α =
- sin(-α)=
- tg (-α) =
- cos (α+ β)=
- sin (α- β)=
- sin 2α =
- Синусом угла α называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол α
- sin(-α) = - sin α
- tg (-α) = -tg α
- cos (α+ β) = cos α cos β – sin α sinβ
- sin (α- β) = sin α cos β - cos α sin β
- sin 2α = 2sin αcos α
- sin(π- α) =sin α
- cos ( + α) = -sinα

- Косинусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
- ctg α=
- tg α∙ ctg α=
- cos (-α)=
- ctg (-α) =
- cos (α- β)=
- sin (α+ β)=
- cos 2α =
- Косинусом угла α называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол α
- cos (-α) = cos α
- ctg (-α) = -ctg α
- cos (α- β)=cos α cos β +sin α sinβ
- sin (α+ β)= sin α cos β + cos α sin β
- cos 2α =cos 2 α-sin 2 α
- tg 2α =
- cos(π- α)= - cos α

Закрепление знаний и умений
1) Дано:
Найти:
ОТВЕТ:
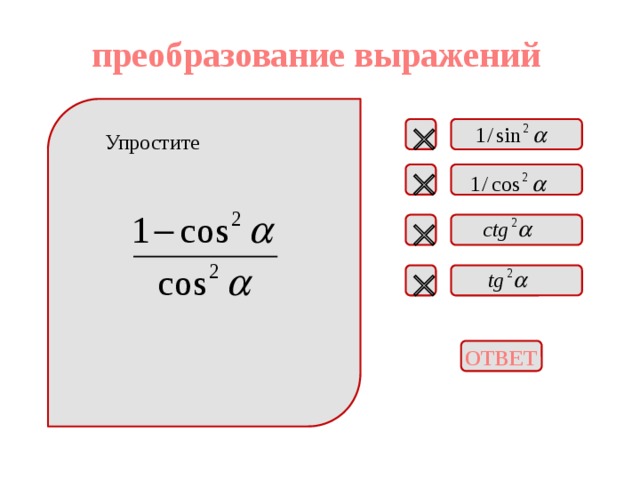
преобразование выражений
Упростите
ОТВЕТ
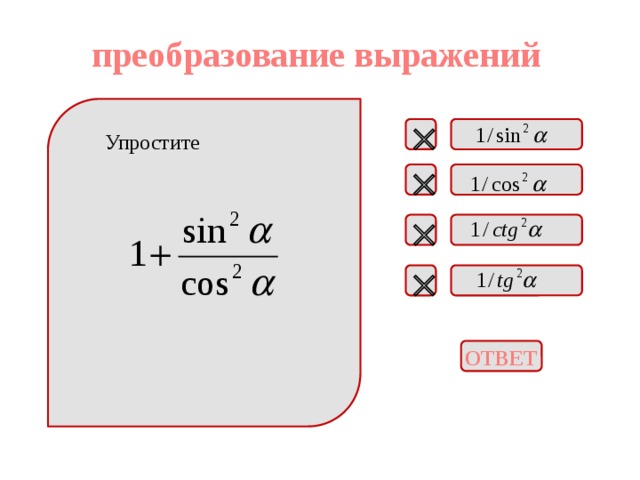
преобразование выражений
Упростите
ОТВЕТ
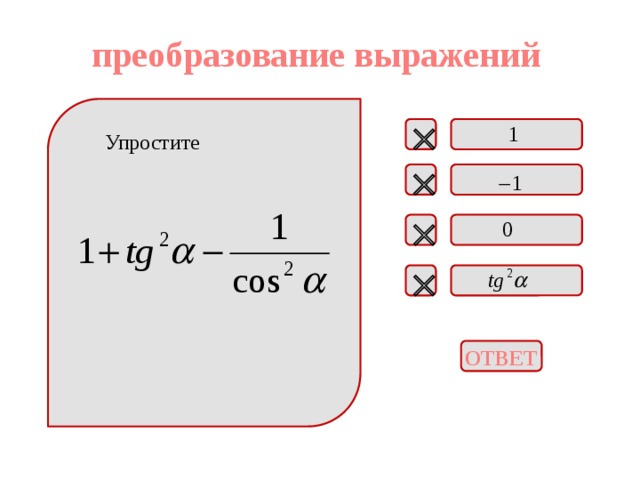
преобразование выражений
Упростите
ОТВЕТ
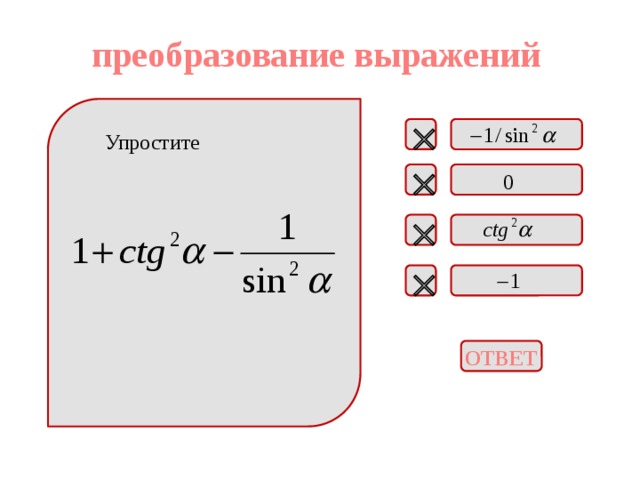
преобразование выражений
Упростите
ОТВЕТ
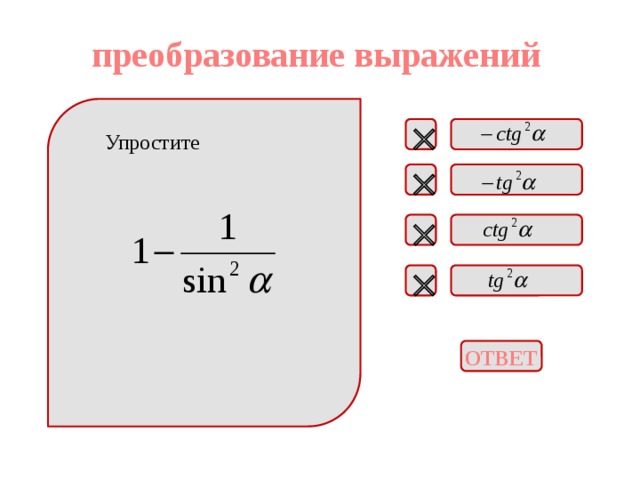
преобразование выражений
Упростите
ОТВЕТ

Упростить выражение
3)
Ответ: -2
4)
Ответ:

Физминутка
«Лови снежинку!»





вариан т 1
1) Найдите значение
а) -2,5; б) 5,5; в) -4,75; г) 3,25.
2) Дано:
Найдите значение:
а) б) в) г)
вариант 2
1) Найдите значение
а) -3,5; б) 9,5; в) -0,5; г) 6,5.
2) Дано:
Найдите значение:
а) б) в) г)
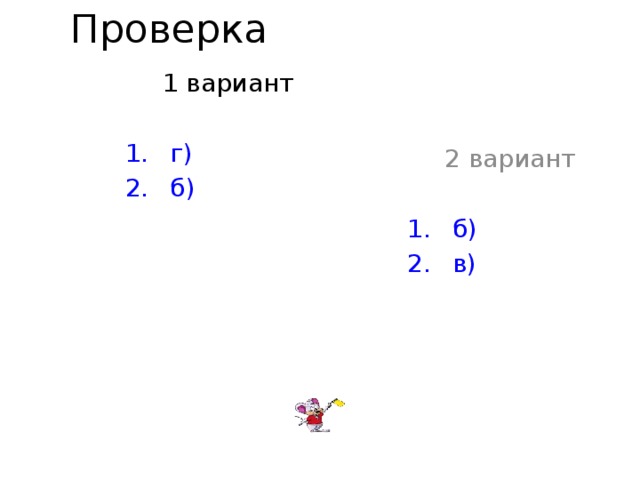
Проверка
1 вариант
2 вариант
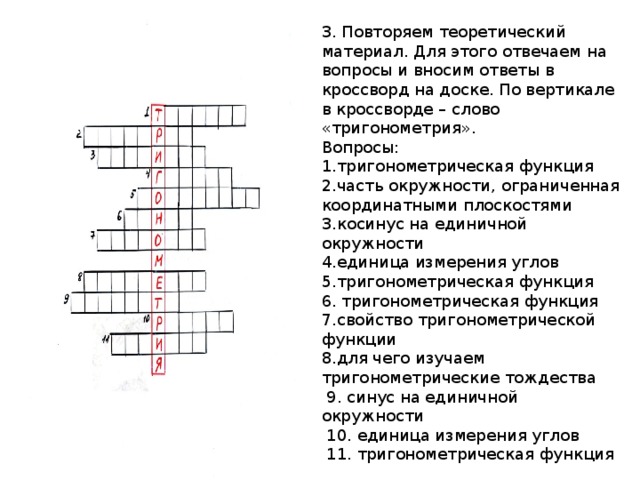
3. Повторяем теоретический материал. Для этого отвечаем на вопросы и вносим ответы в кроссворд на доске. По вертикале в кроссворде – слово «тригонометрия».
Вопросы:
1.тригонометрическая функция
2.часть окружности, ограниченная координатными плоскостями
3.косинус на единичной окружности
4.единица измерения углов
5.тригонометрическая функция
6. тригонометрическая функция
7.свойство тригонометрической функции
8.для чего изучаем тригонометрические тождества
9. синус на единичной окружности
10. единица измерения углов
11. тригонометрическая функция

4 .Далее работаем по рядам (раздать листочки каждому ученику). Каждому ряду свое задание, где нужно записать в таблицу букву, соответствующую точке с заданной радианной мерой.
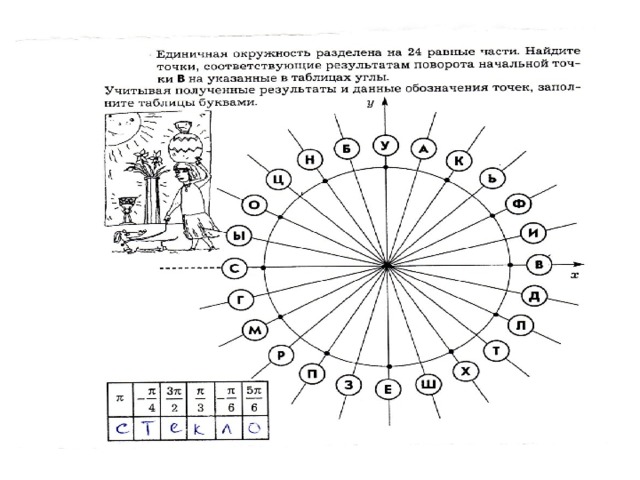
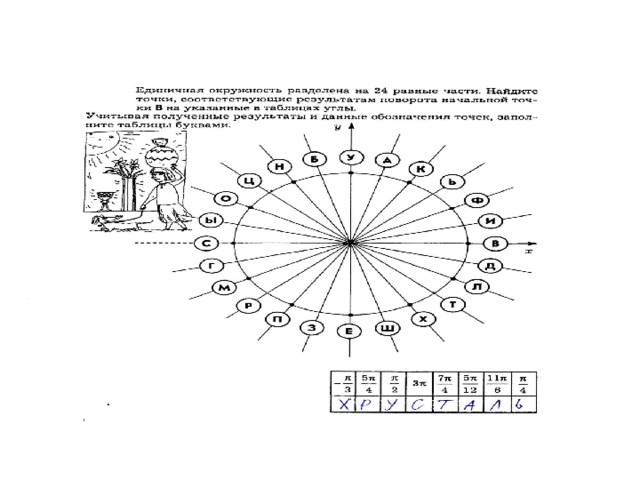
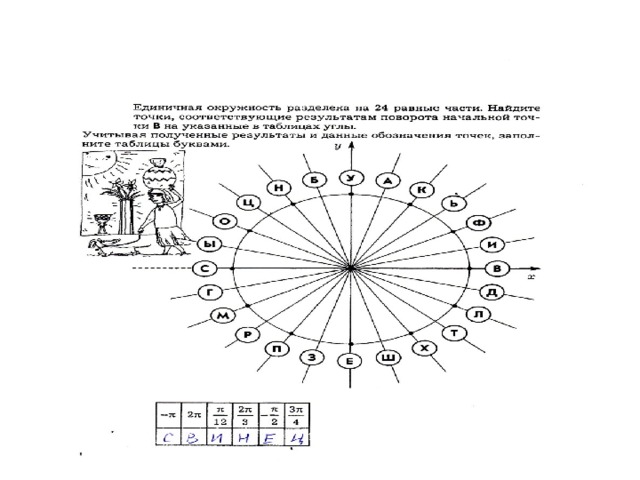

В итоге:
у первого ряда – слово «стекло», у второго ряда – «хрусталь», у третьего – «свинец». Все вместе пытаемся составить предложение с этими словами, используя свои познания по химии. Примерно должно получиться так: «Хрусталь – это стекло с большим содержанием свинца».

Это интересно

Зарождение тригонометрии относится к глубокой древности. Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников».
Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры.
Гиппарх является автором первых тригонометрических таблиц и одним из основоположников астрономии .
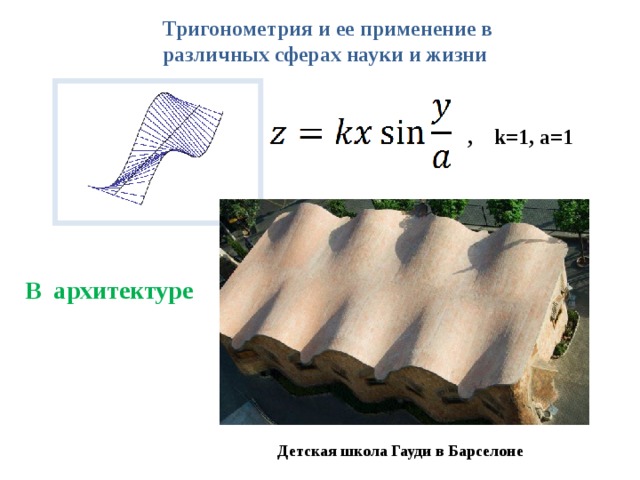
Тригонометрия и ее применение в различных сферах науки и жизни
, k=1, a=1
В архитектуре
Детская школа Гауди в Барселоне

Сантьяго Калатрава Винодельня «Бодегас Исиос»

Феликс Кандела Ресторан в Лос-Манантиалесе

Тригонометрия в физике
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), называются гармоническими колебаниями .
Выражение, стоящее под знаком косинуса или синуса, называется фазой колебания:

Теория радуги
n 1
sin α
=
sin β
n 2
n 1 - показатель преломления первой среды
n 2 - показатель преломления второй среды
α -угол падения, β -угол преломления света
Северное сияние

Тригонометрия в биологии
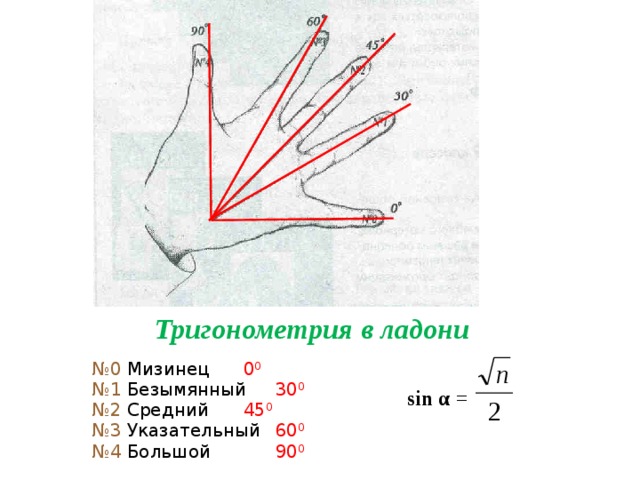
Тригонометрия в ладони
№ 0 Мизинец 0 0
№ 1 Безымянный 30 0
№ 2 Средний 45 0
№ 3 Указательный 60 0
№ 4 Большой 90 0
sin α =
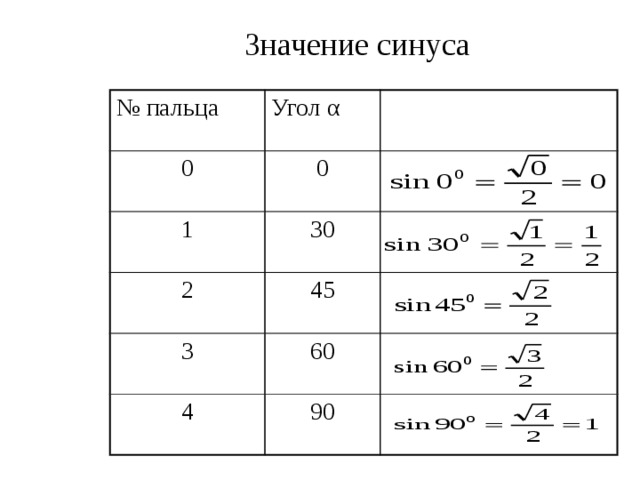
Значение синуса
№ пальца
Угол α
0
1
0
30
2
45
3
60
4
90
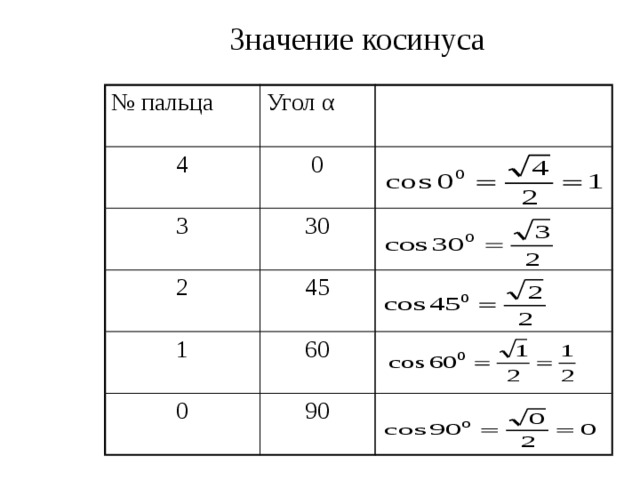
Значение косинуса
№ пальца
Угол α
4
3
0
30
2
45
1
60
0
90

Домашнее задание
Составить кроссворд с тригонометрическими понятиями.
Доказать:

Спасибо за урок
























































