Презентация по теме "Площадь криволинейной трапеции"

Площадь криволинейной трапеции .

у

х

х=а

x=b

Криволинейная трапеция

Криволинейной трапецией называется фигура,

ограниченная графиком непрерывной и не меняющей

на отрезке [а;b] знака функции f(х) , прямыми

х=а, x=b и отрезком [а;b].

У

y = f(x)

b

a

0

Х

Анимация по щелчку мыши

Отрезок [a;b ] называют основанием

этой криволинейной трапеции

3

У=0,5х+1

Криволинейная трапеция

У=-х²+2х

-1

-2

0

2

0

1

0

2

-1

-1

0

Различные виды криволинейных трапеций

x

x

Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие нет?

Задание для заполнения таблицы на следующем слайде

3

2

3

1

Не верно

верно

верно

у

у

у

y = f(x)

y = f(x)

3

y = f(x)

У=1

0

х

0

х

0

х

6

4

5

y = f(x)

у

у

у

y = f(x)

y = f(x)

У=3

Для проверки триггер – нажать на кнопку с № ответа (верно/неверно)

0

х

0

х

0

х

Не верно

верно

Не верно

7

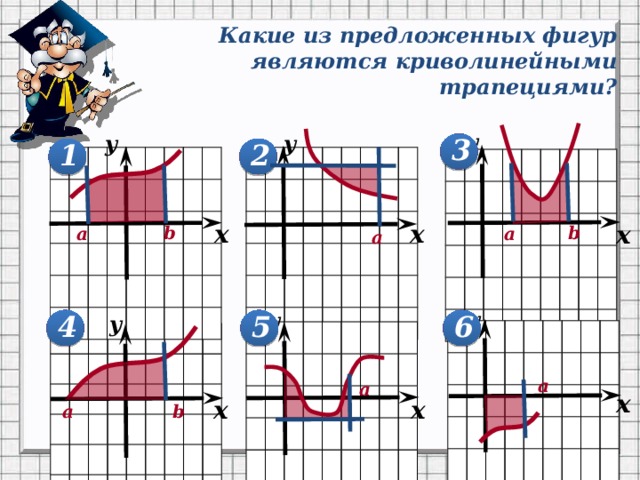
Какие из предложенных фигур являются криволинейными трапециями?

y

y

y

3

2

1

x

x

x

b

b

a

a

a

y

y

6

4

5

y

a

a

x

x

x

b

a

y=f(x)

y=f(x)

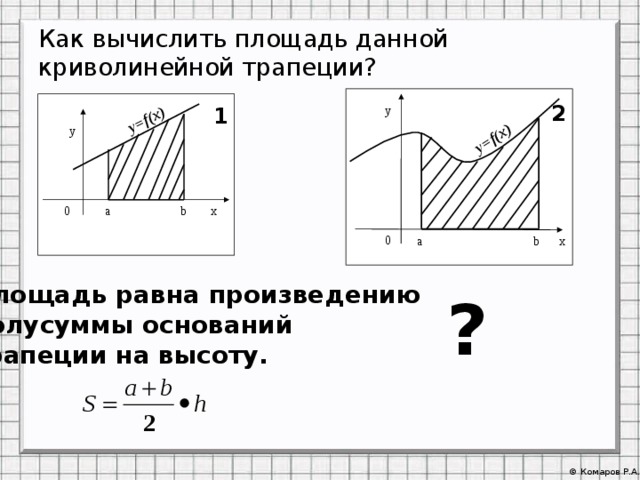
Как вычислить площадь данной криволинейной трапеции?

2

y

1

y

b

а

x

0

0

а

b

x

Площадь равна произведению

полусуммы оснований

трапеции на высоту.

?

© Комаров Р.А.

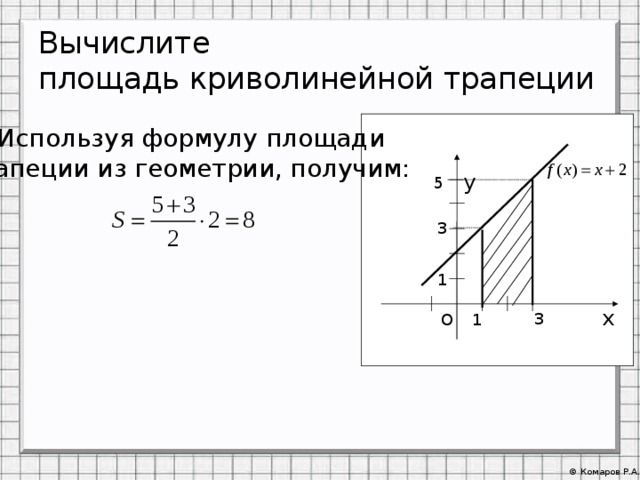
Вычислите площадь криволинейной трапеции

1) Используя формулу площади

трапеции из геометрии, получим:

у

5

3

1

х

3

1

О

© Комаров Р.А.

Фигура, ограниченная прямыми х=а, х=b, графиком непрерывной и неотрицательной на [a; b] функции y=f(x) и осью Ох, называется криволинейной трапецией

y

y=f(x)

S

x

a

b

[a; b] – основание криволинейной трапеции

y=f(x)

y=f(x)

Как вычислить площадь данной криволинейной трапеции?

2

y

1

y

x

b

а

0

0

x

b

а

Площадь равна произведению

полусуммы оснований

трапеции на высоту.

?

© Комаров Р.А.

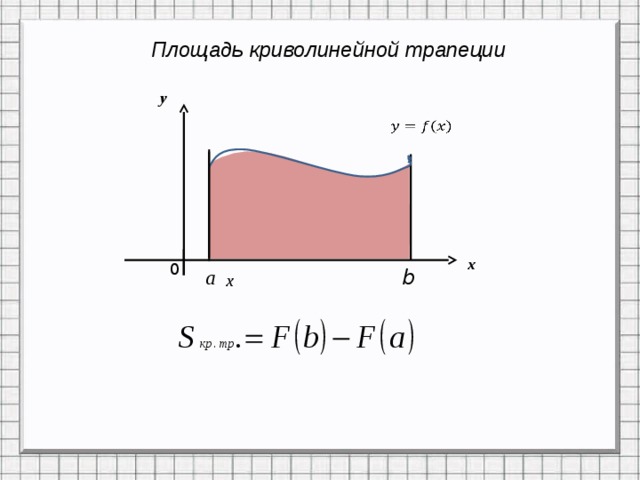
Площадь криволинейной трапеции

у

х

0

b

a

x

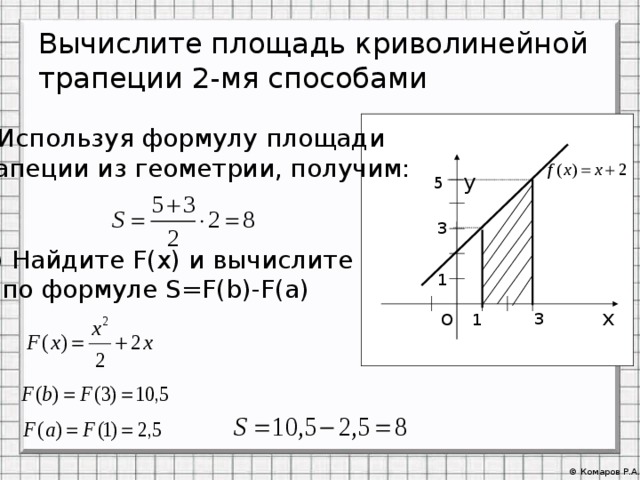
Вычислите площадь криволинейной трапеции 2-мя способами

1) Используя формулу площади

трапеции из геометрии, получим:

у

5

3

2) Найдите F(x) и вычислите

S по формуле S=F(b)-F(a)

1

х

3

О

1

© Комаров Р.А.

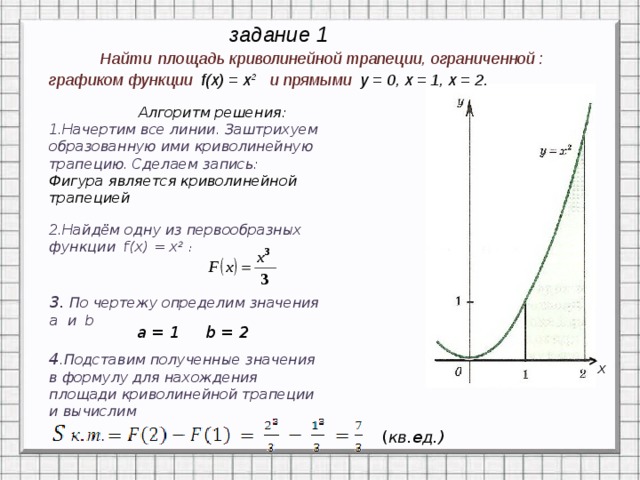
задание 1

Найти площадь криволинейной трапеции, ограниченной :

графиком функции f(x) = х 2 и прямыми у = 0, х = 1, х = 2.

,

Алгоритм решения:

1.Начертим все линии. Заштрихуем образованную ими криволинейную трапецию. Сделаем запись:

Фигура является криволинейной трапецией

2.Найдём одну из первообразных функции f(x) = х 2 :

3. По чертежу определим значения

a и b

a = 1 b = 2

4 .Подставим полученные значения в формулу для нахождения площади криволинейной трапеции и вычислим

х

( кв.ед.)

x = 2

Найти S криволинейной трапеции, ограниченной графиком функции y = (x- 1 ) 2 , осью Ox и прямой x =2 .

Анимация по щелчкам –построение графика – сдвиг оси ОУ на 1 влево

14

I

I

Найти площадь криволинейной трапеции,

изображенной на рисунке

1

y =sinx

0

-1