Презентация пропорции

Учитель математики «Снагостской СОШ» Рогозин П.А.

Математика – основа и царица всех наук, И тебе с ней подружиться я советую, мой друг. Ее мудрые законы если будешь выполнять, Свои знанья приумножишь, Станешь ты их применять. Сможешь по морю ты плавать, Сможешь в космосе летать. Дом построить людям сможешь: Будет он сто лет стоять. Не ленись, трудись, старайся, Познавая соль наук. Все доказывать пытайся, Но не покладая рук.

Повторим!

• Что такое пропорция?
• Как называются числа х и у в пропорции х : а = в : у ?
• Как называются числа а и в в пропорции х : а = в : у ?

Пропорция – это равенство двух отношений

Крайние члены пропорции

Средние члены пропорции

• Произведение крайних членов пропорции равно произведению средних членов пропорции

Сформулируйте основное свойство пропорции.

И з чисел 10 ; 5 ; 6 и 3 составьте восемь различных верных пропорций .

Ответ:

3 : 5 = 6 : 10

5 : 10 = 3 : 6

10 : 6 = 5 : 3

6 : 10 = 3 : 5

6 : 3 = 10 : 5

5 : 3 = 10 : 6

3 : 6 = 5 : 10

10 : 5 = 6 : 3

Решите уравнения, используя основное свойство проп орции.

8х = 16*3

х = 6

↓↓

больше

↓↓

больше

↓↓

больше

↑ ↓

меньшее

↑ ↓

меньше

↑ ↓

меньше

Задача 1. Лыжник прошел расстояние 8,4 км за 1,5 ч. Какое расстояние пройдет он за 2,5 ч, если будет идти с той же скоростью?

Решение : Пусть за 2,5 ч лыжник пройдет x км.

Расстояние Время

8,4 км 1,5 ч

x км 2,5 ч

Т.к. время и расстояние прямо пропорциональные величины, составим пропорцию:

Ответ: 14 км

Задача2. Два каменщика могут сложить стену за 15 дней. За сколько дней могут сложить эту стену 5 каменщиков при той же производительности труда?

Решение: Пусть 5 каменщиков сложат стену за х дней .

Число рабочих Время

2 каменщика 15 дней

5 каменщиков x дней

Т.к. число рабочих и время обратно пропорциональные величины, составим пропорцию:

Ответ: 6 дней

Задача3. Один велосипедист проехал расстояние 24 км со скоростью 12 км/ч. Какое расстояние проедет за это время другой велосипедист, скорость которого 10,5 км/ч?

Решение: Пусть второй велосипедист за это же время пройдет x км.

Скорость Расстояние

1 велосипедист 12 км/ч 24 км

2 велосипедист 10,5 км/ч x км

Т.к. скорость и расстояние прямо пропорциональные величины, составим пропорцию: 12:10,5=24: Х

Ответ: 21 км

Задача4. Теплоход на подводных крыльях прошел расстояние между пристанями со средней скоростью 60 км/ч за 2,5 ч. За сколько времени пройдет это расстояние теплоход, если будет идти со скоростью 50 км/ч?

Решение: Пусть с новой скоростью теплоход пройдет

расстояние за x ч .

Скорость Время

60 км/ч 2,5 ч

50 км/ч x ч

Т.к. скорость и время обратно пропорциональны, составим пропорцию: 60:50 = x :2,5

Ответ: 3 часа

Задача: Всадник, двигаясь со скоростью 18 км/ч, преодолел некоторое расстояние за 1 ч 30 мин. За какое время проедет это расстояние автомобиль, скорость которого 120 км/ч ?

90

1 ч 30 мин = ___ мин

Решение :

Пусть время затраченное автомобилем x мин.

Скорость Время

Всадник

Автомобиль

18 км/ч 90 мин

120 км/ч х мин

Составим пропорцию:

18 : 120 = х : 90

Ответ:13,5 мин.

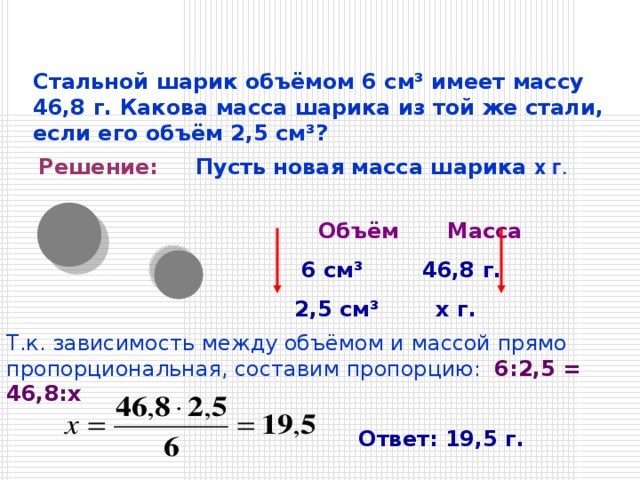
Стальной шарик объёмом 6 см ³ имеет массу 46,8 г. Какова масса шарика из той же стали, если его объём 2,5 см ³ ?

Решение: Пусть новая масса шарика х г .

Объём Масса

6 см ³ 46,8 г.

2,5 см ³ x г.

Т.к. зависимость между объёмом и массой прямо пропорциональная, составим пропорцию: 6:2,5 = 46,8: x

Ответ: 19,5 г.

Итог урока.

• Какие величины называют прямо пропорциональными?
• Приведите примеры прямо пропорциональных величин.
• Какие величины называют обратно пропорциональными?
• Приведите примеры обратно пропорциональных величин.
• Приведите примеры величин, у которых зависимость не является ни прямо, ни обратно пропорциональной.

Домашнее задание:

п. 22

№ 811,812.