Презентация "Решение целых уравнений"

Муниципальное общеобразовательное учреждение

лицей №5 имени Ю.А. Гагарина

Методы решения целых и дробно-рациональных уравнений.

Автор:

Таболаева Марина Васильевна -учитель математики МОУ лицея №5 им.Ю.А.Гагарина Волгограда

Волгоград 2016

Цель урока

• Изучить основные методы решения целых и дробно-рациональных уравнений.
• Показать на примерах различные комбинации этих методов для решения уравнений.
• Узнать историю появления рациональных уравнений.

Актуальность темы

И в школьной программе и в олимпиадах часто встречаются уравнения, для решения которых не достаточно простых вычислений или выделения дискриминанта, а нужны порой творческие комбинации особых методов решений.

Данную презентацию можно использовать в качестве пособия при отработке решений целых и рациональных уравнений.

Определения

• P(x) = a 0 x n + a 1 x n – 1 + a 2 x n – 2 + … + a n – 1 x + a n , где n — натуральное, a 0 , a 1 ,…, a n — некоторые действительные числа, называется целым рациональным выражением.
• Уравнение вида P(x) = 0, где P(x) — целое рациональное выражение, называется целым рациональным уравнением.
• Дробно-рациональным уравнением называется уравнение вида P(x)/Q(x)=0, где P(x) и Q(x) - рациональные выражения

Основные методы решения целых и дробно-рациональных уравнений

• Группировка
• Разложение на множители
• Введение новой переменной
• Метод неопределенных коэффициентов
• Графический метод
• Выделение целой части

Пример

Уравнение №1

1 . (x-1)(x-7)(x-4)(x+2)=40

В этом виде уравнения в левой части стоит произведение четырех скобок, а в правой – число.

1. Сгруппируем скобки по две так, чтобы сумма свободных членов была одинаковой.

В нашем уравнении первую скобку с третьей,  а вторую с четвертой, так как

(-1)+(-4)=(-7)+2

2. Перемножим их.

3. Введем новую переменную.

Получаем уравнение

Раскрывая скобки получаем квадратное уравнение относительно t, получаем :

t1=16, t2=-6

и подставляем t в равенство  

решаем два квадратных уравнений относительно х

Ответ:   

Пример

Заметим, что в каждой скобке коэффициент при х в квадрате  и свободный член одинаковые. Вынесем из каждой скобки множитель х

Так как х=0 не является корнем исходного уравнения, разделим обе части уравнения на х в квадрате. Получим:

Теперь можем ввести замену переменной:

Получим уравнение: 

t1=1, t2=-4

Ответ:  

Уравнение №2

2 .  

Уравнение этого типа похоже на предыдущее с одним отличием: в правой части уравнения стоит произведение числа на х в квадрате.

1. Группируем скобки по две так, чтобы произведение свободных членов было одинаковым .

2. Перемножаем каждую пару скобок.

3. Из каждого множителя выносим за скобку х.

4. Делим обе части уравнения на х в квадрате

5. Вводим замену переменной.

В этом уравнении сгруппируем первую скобку с четвертой, а вторую с третьей, так как :

Пример

Уравнение №3

Теперь можем ввести замену переменной:

Получим уравнение относительно переменной t:

Полученное уравнение приводим к общему знаменателю, имея в виду что t не равно 0 и 2, получаем квадратное уравнение относительно t.

t1=1 и t2=8 . подставляем эти значения в равенство:

И решаем два квадратных уравнения относительно х

Ответ:

3 .  

Заметим, что в знаменателях обоих дробей стоят квадратные трехчлены, у которых старший коэффициент и свободный член одинаковые. Вынесем, как и в уравнении №2, х за скобку. Получим:

Разделим числитель и знаменатель каждой дроби на х:

Пример

Уравнение №4

4 .  

Коэффициенты уравнения симметричны относительно центрального. Такое уравнение называется  возвратным .

Чтобы его  решить,

1. Разделим обе части уравнения на х  (Мы можем это сделать, так как х=0 не является корнем уравнения.) Получим:

2. Сгруппируем слагаемые таким образом:

3. В каждой группе вынесем за скобку общий множитель:

4. Введем замену: 

5. Выразим через t выражение 

Отсюда 

Получим уравнение относительно t:

Решаем его и находим, что t1=10/3, а t2=2,5.

Подставляем в

И находим х

Ответ:  

Однородные уравнения

Пример.

Однородное уравнение

Уравнение №5

Получим квадратное уравнение:

Найдем значения t

t1=-5/4 t2=7,75

Подставим в

И найдем корни уравнения

Ответ:

Пример. Метод симметризации.

Уравнение №6

6.

Это уравнение имеет такую структуру:

Решается с помощью введения переменной:

В нашем уравнении 

,тогда 

Введем заменув уравнение:

Теперь возведем каждую скобку в четвертую степень, используя треугольник Паскаля:

Упростим выражение и получим биквадратное уравнение относительно  t:

Введем замену y=

Получим квадратное уравнение:

Найдем значения y

y1= y2=

y может принимать только положительные значения, следовательно у2 не подходит, находим t

t=

Вернемся к переменной х

х=t-2

Ответ: -2

Треугольник Паскаля

Пример. Выделение полного квадрата.

Уравнение №7

7 . 

Это уравнение имеет такую структуру:

Чтобы его решить, нужно в левой части уравнения выделить полный квадрат.

Для этого нужно прибавить или вычесть удвоенное произведение. Тогда мы получим квадрат суммы или разности. Для удачной замены переменной это имеет определяющее значение.

Начнем с нахождения удвоенного произведения:

Теперь прикинем, что нам удобнее иметь – квадрат суммы или разности. Рассмотрим, для начала сумму выражений:

Это выражение в точности равно удвоенному произведению. Тогда, чтобы в скобках получить квадрат суммы, нужно прибавить и вычесть удвоенное произведение:

Введем замену:

Получим квадратное уравнение

Решаем его и возвращаемся к исходной переменной х

Ответ:

Пример.

Уравнение №8

8.

Подставляя в уравнение делители свободного члена -3, получаем два корня: и, значит можем представить это уравнение в виде:

Находим коэффициенты p и q из равенства

Открываем скобки и получаем q = 1

p = -4.

Следовательно исходное уравнение приводится к виду:

Приравнивая третью скобку к 0, находим оставшиеся корни уравнения

,

Ответ: , ,

Пример. Графический метод

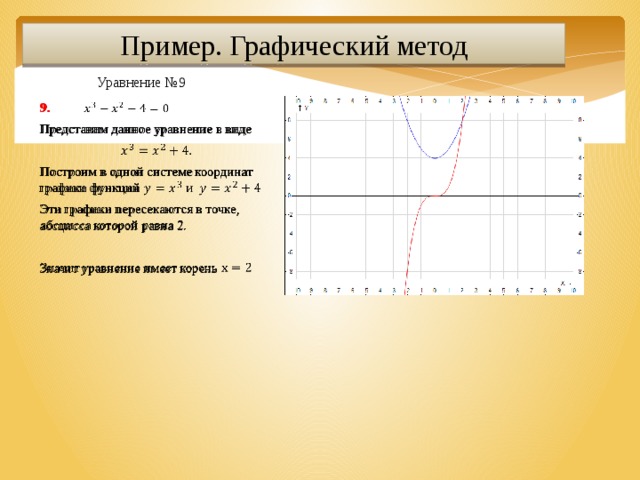
Уравнение №9

9.

Представим данное уравнение в виде

Построим в одной системе координат графики функций

Эти графики пересекаются в точке, абсцисса которой равна 2.

Значит уравнение имеет корень

Уравнения для самостоятельного решения

2 формулы, которые выражали бы корни уравнения через его коэффициенты с помощью четырех арифметических действий – сложения, вычитания, умножения, деления – и извлечения корней или радикалов, то есть, говоря более кратко, решали бы уравнение в радикалах. Однако «мрачное средневековье» оказалось как нельзя более мрачным и в отношении обсуждаемой задачи – в течение целых семи столетий требуемых формул никто не нашел. Только в 16 веке итальянским математикам удалось продвинуться дальше – найти формулы для n=3 и n=4. " width="640"

Из истории рациональных уравнений

Уже в древности люди осознали, как важно научиться решать алгебраические уравнения вида

а 0 х n +а 1 х n-1 +…+а n =0

— ведь к ним сводятся очень многие и очень разнообразные вопросы практики и естествознания (конечно, здесь можно сразу предполагать, что а 0  0, так как иначе степень уравнения на самом деле не n, а меньше).

Уместно напомнить, что сам термин «алгебра» происходит от названия сочинения Мухаммеда аль-Хорезми, (то есть Мухаммеда из Хорезма) «Аль-джебр аль-мукабала», в котором излагались решения такого уравнения при n=1 и n=2.

Многим, разумеется, приходила в голову заманчивая мысль найти и для любой другой степени n2 формулы, которые выражали бы корни уравнения через его коэффициенты с помощью четырех арифметических действий – сложения, вычитания, умножения, деления – и извлечения корней или радикалов, то есть, говоря более кратко, решали бы уравнение в радикалах.

Однако «мрачное средневековье» оказалось как нельзя более мрачным и в отношении обсуждаемой задачи – в течение целых семи столетий требуемых формул никто не нашел. Только в 16 веке итальянским математикам удалось продвинуться дальше – найти формулы для n=3 и n=4.

Из истории рациональных уравнений

Сегодня ученый, сделав какое-либо открытие, стремится поскорее рассказать о нем на научной конференции, опубликовать статью в научном журнале. Совсем не так было в 16 веке. Сделав открытие, средневековый мыслитель скрывал его как можно дольше, оставаясь, так сказать, единственным владельцем того, чего нет ни у кого другого. Так было и в этом случае.

Для математиков того времени существовало не одно уравнение третьей степени

х 3 +рх 2 +qx+r=0,

а несколько, из которых главнейшими были три:

х 3 +рх=q

х 3 =рх+q

х 3 +рх 2 =q

А почему же не одно? Потому что в те времена рассматривались лишь уравнения с положительными коэффициентами. Первыми из них было решено уравнение х 3 +рх=q. Это удалось сделать итальянскому математику Сципиону Даль Ферро (1465-1526).

Даль Ферро не опубликовал найденного им способа, но некоторые из его учеников знали об этом открытии, и вскоре один из них, Антонио Фиор, решил им воспользоваться.

Из истории рациональных уравнений

В те годы были распространены публичные диспуты по разного рода научным вопросам. Победители таких диспутов обычно получали неплохое вознаграждение, от исхода научного поединка нередко зависела судьба ученого. Фиор рассчитывал на победу в любом диспуте, ведь он знал то, чего не знали другие (правда, он не знал много, что знали другие).

В это время в итальянском городе Верона жил небогатый учитель математики Никколо Тарталья (1499-1557). Тарталья был очень талантливым человеком и сумел в 1535 году заново открыть прием, изобретенный Сципионом Даль Ферро.

Состоялся поединок между Фиором и Тартальей. По условию, соперники обменялись тридцатью задачами, на решение которых отводилось шестьдесят дней. Но так как Фиор знал по существу только одну задачу и был уверен, что какой-то учитель решить ее не сможет, то все его тридцать задач оказались однотипными. Тарталья был хорошо подготовлен к их решению и справился со всеми тридцатью задачами за два часа. Фиор же не смог решить ни одной из задач, предложенных его противником. Победа прославила Никколо Тарталью на всю Италию, но вопрос о решении уравнений третьей степени еще не был решен до конца.

Источники

• Интернет ресурсы:

http:// webmath.exponenta.ru

http:// www.math24.ru

http:// ru.wikipedia.org

http:// ege-ok.ru

http:// 5ballov.qip.ru

• Учебник Адгебра 9кл (Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. Изд. «Мнемозина», Москва 2011)

СПАСИБО

ЗА

ВНИМАНИЕ