Применение геометрии в жизни

МБОУ «Средняя общеобразовательная школа №29» с углубленным изучением отдельных предметов города Ставрополя.

Применение геометрии в жизни.

Работу выполнил:

Силин Илья

школа №29, 9 класс

Научный руководитель:

Емец С.В.,

учитель математики

г.Ставрополь, 2020г.

Содержание

1. Введение

2. Измерение высоты дерева.

2.1 По длине тени.

2.2 Измерение высоты дерева при помощи простого

булавочного прибора.

2.3 Измерение высоты дерева, не приближаясь к дереву.

3. Геометрия у реки.

3.1 Измерение ширины реки.

3.2 Измерение глубины пруда.

4. Заключение.

5. Список литературы.

Введение

Геометрия – одна из самых древних наук. В переводе с греческого слово «геометрия» означает «землемерие» («гео» - земля, «метрео» - мерить). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, геометрия возникла на основе практической деятельности людей и в начале своего развития служила преимущественно практическим целям.

Целью работы служит рассмотреть применение геометрии на практике.

В своей работе рассматриваю следующие вопросы:

1. Измерение высоты дерева. (несколькими способами)

2. Измерение ширины, глубины реки.

Измерение высоты дерева

1. По длине тени

Существует множество различных способов измерения высоты дерева, не срубая его и не взбираясь на верхушку, при помощи весьма незамысловатых приборов и даже без всяких приспособлений.

Самый лёгкий и самый древний способ – без сомнения, тот, которым греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался её тенью. Фалес, - говорит предание, - избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени. А чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было узнать некоторые геометрические свойства треугольника, - именно следующие два:

1) что углы при основании равнобедренного треугольника равны, и обратно – что стороны, лежащие против равных углов треугольника, равны между собою;

2) что сумма углов всякого треугольника равна двум прямым угла.

Только вооружённый этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и следовательно, вершина пирамиды, середина её основания и конец её тени должны обозначить равнобедренный треугольник.

Способ Фалеса в указанном виде применим не всегда, так как солнце у нас низко стоит над горизонтом, и тени бывают равны высоте отбрасывающих их предметов лишь в околополуденные часы летних месяцев.

Нетрудно, однако, изменить этот способ так, чтобы в солнечный день можно было пользоваться любой тенью, какой бы длины она ни была. Измерив, кроме того, и свою тень или тень какого-нибудь шеста, вычисляют искомую высоту из пропорции:

AС:МК=BC:РК

т.е. высота дерева во столько же раз больше вашей собственной высоты, во сколько раз тень дерева длиннее вашей тени. Это вытекает, конечно, из геометрического подобия треугольников АВС и МРК.

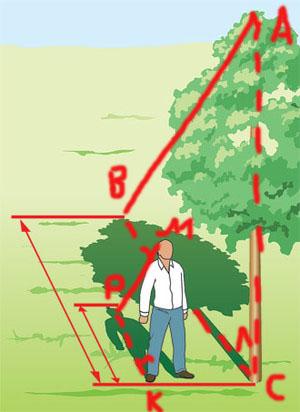Рис.1 Измерение высоты дерева.

2. Измерение высоты дерева при помощи простого булавочного прибора

Вполне возможно обойтись при измерении высоты и без помощи теней. Таких способов много; начнём с двух простейших.

Прежде всего мы можем воспользоваться свойством равнобедренного треугольника, обратившись к услугам весьма простого прибора, который легко изготовить из дощечки и трёх булавок. На дощечке любой формы, даже на куске коры, если у него есть плоская сторона, намечают три точки – вершины равнобедренного треугольника – и в них втыкают торчком по булавке. (рис.2) Пусть у вас нет под рукой чертёжного треугольника для построения прямого угла, нет циркуля для отложения равных сторон. Перегните тогда любой лоскут бумаги один раз, а затем поперёк первого сгиба ещё раз так, чтобы обе части первого сгиба совпали, - и получите прямой угол. Та же бумага пригодится вместо циркуля, чтобы отмерить равные расстояния.

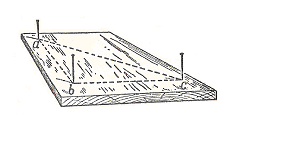Рис.2 Булавочный прибор для измерения высот.

Обращение с ним не сложнее изготовления. Отойдя от измеряемого дерева, держите прибор так, чтобы один из катетов треугольника был направлен отвесно, для чего можете пользоваться ниточкой с грузиком, привязанной к верхней булавке.

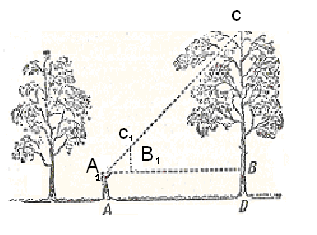
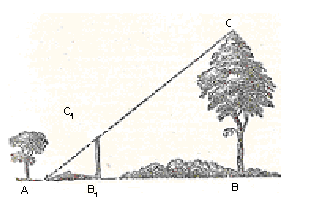
Рис.3 Схема применения булавочного прибора. Рис.4

Приближаясь к дереву или удаляясь от него, вы всегда найдёте такое место А (рис.3), из которого, глядя на булавки А₁ и С₁ , увидите, что они показывают верхушку С дерева: это значит, что продолжение гипотенузы

А₁С₁ проходит через точку С. Тогда, очевидно, расстояние А₁В равно СВ, так как угол а=45⁰.

Следовательно, измерив расстояние А₁В и прибавив ВD, т.е. возвышение А₁А глаза над землёй, получите искомую высоту дерева.

По другому способу вы обходитесь даже и без булавочного прибора. Здесь нужен шест, который вам придётся воткнуть в землю так, чтобы выступающая часть как раз равнялась вашему росту. Место для шеста надо выбрать так, чтобы, лежа, как показано на рис.4, вы видели верхушку дерева на одной прямой линии с верхней точкой шеста. Так как треугольник АВ₁С₁ – равнобедренный и прямоугольный, то угол А=45⁰ и, следовательно, АВ равно ВС, т.е. искомый высоте дерева.

3. При помощи приятеля и карандаша

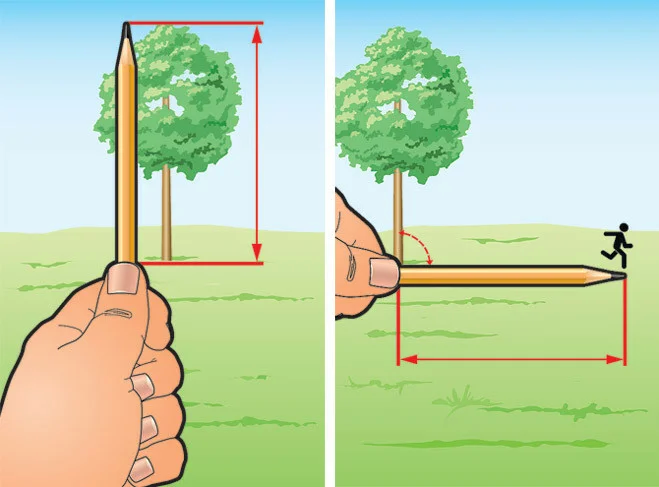
Встань от дерева на такое расстояние, чтобы видеть его целиком – от основания до верхушки. Рядом со стволом установи приятеля. Вытяни перед собой руку с карандашом, зажатым в кулаке.

Прищурь один глаз и подведи кончик грифеля к вершине дерева. Теперь перемести ноготь большого пальца так, чтобы он оказался под основанием ствола.

Поверни кулак на 90 градусов, чтобы карандаш оказался расположен параллельно земле. При этом твой ноготь должен все так же оставаться в точке основания ствола.

Крикни своему верному другу, чтобы он отбежал от зеленого друга. Когда твой приятель достигнет точки, на которую указывает острие карандаша, подай сигнал, чтобы он остановился.

Измерь расстояние от ствола до места, где застыл твой приятель. Оно будет равняться высоте дерева.

4. Измерение высоты дерева, не приближаясь к дереву.

Рис. 5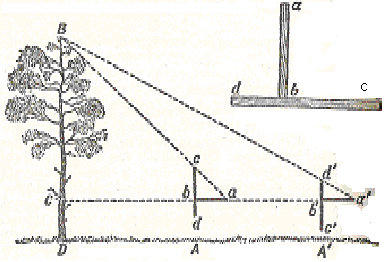

Случается, что почему-либо неудобно подойти вплотную к основанию измеряемого дерева. Можно ли в таком случае определить его высоту?

Вполне возможно. Для этого и придуман остроумный прибор, который, как и предыдущие, легко изготовить самому. Две планки ab и cd скрепляются под прямым углом так, чтобы аb равнялось bc, а bd составляло половину аb. Вот и весь прибор. Чтобы измерить им высоту, держат его в руках, направив планку cd вертикально, и становятся последовательно в двух местах: сначала в точку А, где располагают прибор концом вверх, а затем в точке A', подальше, где прибор держат вверх концом d. (рис. 5) Точка А избирается так, чтобы, глядя из а на конец с, видеть его на одной прямой с верхушкой дерева. Точку же А' отыскивают так, чтобы, глядя из а' на точку d', видеть её совпадающей с В. В отыскании этих двух точек А и А' заключается всё измерение, потому что искомая часть высоты дерева ВС равна расстоянию АА'. Равенство вытекает, как легко сообразить, из того, что аС=ВС, а а'С=2ВС; значит, a'C-aC=BC.

Вы видите, что, пользуясь этим простым прибором, мы измеряем дерево, не подходя к его основанию ближе его высоты. Само собою разумеется, что если подойти к стволу возможно, то достаточно найти только одну из точек – А или А', чтобы узнать его высоту.

Вместо двух планок можно воспользоваться четырьмя булавками, разместив их на дощечке надлежащим образом; в таком виде «прибор» ещё проще.

ГЕОМЕТРИЯ У РЕКИ

Измерение ширины реки

В какие ситуации только не поставит человека жизнь. Никогда не знаешь, что может пригодиться завтра утром! Возможно однажды понадобится даже умение измерять ширину реке. Благо, сделать это можно без специального оборудования и даже не переплывая водную преграду. Вычисляется ширина любой реки по свойствам подобия треугольников из школьного курса геометрии.

Не переплывая реки, измерить её ширину – так же просто для знающего геометрию, как определить высоту дерева, не взбираясь на вершину. Непреступное расстояние измеряют теми же приёмами, какими мы измеряли недоступную высоту. В обоих случаях определение искомого расстояния, легко поддающегося непосредственному измерению.

Из многих способов решения этой задачи рассмотрим несколько наиболее простых.

1)Для первого способа понадобится уже знакомый нам «прибор» с тремя булавками на вершинах треугольника.. Пусть требуется определить ширину АВ реки (рис.6), стоя на том берегу, где точка В, и не перебираясь на противоположный. Став где-нибудь у точки С, держите булавочный прибор близ глаз так, чтобы, смотря одним глазом вдоль двух булавок, вы видели, как обе они покрывают точки В и А.

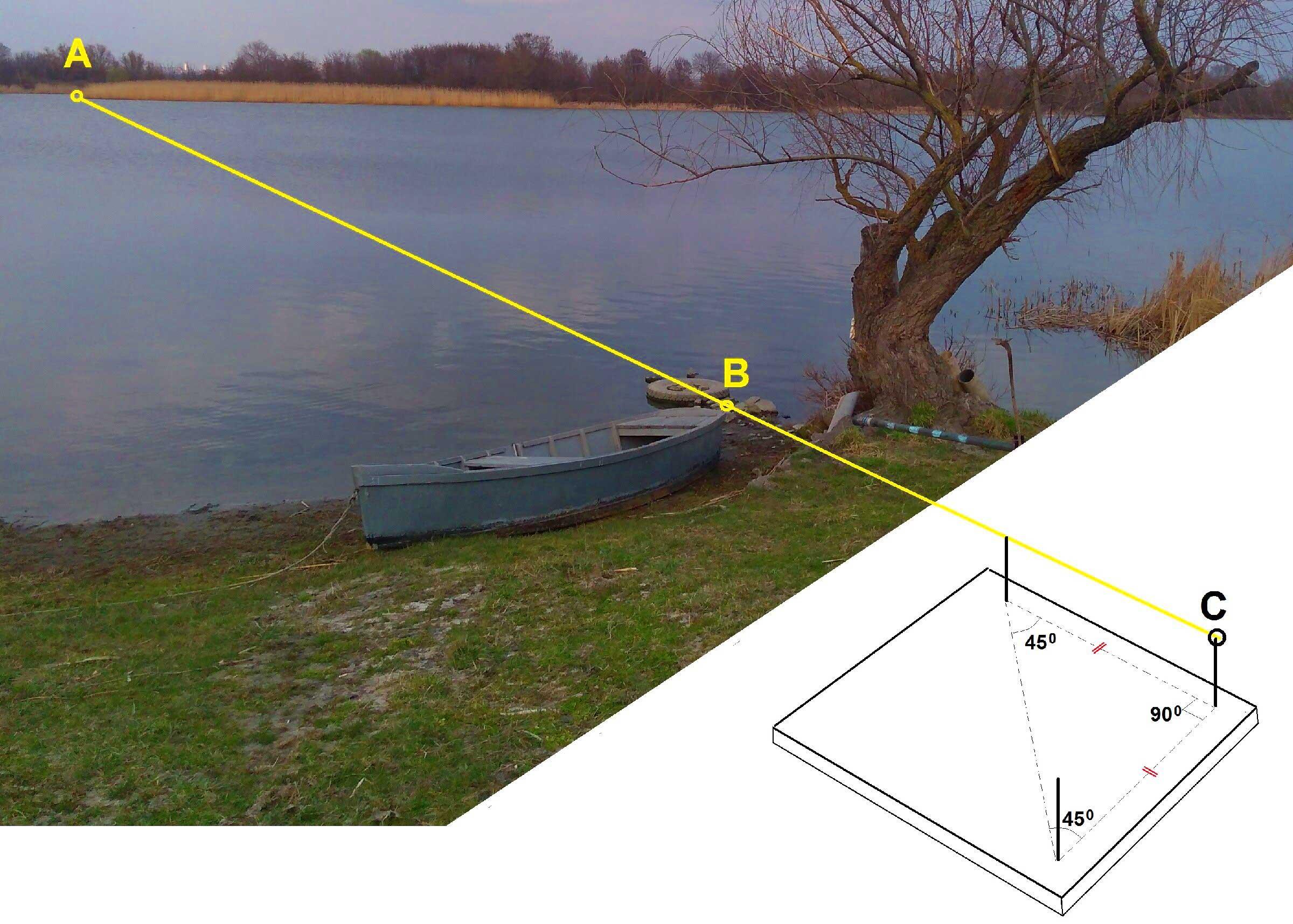рис. 6

Понятно, что, когда это вам удастся, вы будете находиться как раз на продолжении прямой АВ. Теперь, не двигая дощечки прибора, смотрите вдоль других двух булавок и заметьте точку D, покрываемую этими булавками, т.е. лежащую на прямой, перпендикулярной к АС. После этого воткните в точку С веху, покиньте это место и идите с вашим инструментом вдоль прямой СD, пока не найдёте на ней такую точку Е (рис.7), откуда можно одновременно покрыть для глаза булавкой b шест точки С, а булавкой а – точку А.

рис. 7

Это будет значить, что вы отыскали на берегу третью вершину треугольника АСЕ, в котором угол С – прямой, а угол Е равен острому углу булавочного прибора, т.е. ½ прямого. Очевидно, и угол А равен – прямого, т.е. АС=СЕ. Если вы измерите расстояние СЕ хотя бы шагами, вы узнаете расстояние АС, а отняв ВС, которое легко измерить, определите искомую ширину реки.

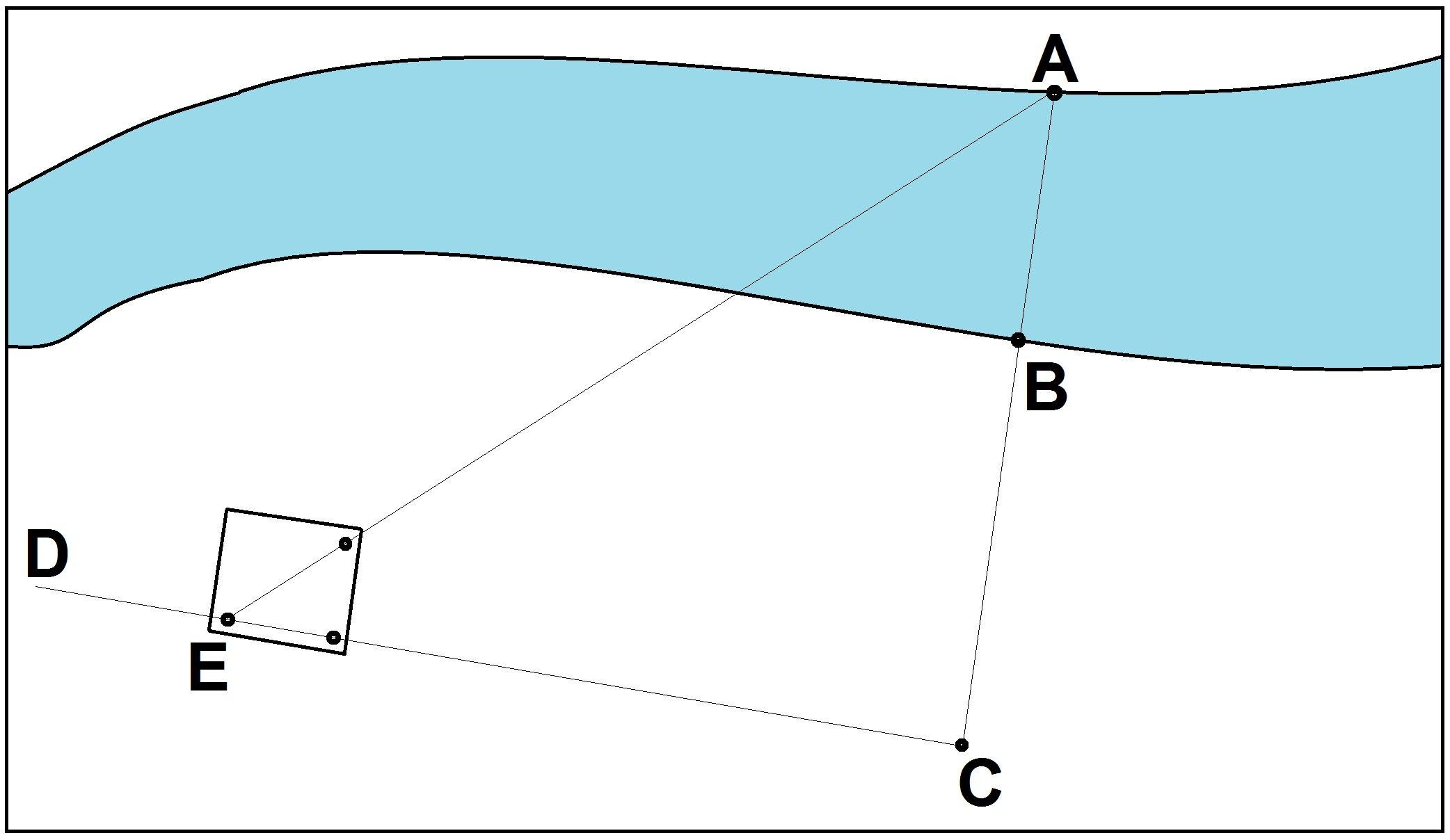рис.8

2) Сначала выбираем две наиболее приметные точки на берегах А и В, после чего ставим колышек в точку С, которая должна лежать с точками А и В на одной прямой линии на любом удалении от берега(рис.6). От колышка делаем 10 шагов к следующей точке О так, чтобы наше движение было перпендикулярно отрезку АС (рис.7). Ставим на месте О еще один колышек.

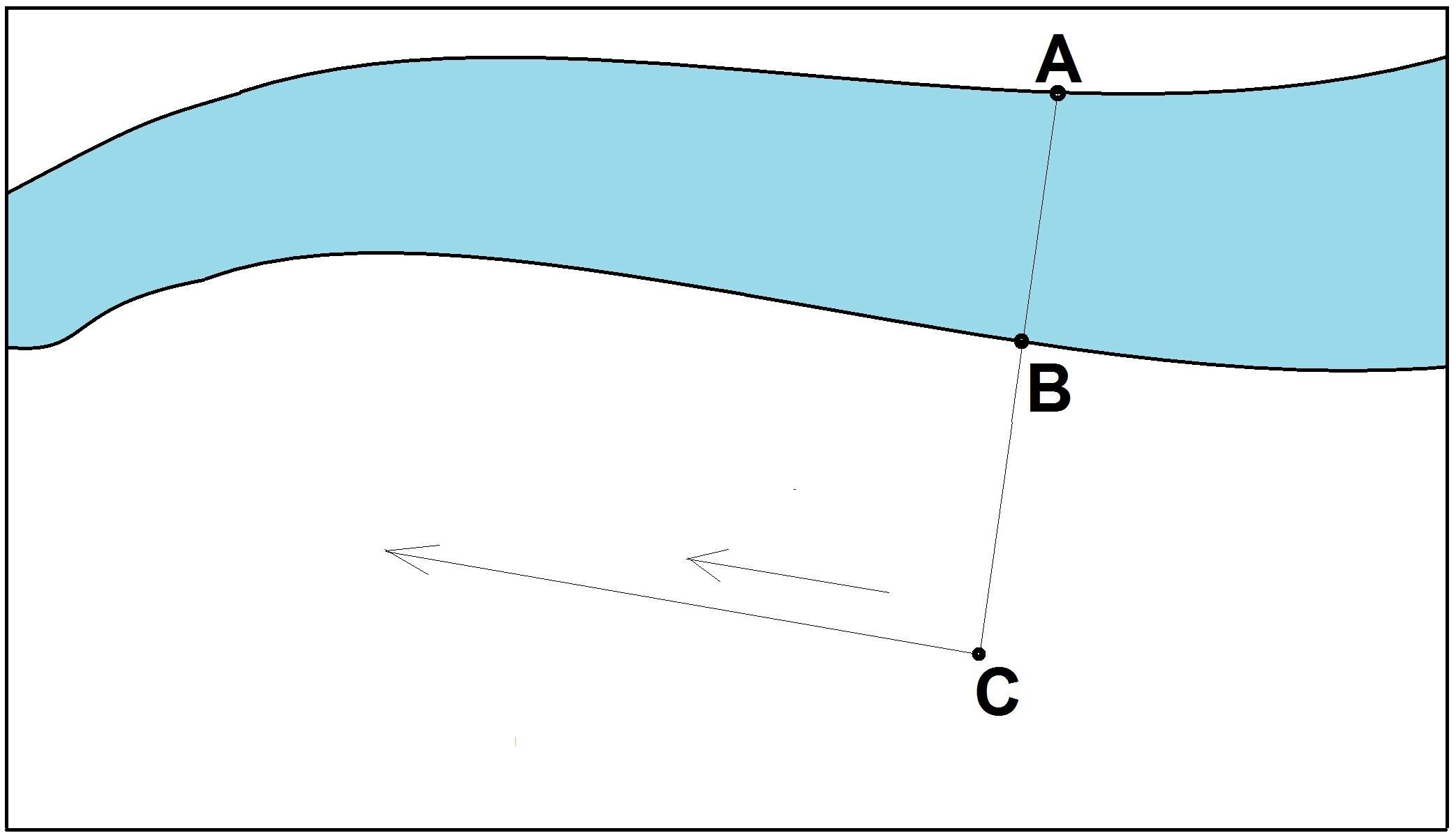рис.6

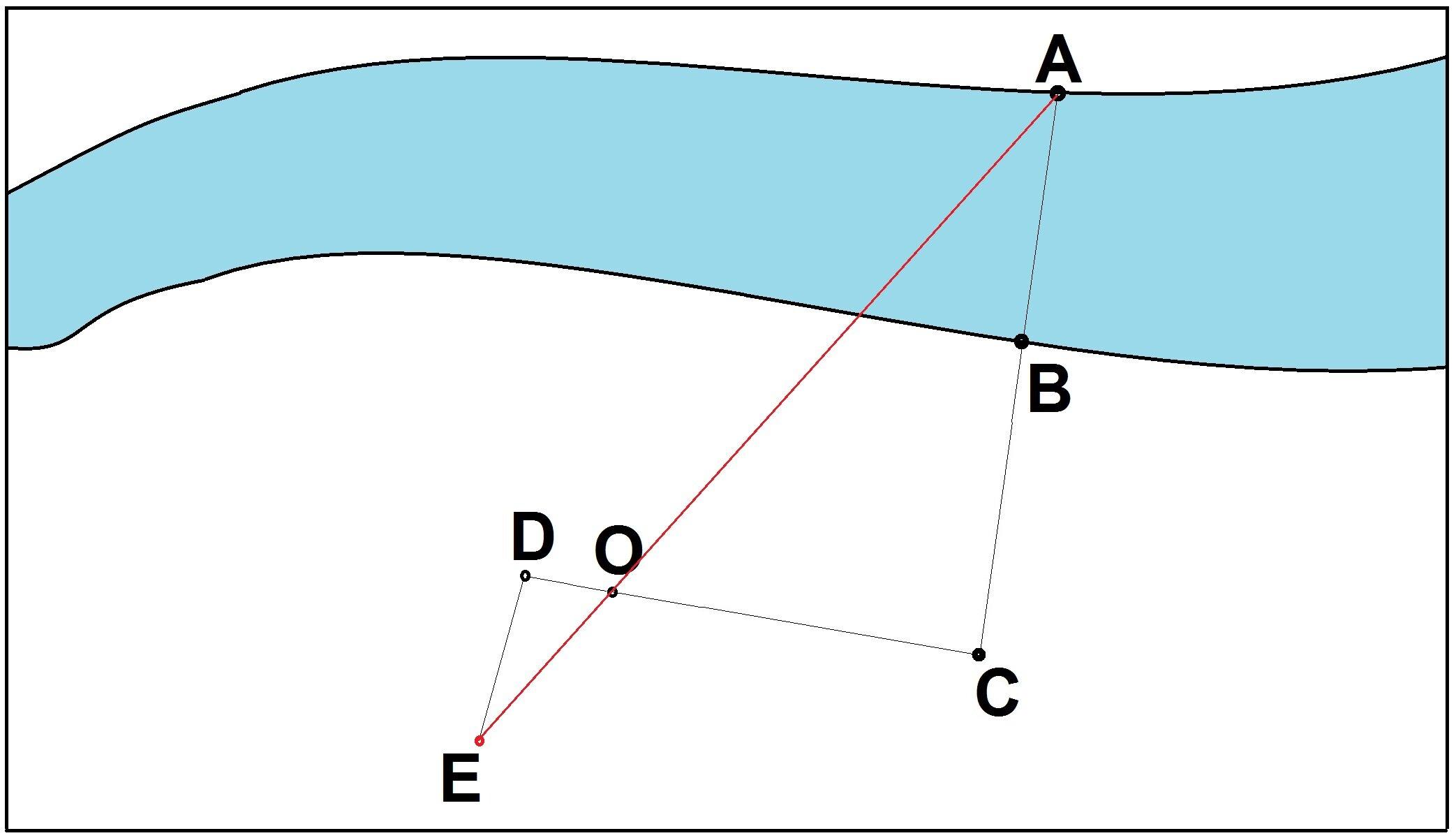рис.7

Продолжаем идти по прямой еще два шага и ставим колышек D, делаем несколько шагов вбок от прямой так, чтобы получить отрезок DЕ под прямым углом относительно отрезка СD. После этого соединяем линией точки Е и А. Если все было сделано правильно, то отрезок пройдет через точку О, и мы получим два подобных треугольника АСО и ОDЕ с соотношением сторон 1 к 5. Таким образом отрезок АС будет равен 5 отрезкам DЕ. А так как расстояние от точки В до точки С мы знаем, то можно вычесть из отрезков ширину реки.Этот способ требует больше места, сем первый; если местность позволяет осуществить оба приёма, полезно проверить один результат другим.

3) Описанный сейчас способ можно видоизменить: отмерить на прямой СF не равные расстояния, а одно в несколько раз меньше другого. Например, (рис.8) отмеряют FE в четыре раза меньше ЕС, а далее поступают по-прежнему: по направлению FG, перпендикулярному к FC, отыскивают точку Н, из которой веха Е кажется покрывающей точку А. Но теперь уже FH не равно АС, а меньше этого расстояния в четыре раза: треугольники АСЕ и HFЕ подобны. Из подобия треугольников следует пропорция

АС:FH=СЕ:ЕF=4:1.

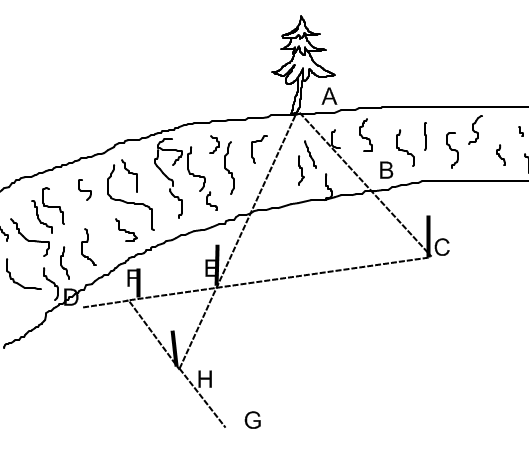рис. 8

Значит, измерив FH и умножив результат на 4, получим расстояние АС, а отняв ВС, узнаем искомую ширину реки.

Этот способ требует, как мы видим, меньше места и потому удобнее для выполнения, чем предыдущий.

4) Четвёртый способ основан на том свойстве прямоугольного треугольника, что если один из его острых углов равен 30', то противолежащий катет составляет половину гипотенузы. Убедиться в правильности этого положения осень легко. Пусть угол В прямоугольного треугольника АВС равен 30'; докажем, что в таком случае АС=1/2АВ. Повернём треугольник АВС вокруг ВС так, чтобы он расположился симметрично своему первоначальному положению (рис.9), образовав фигуру АВD; линия АСD – прямая, потому что оба угла у точки С прямые. В треугольнике АВD угол А=60', угол АВD, как составленный из двух углов по 30', тоже равен 60'. Значит, АD=BD как стороны, лежащие против равных углов. Но АС=1/2AD; следовательно, АС=1/2АВ.

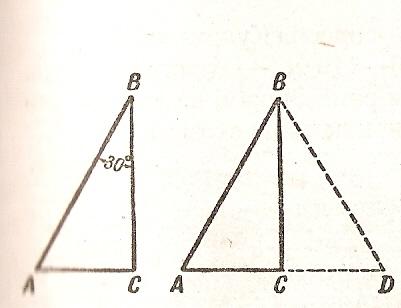
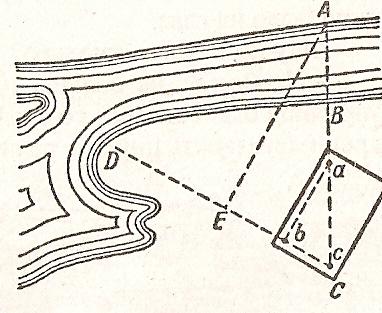
Рис. 9 Рис. 10

Желая воспользоваться этим свойством треугольника, мы должны расположить булавки на дощечке так, чтобы основания их обозначали прямоугольный треугольник, в котором катет вдвое меньше гипотенузы. С этим прибором мы помещаемся в точке С (рис.10) так, чтобы направление АС совпадало с гипотенузой булавочного треугольника. Смотря вдоль короткого катета этого треугольника, намечают направление СD и отыскивают на нём такую точку Е, чтобы направление ЕА было перпендикулярно к СD. Легко сообразить, что расстояние СУ – катет, лежащий против угла 30', - равно половине АС. Значит, измерив СЕ, удвоив это расстояние и отняв ВС, получим искомую ширину АВ реки.

Вот четыре легко выполнимых приёма, при помощи которых всегда возможно, не переправляясь на другой берег, измерить ширину реки со вполне удовлетворительной точностью. Способов, требующих употребления более сложных приборов, мы здесь рассматривать не будем.

Глубина пруда

У древних индусов был обычай задачи и правила предлагать в стихах. Вот одна из таких задач:

ЗАДАЧА

Над озером тихим,

С полфута размером, высился лотоса цвет.

Он рос одиноко. И ветер порывом

Отнёс его в сторону. Нет

Воле цветка над водой,

Нашёл же рыбак его ранней весной

В двух футах от места, где рос.

Итак, предложу я вопрос:

Как озера вода

Здесь глубока?

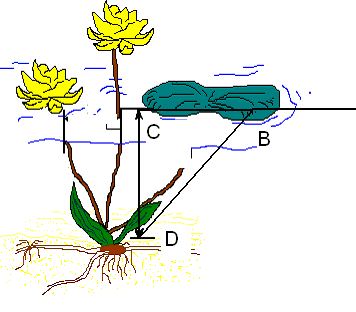рис.11

РЕШЕНИЕ

Обозначим искомую глубину СD пруда через х. (рис. 11). Высота стебля над водой 1/2 фута. Когда ветер отнёс цветок в сторону, он лёг на воду. Значит BD = х + 1/2. Тогда, по теореме Пифагора, имеем:

BD²-х²=ВС², т.е. х²=(х+1/2)²-2², откуда х²=х²+х+1/4-4, х=3(3/4).

Искомая глубина – 3(3/4) фута.

Близ берега реки или неглубокого пруда вы можете отыскать водяное растение, которое доставит вам реальный материал для подобной задачи: без всяких приспособлений, не замочив даже рук, определить глубину водоёма в этом месте.

Заключение

Геометрия возникла на основе практической деятельности, поэтому важно знать как при помощи геометрии измерить некоторые величины.

Целью работы служит рассмотреть применение геометрии на практике.

Рассмотренные примеры в работе позволяют измерить высоту дерева несколькими способами, не залезая на него (по длине тени, при помощи простого булавочного прибора, при помощи записной книжки), измерить ширину реки и глубину пруда.

Данная работа важна тем, что наглядно показывает, что геометрия – это не просто школьный предмет, а наука, находящая применение в жизни.

Практическое применение работы состоит в том, чтобы использовать знания и умения в решении задач по геометрии, расширении кругозора учащихся.

Список литературы

1. Атанасян Л.С., Бутузов А.Ф., Кадомцев С.В. и др. Геометрия 10-11 кл. – М.: Просвещение, 2003г. – 206с.

1. Брохгауз Ф.Б. Иллюстрированный энциклопедический словарь.-М.: Эксмо, 2006-960с.

1. Перельман Я.И. Занимательная алгебра, занимательная геометрия.-М. : АСТ, 2007-474с.

14