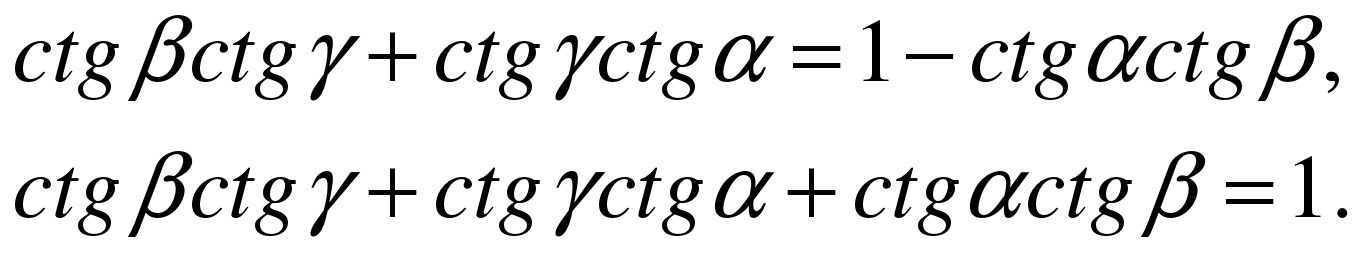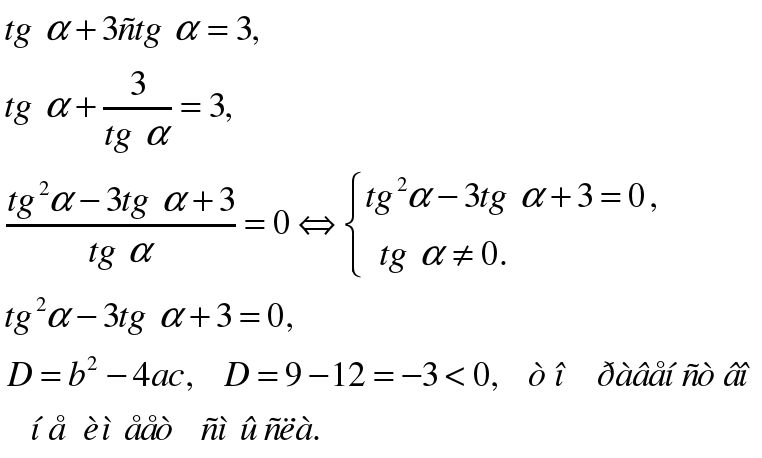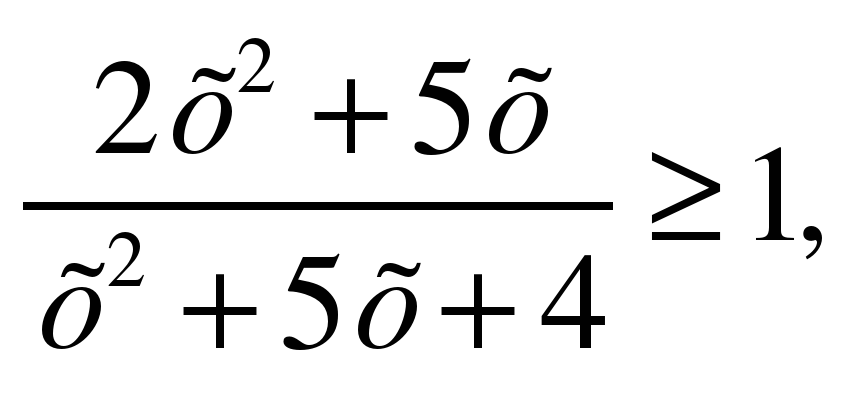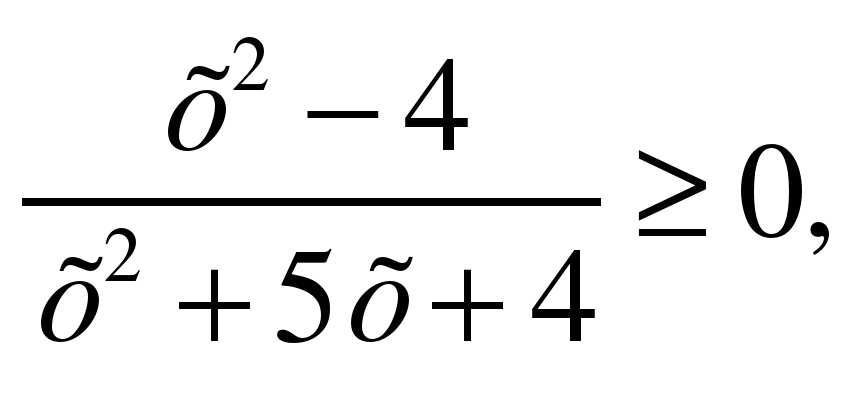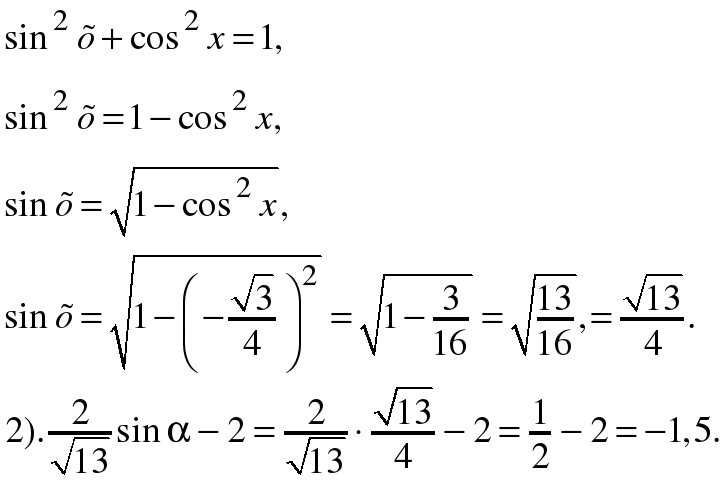Алгебра и начала анализа – 10 класс
Тема урока: Применение основных тригонометрических формул
к преобразованию выражений.
Цели урока: 1. Повторить основные тригонометрические формулы и проверить
умения и навыки учащихся применять их: для упрощения
выражений; для доказательства тождеств; для предварительных
упрощений и последующих вычислений.
2. Развивать логическое и творческое мышление, целеустремленность
в достижении цели, умение точно и сжато выражать свои мысли.
3. Способствовать воспитанию трудолюбия и дисциплины, создать
атмосферу заинтересованности каждого ученика в работе класса.
Тип урока: урок закрепления знаний, умений, навыков.
Оборудование: учебник, тетрадь, ручка, карандаш, линейка, индивидуальные
оценочные листы.
Наглядность: справочный материал, карточки.
Ход урока.
I. Организационный момент.
Приветствие учащихся.
Проверить готовность к уроку.
Сообщить тему урока, сформулировать цели и план урока.
Если поручить двум людям, один из которых – математик, выполнение любой незнакомой работы, то результат всегда будет следующим: математик сделает ее лучше.
Г. Штейнгауз
II. Проверка домашнего задания.
На оценку «3» у доски № 11(а, б), № 25 (а, б), № 27 (а, б).
На оценку «4» и «5»
Задания по уровням. По карточкам (три человека).
|
Карточка № 1. Сравнить, что больше: sin 10 или sin 11?
|
Решение.
Рассмотрим разность sin 10 – sin 11 = 2sin0,5cos10,5. Поскольку угол (0,5) находится в первой четверти, то sin 0,5 положителен. Остается выяснить, где расположен угол 10,5. Поскольку 3π  [3π; 3π + ½ π], то cos10,5 меньше 0. Следовательно, sin11 меньше sin10.
[3π; 3π + ½ π], то cos10,5 меньше 0. Следовательно, sin11 меньше sin10.
Ответ: sin11 sin10.
|
Карточка № 2. Доказать, что если α, β, γ – углы треугольника, то ctgαctgβ + ctgβctgγ + ctgγctgα=1.
|
Решение.
Так как α, β, γ – углы треугольника, то α + β + γ = π, то
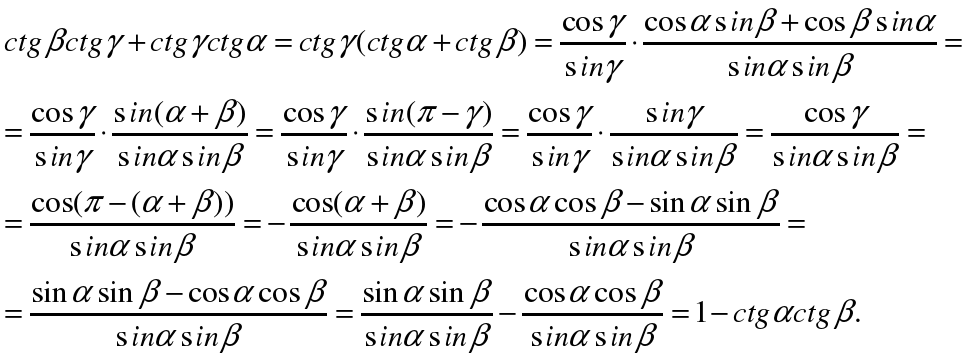 2. Значит,
2. Значит,
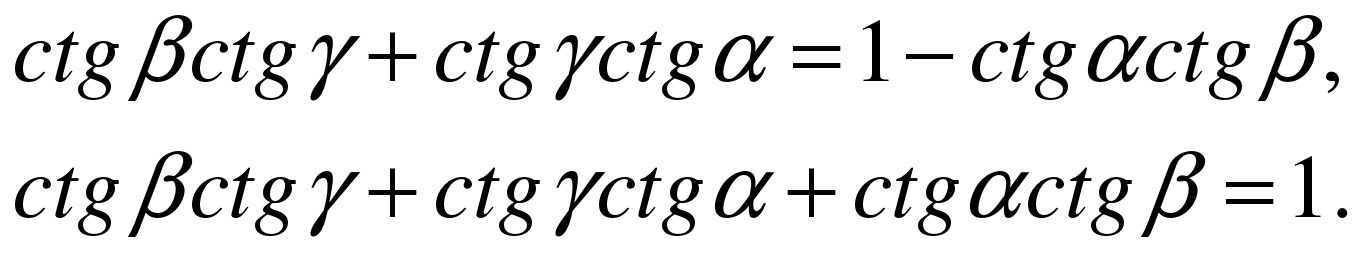
Ответ: 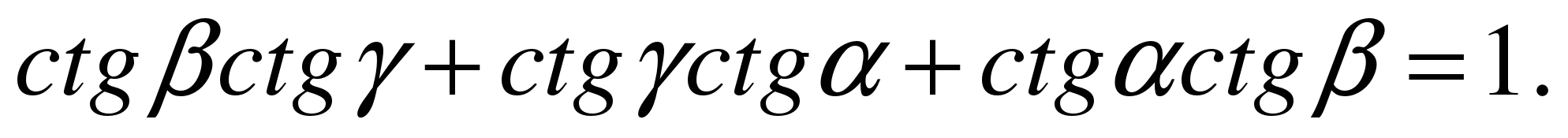
|
Карточка № 3. Можно ли вычислить 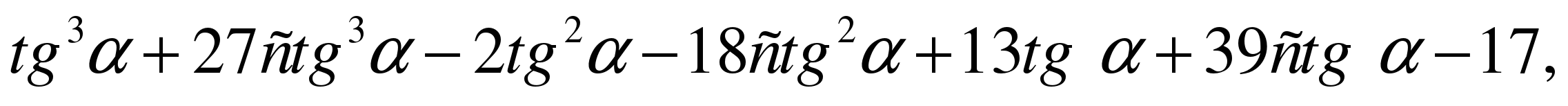
если 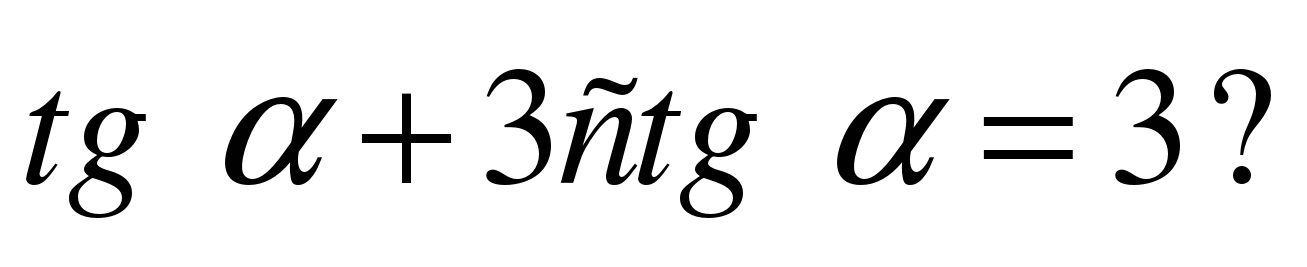
|
Решение.
Рассмотрим равенство:
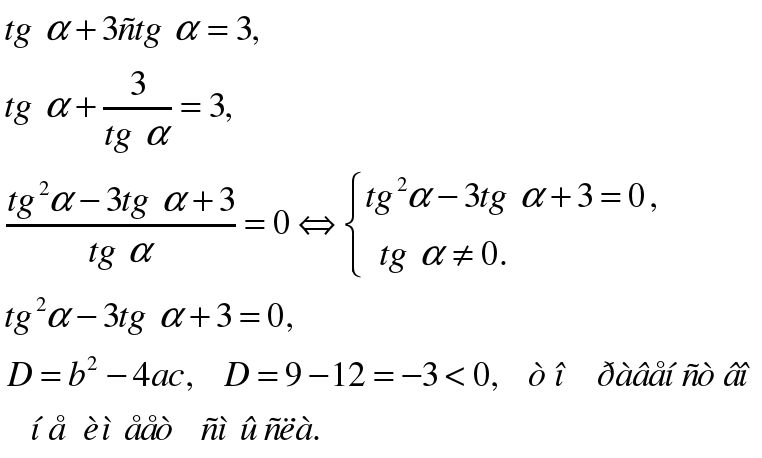
Значит, значение выражения 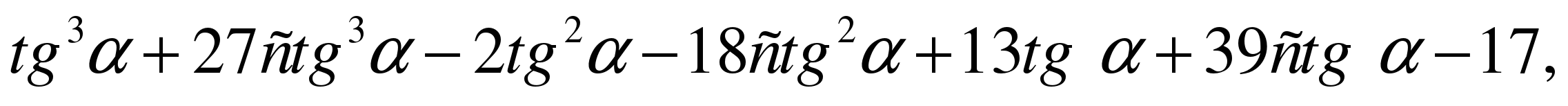
вычислить нельзя.
Ответ: нельзя.
III. Устная работа.
1.Понятие числовой окружности. (Окружность единичного радиуса с центром в точке О (0; 0) с выбранным началом отсчета А (1;0) и установленным положительным и отрицательным направлением движения по ней называется числовой окружностью).
2. Определение синуса числа х. (Ордината точки, лежащей на числовой окружности, называется синусом числа х и обозначается sin x).
3. Определение косинуса числа х.
4. Определение тангенса числа х.
5. Определение котангенса числа х.
6. Назовите основные тригонометрические тождества.
7. Формулы сложения.
8.Формулы суммы и разности синусов (косинусов).
9. Формулы двойного аргумента.
10. Формулы половинного аргумента.
IV. Физкультминутка. Для глаз.
Не поворачивая головы, делать движения глазами: вправо – влево; вверх – вниз. Не поворачивая головы, делать движения глазами: «восьмерка». На вытянутой руке держать ручку или карандаш, зафиксировать взгляд на карандаше, приближая и отодвигая его.
V. Повторение. Решение алгебраических неравенств (метод интервалов).
1. Решить неравенство:
а) 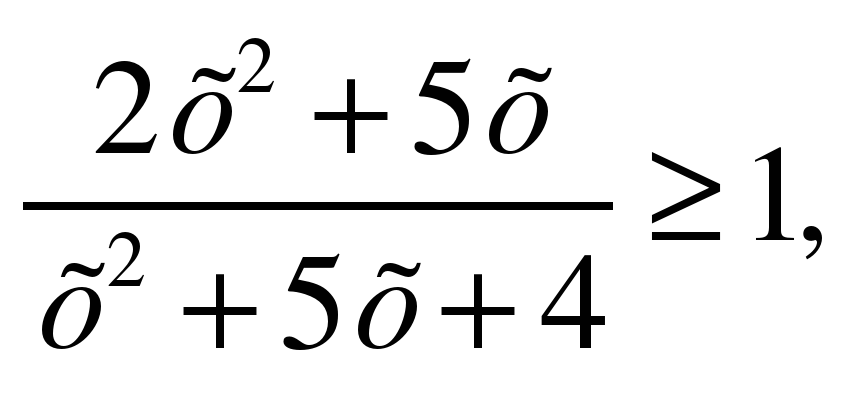
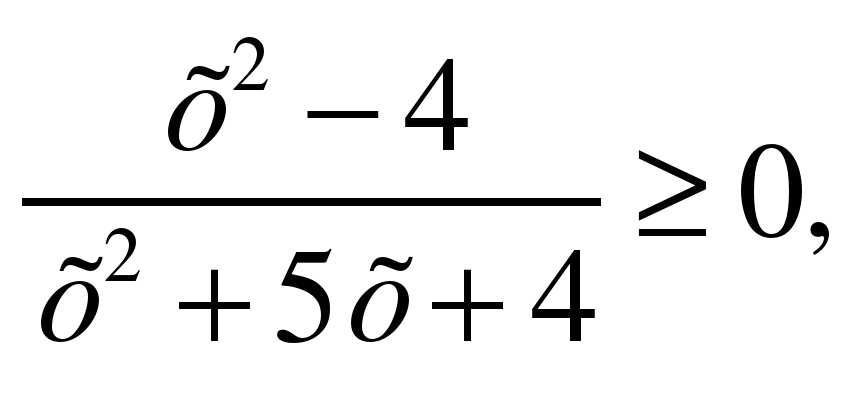
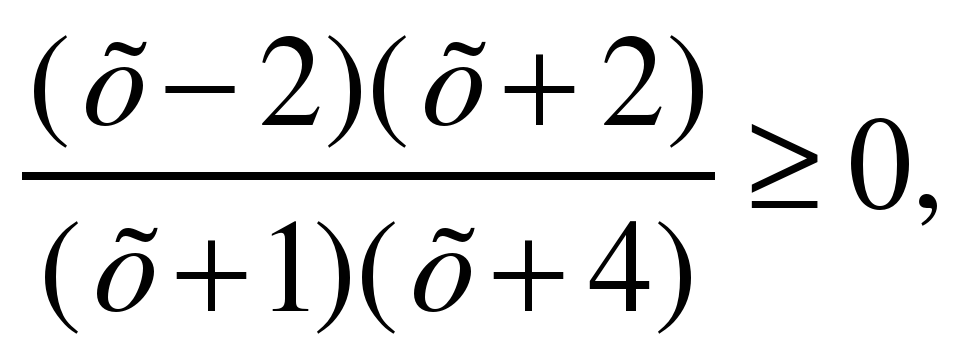
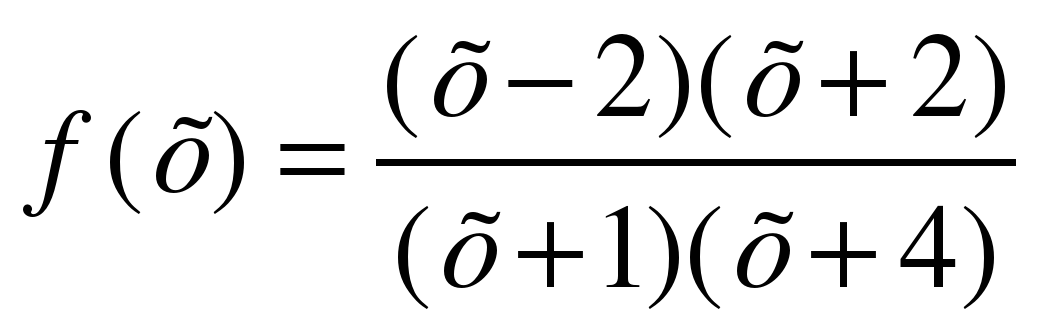
f(х) = 0, если х = – 2, х = 2, причем х ≠ – 1, х ≠ – 4,
Ответ: (– ∞; – 4) U [– 2; – 1) U [2; +∞).
б) 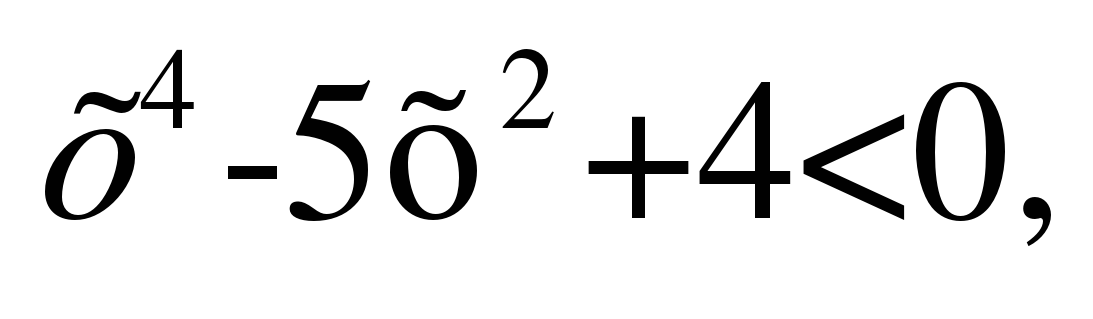
( х – 1)( х + 1)( х – 2)( х + 2)
Ответ: (– 2; – 1)U(1; 2).
VI. Работа на уроке в группах. Задания по уровням. Задание № 1.
1.Заполните таблицу.
| α | 0 | π/6 | π/4 | π/3 | π/2 | π | 3/2π | 2π |
| sin α |
|
|
|
|
|
|
|
|
| cos α |
|
|
|
|
|
|
|
|
| tg α |
|
|
|
|
|
|
|
|
| ctg α |
|
|
|
|
|
|
|
|
2.Раставить знаки синуса, косинуса, тангенса и котангенса.
| Четверти | sinα | cosα | tgα | ctgα |
| I |
|
|
|
|
| II |
|
|
|
|
| III |
|
|
|
|
| VI |
|
|
|
|
3.Заполните таблицу.
Заполняет весь класс.
|
| π/2-α | π/2+α | π-α | π+α | 3/2π-α | 3/2π+α | 2π-α |
| sin α |
|
|
|
|
|
|
|
| cos α |
|
|
|
|
|
|
|
| tg α |
|
|
|
|
|
|
|
| ctg α |
|
|
|
|
|
|
|
|
Задание № 2. Найдите значение выражения 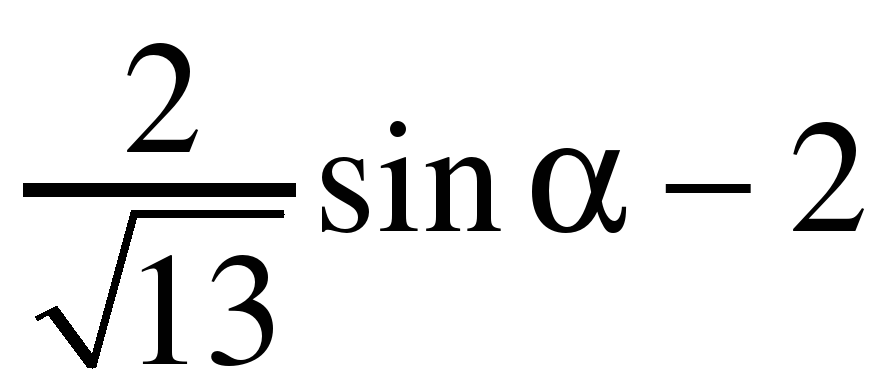 , если , если 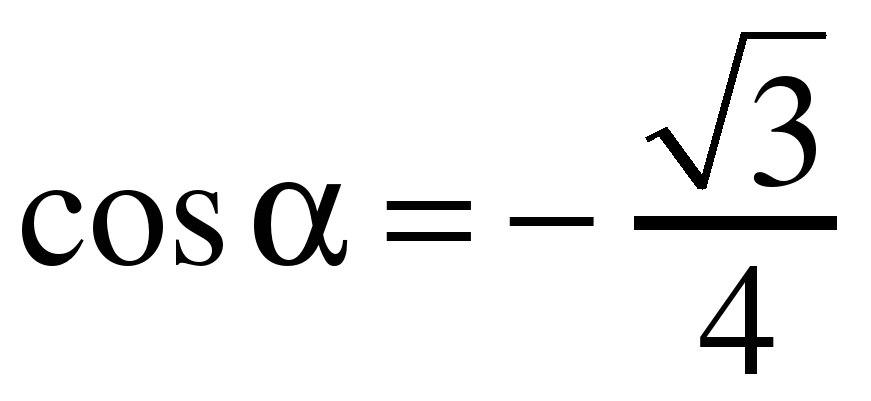 , , 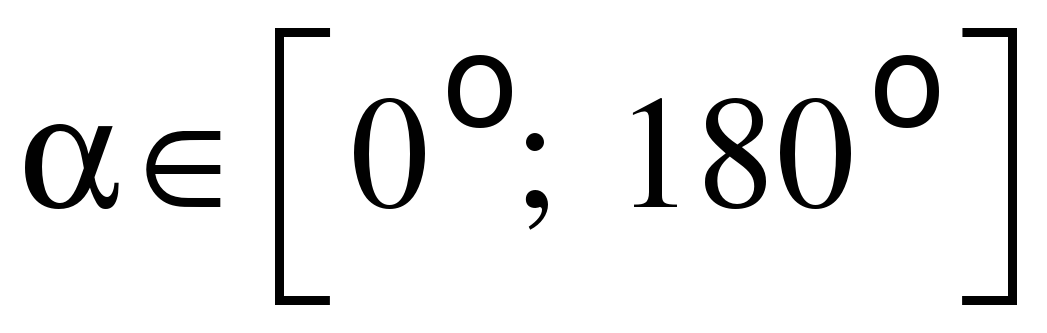 . .
|
Решение. 1). Так как cos х II четверти, значит, sin х 0, тогда
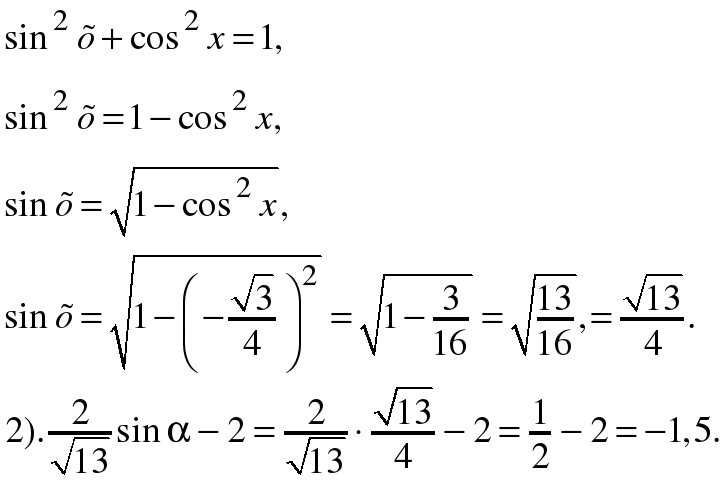
Ответ: – 1,5.
|
Задание № 3. Решите уравнение 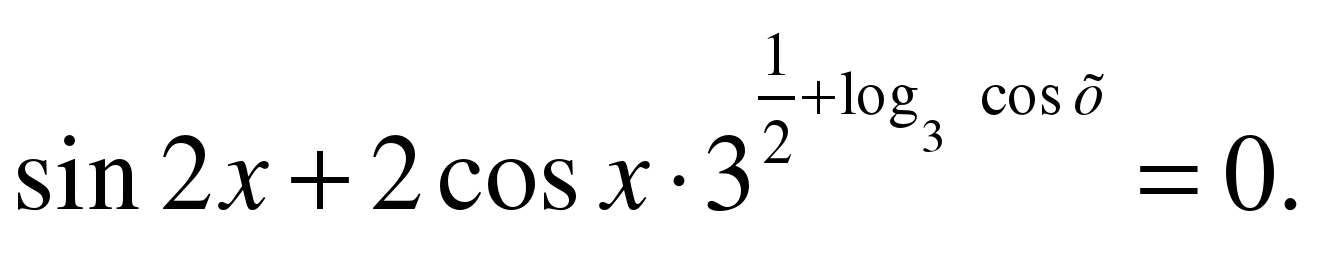
|
Решение. 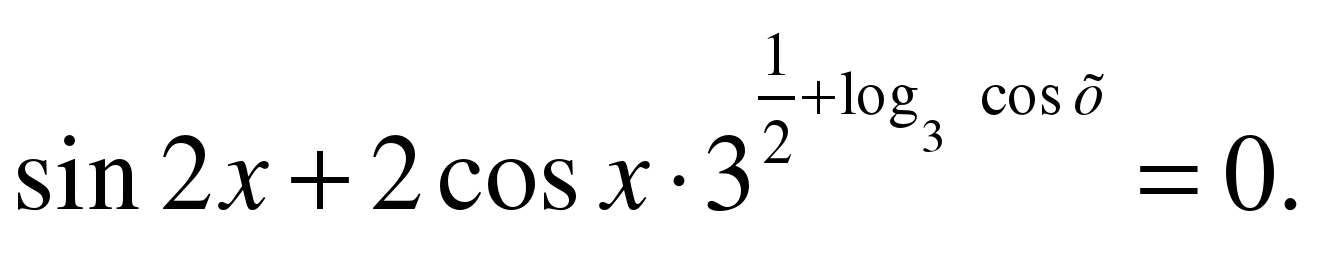
ОДЗ: cos х 0,
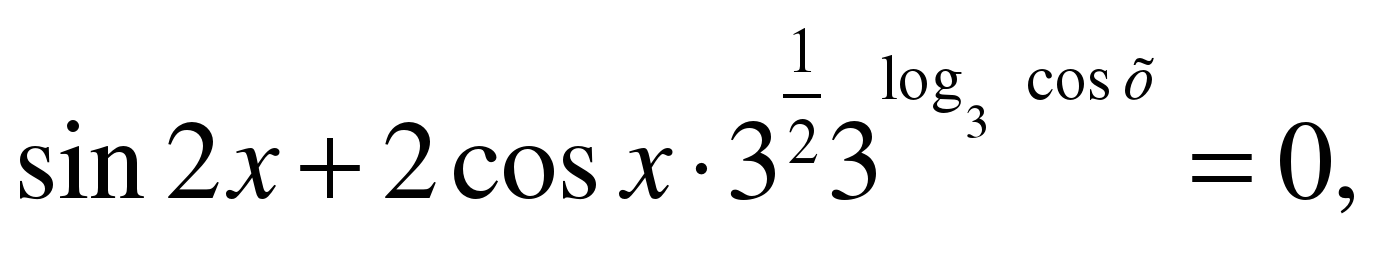
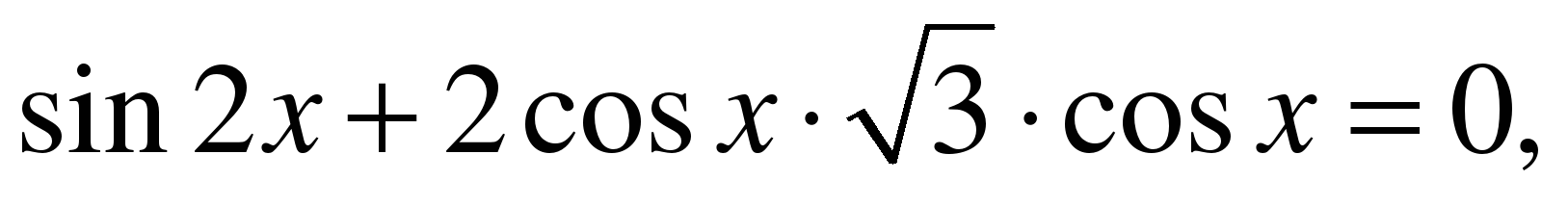
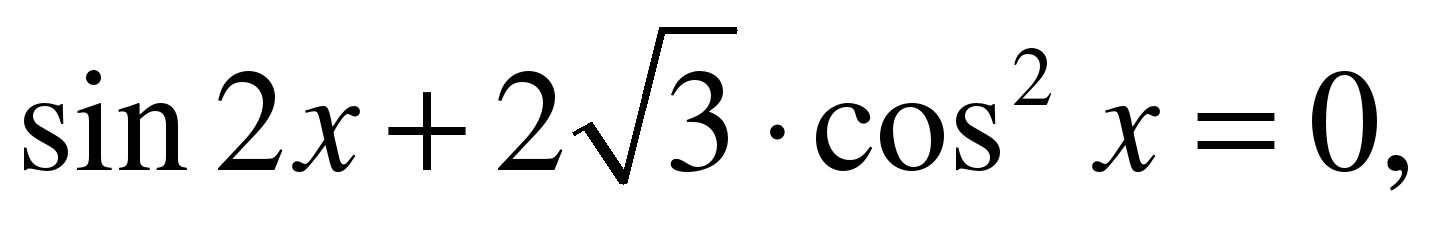
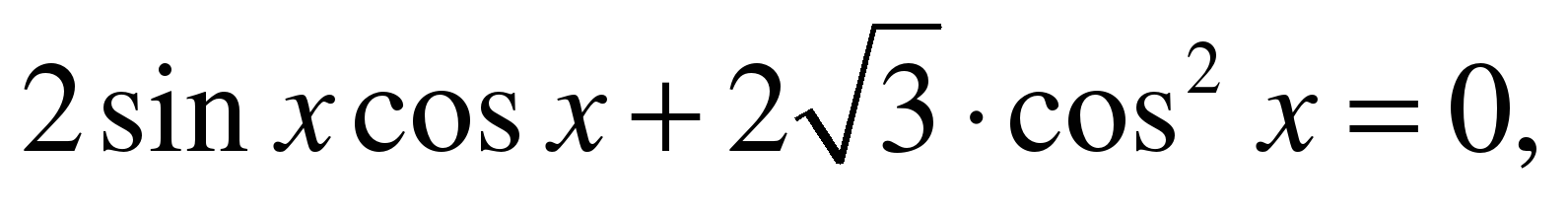
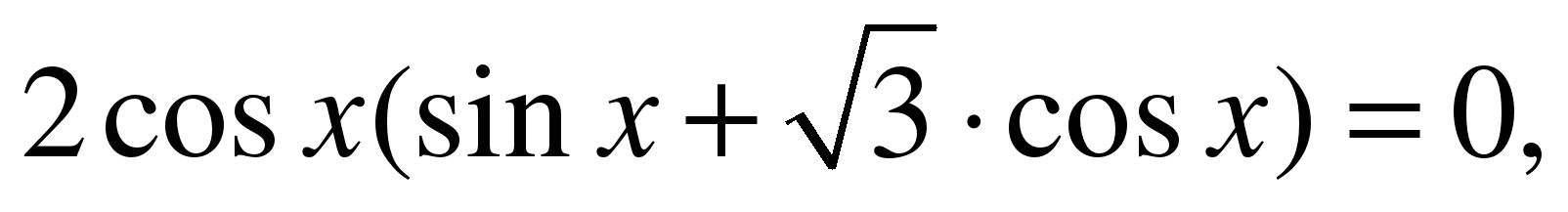
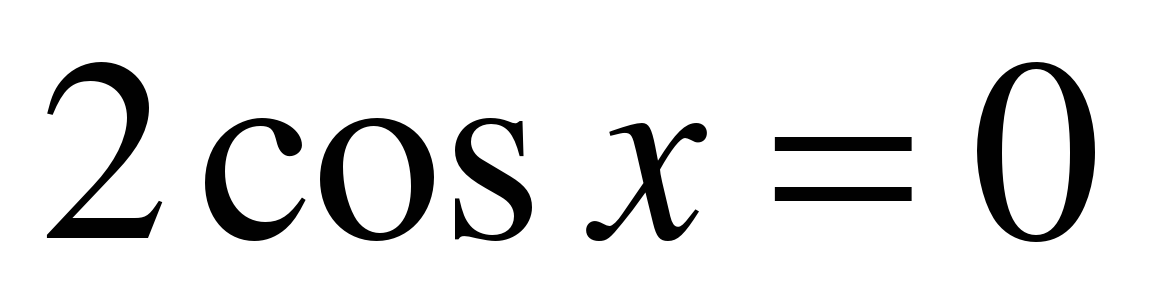 или
или
или
1). С учетом ОДЗ уравнение не имеет решений.
2).
С учетом ОДЗ
Ответ: .
VII. Диктант на сообразительность. Я считаю, что
sin 30° = ½.
sin²α + cos²α = 1
tg 45° = √3
В первой четверти тангенс положительный.
Полный угол поворота равен π.
Сумма углов треугольника равна π.
Ордината точки, лежащей на числовой
окружности, называется синусом числа х.
Абсцисса точки, лежащей на числовой окружности, называется тангенсом числа х.
sin (– α ) = sin α.
cos (– α ) = cos α.
| sin α| ≤ 1
а² – в² = (а-в)(а+в).
13.
75² =5625.
sin2α = 2sinαcosα .
cos2α = 2cosαsinα.
sin( π + α ) = sin α.
VIII. Самостоятельная работа.
| Вариант 1
|
| 1 | Вычислите , если .
|
| 2 | Решите неравенство . |
| Вариант 2
|
| 1 | Вычислите , если .
|
| 2 | Решите неравенство . |
| Вариант 3
|
| 1 | Найдите значение выражения , если
|
| 2 | Найдите значение выражения , если . |
| Вариант 4
|
| 1 | Вычислите: , при .
|
| 2 | Вычислите , если и . |
IX. Итоги урока.
Выставление оценок.
Что нового узнали на уроке?
Чему научились?
X. Домашнее задание.
Обязательная часть (на «3») п. 1, № 11(в, г), № 25 (в, г), № 27 (в, г).
Дополнительная часть (на «4» и «5»).
Доказать тождество:
| Доказать тождество: Решение. |
Оценочный лист ученика
|
Фамилия, имя
|
|
Этапы урока
|
Задания |
Количество баллов |
|
1
|
Домашнее задание |
|
|
2 |
Устная работа
|
|
|
3 |
Работа по карточкам
|
|
|
4 |
Работа по таблицам
|
|
|
5 |
Повторение
|
|
|
6 | Диктант на сообразительность
|
|
|
7 |
Работа на уроке
|
|
|
8 |
Самостоятельная работа (вторая оценка) |
|
|
Количество баллов |
|
Оценка |






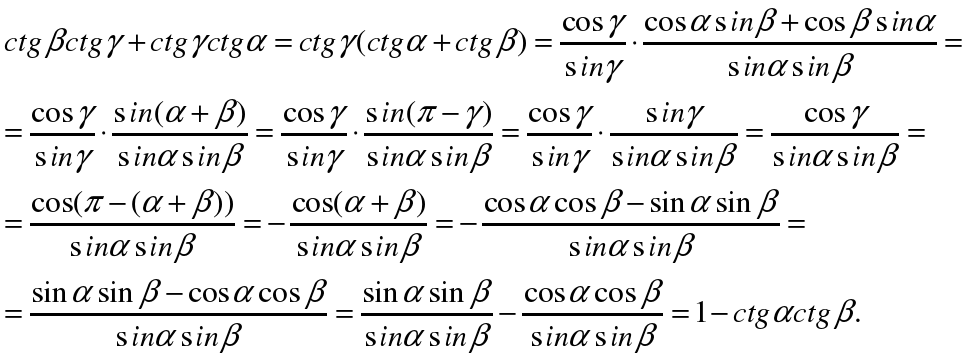 2. Значит,
2. Значит,