Конспект урока по алгебре и начала анализа, 10 класс
Тема: «Преобразование основных тригонометрических формул к преобразованию выражений»
Цель: формирование умений в применении основных тригонометрических формул к преобразованию выражений.
Задачи:
-Закреплять умения в применении основных тригонометрических формул к преобразованию выражений.
-Воспитывать умение слушать друг друга, лидерские качества, навыки коллективной работы.
-Развивать у учащихся внимательность, логическое мышление, память;
-Развивать интерес к предмету
Ход урока
1.Организационный момент:
2. Проверка домашнего задания.
3. Устная работа
Какому выражению соответствует значение  ?
?
а) sin30°;
б) cos ;
;
в) tg
Выбрать верное равенство
а) sinα = ;
;
б) cosα =  -2;
-2;
в) sinα = -3,7.
Какой из углов является углом II четверти?
а)  ;
;
б) –145°;
в) 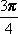
В каких четвертях sinα и cosα имеют разные знаки?
а) II и IV;
б) I и III;
в) I и IV.
Каким выражением можно заменить  ?
?
а) cosα;
б) sinα;
в) - sinα.
Ответ: 1б; 2б; 3в; 4а; 1б.
Пример 1. Вычислить  .
.
Решение. Имеем  . Воспользуемся формулой сложения двух аргументов и получим
. Воспользуемся формулой сложения двух аргументов и получим
 .
.
Ответ:  .
.
Пример 2. Известно, что  . Найти
. Найти  .
.
Решение. Из формулы, связывающей одинаковые аргументы тригонометрических функций получаем  . Подставив заданное значение синуса, получим
. Подставив заданное значение синуса, получим
 .
.
Значит  либо
либо  . По условию,
. По условию,  , т.е. аргумент принадлежит III четверти. В III четверти косинус отрицателен, значит
, т.е. аргумент принадлежит III четверти. В III четверти косинус отрицателен, значит
 .
.
Ответ: -0,8.
Пример 3. Упростить выражение  .
.
Решение.
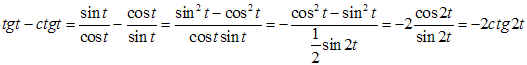 .
.
4. Математический диктант. | Вариант 1 | Вариант 2 |
| tg (3π/2+α)= | cos(π/2+α)= |
| 1+tg2α = | 1+ctg2α= |
| cos (π-α)= | sin(π+α)= |
| sin(α-β)= | tgα·ctgα= |
| sin2α + cos2α= | cos(α+β)= |
| sin2α= | сos2α= |
| 1- sin2α = | 1-cos2α= |
| sinα - sinβ= | сosα - cosβ= |
Все учащиеся работают в тетрадях. Два ученика выполняют работу на закрытых досках.
Учащиеся проверяют работы одноклассников, работающих на обратной стороне доски, и одновременно свои работы.
5. Применение тригонометрических формул к преобразованию выражений. 1. Вычислить.
Работа выполняется письменно в тетради с дальнейшей проверкой на слайдах компьютерной презентации.
| №/№ | Задание | Ответ |
| I. У доски с объяснением | 


| 


|
| II. Самостоятельно с устной проверкой | 
|

|
| III. Самостоятельно с проверкой у доски |
| 0,5х – 1 = 0; х = 2
2х – 4 = 0; х = 2 |
2. Найти значение выражения.
Учащиеся выполняют работу по вариантам, самостоятельно, для проверки меняются тетрадями с соседом.
Первые несколько человек сдают работу на проверку консультантам, которые ставят в тетрадь плюсы по количеству выполненных заданий.
Задания - на слайдах презентации.
Ответы в презентации во время проверки: 1вар-134; 2вар-324.
3. Найти по заданному значению тригонометрической функции остальные функции.
Учащиеся выполняют заданиясамостоятельно письменно в тетрадях, проверяют их устно на доске.
4. Упростить тригонометрические выражения:
а) задания для I и II групп:
| I группа | Ответ | IIгруппа | Ответ |
| 
| 
| 
| 
|
| 
| 
| 
| 
|
| 
| 
| 
| 
|
б) третья группа выполняет задания по карточкам
| Задание | Ответ |
| Доказать тождество:
|
|
| Упростить:
 | 
|
| Упростить выражение:
| 
|
5.Обучающая самостоятельная работа под копирку (самопроверка)
Вариант 1 Вариант 2
|  1. 1.
| 
|
|  2. 2.
| 
|
|  3. 3.
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| Найдите значение выражения:  . . | Найдите значение выражения:  |
Ответы
|
| Вариант 1 | Вариант 2 |
| 1 | 5 | 40 |
| 2 | -14 | -2 |
| 3 | -47 | 4 |
| 4 | -5 | -23 |
| 5 | 14 | -42 |
| 6 | 19 | 22 |
| 7 | 7 | 16 |
| 8 | -51 | -30 |
| 9 | 6 | -24 |
| 10 | -9 | 4 |
6. Резерв. Учащиеся, выполнившие задания, сдают в конце урока тетради на проверку.
1. Упростите выражения:
2) cos2α – (ctg2α +1) sin2α.=
3)
4)
2. Докажите тождество:
1) (tg α+ctg α)2– (tg α–ctg α)2= 4
Тождество доказано.
2) (1+tg α)2+(1-tg α)2= ;
;
Тождество доказано.
3) (2+ sin β)(2- sin β)+(2+ cos β)(2– cos β)=7
Тождество доказано.
7. Домашнее задание. 1 группа: №№7.6, 7.8, 7.12, 9.8.
2 группа: №№ 7.8, 7.13, 9.10, 9.12.
3 группа: №№ 7.16, 7.19, 7.20, 9.11, 9.14.
8. Рефлексия. Подведение итогов урока. Выставление оценок за работу на уроке.







 .
.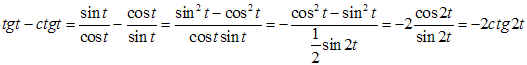 .
.









