11 класс
Тема: «Применение производной к решению задач».
Тип урока: обобщение и повторение знаний и умений
Цель урока:добиться усвоения учащимися систематических, осознанных сведений о понятии производной, её геометрическом и физическом смысле.
Задачи урока
Образовательные: повторить основные формулы и правила дифференцирования, применение производной к исследованию функции, нахождению наибольшего и наименьшего значения функции, геометрический смысл производной; сформировать умение комплексного применения знаний, умений, навыков и их перенос в новые условия; проверить знания, умения, навыки учащихся по данной теме, продолжить подготовку учащихся к ЕГЭ по математике.
Развивающие: содействовать развитию мыслительных операций: анализ, синтез, обобщение; формированию умений самооценки и взаимооценки.
Воспитательные: содействовать формированию творческой деятельности учащихся.
Оборудование:
План урока:
1. Организационное начало урока,целеполагание.
Актуализация знаний
Групповая работа
Проверка выполненных заданий.
Итог занятия
Домашнее задание.
Ход урока:
1. Организация начала урока.
Учителем сообщается тема урока применение производной к решению задач, на уроке повторим основные формулы и правила дифференцирования, применение производной к исследованию функции, нахождению наибольшего и наименьшего значения функции, геометрический смысл производной
Актуализация субъективного опыта учащихся, их знаний.
Задача: повторить и закрепить навыки вычисления производной,
применение производной к решению задач;
проверить сформированность грамотной математической речи.
Форма подачи заданий: мультимедийный проектор.
| 
слайд 1 |  слайд 2 слайд 2
|
Устно
| Задача по физике 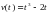 1. Материальная точка движется попрямой так, что ее скорость в момент времени t равна 1. Материальная точка движется попрямой так, что ее скорость в момент времени t равна
Найдите ускорение точки в момент времени t = 3.
Слайд 4 | Задача по химии. 3. Пусть количество вещества, вступившего в химическую реакцию задается зависимостью: р(t) = t2/2 + 3t –3 (моль) Найти скорость химической реакции через 3 секунды. Слайд 5 |
| Задча по экономоке. Объем продукции V цеха в течение дня зависит от времени по закону V(t) = -5/3t3+15/2t2+50t+70. Вычислите производительность труда П(t).
Слай 6 | 4. Найдите угловой коэффициент , касательной, проведенной к графику функции f(x) = 7x –5 lnx в его точке с абсциссой х0 =1.
Слайд 7 |
| 5. Найдите тангенс угла наклона касательной, проведенной к графику функции
f(x) = x5 – 5x2 – 3 в его точке с абсциссой х0 = - 1.
Слайд 8 | 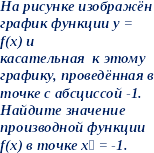
Слайд 9 |
|  Слайд 10 |
 Слайд 11 |
|
 Слайд 12 |
 Слайд 13 |
3. Применение знаний и умений.
Форма: групповая письменная
Задача: содействовать формированию активной творческой деятельности,
развивать мотивацию учащихся, сформировать умение
комплексного применения знаний, умений, навыков и их перенос в
новые условия; проверить знания, умения, навыки учащихся по
данной теме.
Форма подачи заданий: карточки
Задания для 1 группы
1. В какие моменты времени ток в цепи равен нулю, если количество электричества, протекающего через проводник, задается формулой: а) q = t + k / t .
2.Координата материальной точки изменяется с течением времени по закону х(t) = 3t 2 - 7t + 6. Найдите скорость точки в момент времени t = 6.
Задания для 2 группы
B8.Прямая 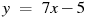 параллельна касательной к графику функции
параллельна касательной к графику функции 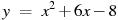 . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
Задания для 3 группы
B14.Найдите наименьшее значение функции 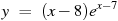 на отрезке
на отрезке 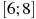 .
.
4. Защита учащимися выполненных работ.
Форма: фронтальная
Задача: проверить знания, умения, навыки учащихся по данной теме.
Учащиеся оформляют решения на доске и поясняют ход выполнения заданий. Каждая группа, выслушивая защиту других.
5. Подведение итогов урока.
Задача: определить уровень достижения целей урока и меру участия каждого учащегося в занятии, оценка работы школьников.
6.Домашнее задание.
На рисунке 1 изображён график функции 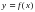 и касательная к этому графику, проведённая в точке с абсциссой
и касательная к этому графику, проведённая в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции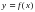 в точке
в точке 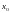 .
.
На рисунке 2 изображён график функции 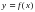 и касательная к этому графику, проведённая в точке с абсциссой
и касательная к этому графику, проведённая в точке с абсциссой 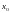 . Найдите значение производной функции
. Найдите значение производной функции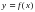 в точке
в точке  .
.
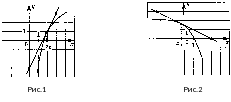
На рисунке 3 изображён график функции 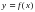 и касательная к этому графику, проведённая в точке с абсциссой
и касательная к этому графику, проведённая в точке с абсциссой 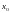 . Найдите значение производной функции
. Найдите значение производной функции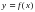 в точке
в точке 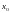 .
.
Функция  определена на отрезке[-4;4]. На рисунке 4 изображён график её производной
определена на отрезке[-4;4]. На рисунке 4 изображён график её производной . Найдите точку минимума этой функции.
. Найдите точку минимума этой функции.
Функция  определена на отрезке [-4;4]. На рисунке 5 изображён график её производной
определена на отрезке [-4;4]. На рисунке 5 изображён график её производной . Найдите точку максимума этой функции.
. Найдите точку максимума этой функции.

Найдите наименьшее значение функции на отрезке
на отрезке
[-4,5;0] .
Найдите точку максимума функции  .
.
Угловой коэффициент касательной к графику функции равен значению функции в точке касания. Найдите абсциссу точки касания.
равен значению функции в точке касания. Найдите абсциссу точки касания.






 слайд 2
слайд 2
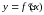
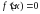
 слайд 3
слайд 3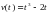 1. Материальная точка движется попрямой так, что ее скорость в момент времени t равна
1. Материальная точка движется попрямой так, что ее скорость в момент времени t равна 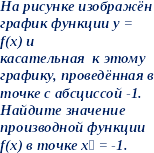



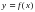 и касательная к этому графику, проведённая в точке с абсциссой
и касательная к этому графику, проведённая в точке с абсциссой 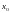 . Найдите значение производной функции
. Найдите значение производной функции










