Принцип Дирихле

П ринцип д ирихле

Дирихле Петер Густав Лежен

Немецкий математик, внёсший существенный вклад в математический анализ, теорию функций и теорию чисел. Член Берлинской и многих других академий наук, в том числе Петербургской.

Биография

Дирихле родился в вестфальском городе Дюрене в семье почтмейстера. В 12 лет Дирихле начал учиться в гимназии в Бонне, спустя два года в иезуитской гимназии в Кёльне, где в числе прочих преподавателей его учил Георг Ом. С 1822 по 1827 г. жил в качестве домашнего учителя в Париже, где вращался в кругу Фурье. Биография

В 1827г. устраивается на должность приватдоцента университета Бреслау (Вроцлав).

В 1829 г. он перебирается в Берлин, где проработал непрерывно 26 лет, сначала как доцент. Затем с 1831 г. как экстраординарный профессор. С 1839 г. как ординарный профессор Берлинского университета.

В 1855 г. Дирихле становится в качестве преемника Гаусса профессором высшей математики в Гёттингенском университете.

Принцип дирихле

Это утверждение сформулированное Густавом Дирихле в 1834, устанавливающие связь между объектами и контейнерами при выполнении определённых условий. В английском и некоторых других языках утверждение известно как «принцип голубей и ящиков», когда объектами являются голуби, а контейнерами — ящики. После немецкого математика совершенствованием принципа никто из математиков не занимался, поскольку Лежён-Дирихле всё точно исследовал.

n, то хотя бы в одной клетке сидят по крайней мере два зайца». На первый взгляд даже непонятно, почему это совершенно очевидное замечание является весьма эффективным методом решения задач. Дело в том, что в каждой конкретной задаче нелегко бывает понять, что же здесь «зайцы» и «клетки» и почему зайцев больше, чем клеток. Выбор зайцев и клеток часто неочевиден; далеко не всегда по виду задачи можно определить, что следует воспользоваться принципом Дирихле. А главное, этот метод дает неконструктивное доказательство (мы, естественно, не можем сказать, в какой именно клетке сидят два зайца, а знаем только, что такая клетка есть), а попытка дать конструктивное доказательство, т. е. доказательство путем явного построения или указания требуемого объекта, может привести к гораздо большим трудностям. " width="640"

Принцип дирихле

Самая популярная формулировка принципа Дирихле такова: «Если в n клетках сидит m зайцев, причем m n, то хотя бы в одной клетке сидят по крайней мере два зайца». На первый взгляд даже непонятно, почему это совершенно очевидное замечание является весьма эффективным методом решения задач. Дело в том, что в каждой конкретной задаче нелегко бывает понять, что же здесь «зайцы» и «клетки» и почему зайцев больше, чем клеток. Выбор зайцев и клеток часто неочевиден; далеко не всегда по виду задачи можно определить, что следует воспользоваться принципом Дирихле. А главное, этот метод дает неконструктивное доказательство (мы, естественно, не можем сказать, в какой именно клетке сидят два зайца, а знаем только, что такая клетка есть), а попытка дать конструктивное доказательство, т. е. доказательство путем явного построения или указания требуемого объекта, может привести к гораздо большим трудностям.

n, то хотя бы в одной клетке сидят, по крайней мере, два зайца. " width="640"

• Если в n клетках сидит m зайцев, причем m n, то хотя бы в одной клетке сидят, по крайней мере, два зайца.

Если в n клетках сидит m голубей, причем m

12, то, по принципу Дирихле, найдется, как минимум, одна «клетка», в которой будет сидеть, по крайней мере, 2 «зайца». Ответ: Найдется месяц, в котором будут отмечать дни рождения не менее 2 учеников класса. Задача 1. " width="640"

Задача 1

• В классе 15 учеников. Докажите, что найдутся как минимум 2 ученика, отмечающих дни рождения в один месяц.
• Решение: Пусть 15 учеников будут «зайцы». Тогда «клетками» будут месяцы года, их 12. Так как 1512, то, по принципу Дирихле, найдется, как минимум, одна «клетка», в которой будет сидеть, по крайней мере, 2 «зайца».
• Ответ: Найдется месяц, в котором будут отмечать дни рождения не менее 2 учеников класса. Задача 1.

Задача 2

• В ковре размером 3х3 метра Коля проделал 8 дырок. Докажите, что из него можно вырезать коврик размером 1х1 метр, не содержащий внутри себя дырок.
• Решение: Разрежем ковер на 9 ковриков размерами 1х1 метр, Так как ковриков - «клеток» - 9, а дырок - «голубей» - 8.
• Ответ: Найдется коврик без дырок внутри.

Задача 3

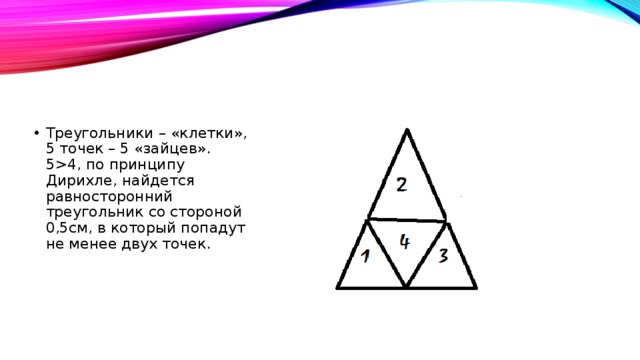
Внутри равностороннего треугольника со стороной 1см расположено 5 точек. Докажите, что расстояние между некоторыми двумя из них меньше 0,5см.

Решение: Можно получить 4 «клетки», разбив равносторонний треугольник с помощью проведения отрезков, соединяющих середину сторон. Тогда получим 4 равносторонних треугольника со сторонами по 0,5 см, которые и будут у нас «клетками».

4, по принципу Дирихле, найдется равносторонний треугольник со стороной 0,5см, в который попадут не менее двух точек. " width="640"

• Треугольники – «клетки», 5 точек – 5 «зайцев». 54, по принципу Дирихле, найдется равносторонний треугольник со стороной 0,5см, в который попадут не менее двух точек.

Вывод

Таким образом, применяя данный метод, надо: Определить, что удобно в задаче принять за «клетки», а что за «зайцев». Получить «клетки»; чаще всего «клеток» меньше (больше), чем «зайцев» на одну (или более). Принцип Дирихле важен, интересен, полезен. Его можно применять в повседневной жизни, что развивает логическое мышление. Многие олимпиадные задачи решаются, используя это специальный метод. Он дает возможность обобщать.

С пасибо за внимание

Проект выполнила

Ученица 7 Класса Б

Гимназии имени А.Л.Кекина

Курбанова Нигина