ОГБПОУ «НОВГОРОДСКИЙ АГРОТЕХНИЧЕСКИЙ ТЕХНИКУМ»
ИНСТРУКЦИОННАЯ КАРТА НА ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКОЙ РАБОТЫ № 5 ПО ДИСЦИПЛИНЕ
ИНФОРМАТИКА.
ТЕМА: «Принципы обработки информации при помощи компьютера. Арифметические и логические основы работы компьютера».
НАИМЕНОВАНИЕ РАБОТЫ: “ Основные логические операции. Таблицы истинности логических выражений.”.
| Наименование объектов контроля и оценки | Основные показатели оценки результата |
| Владение способами представления, хранения и обработки данных на компьютере | Выполнение согласно инструкционным картам и методическим рекомендациям.
|
НОРМА ВРЕМЕНИ: 6 часов.
ОСНАЩЕНИЕ РАБОЧЕГО МЕСТА: ПК, инструкционная карта, калькулятор, тетрадь для ПЗ.
ПРАВИЛА ПО ТЕХНИКЕ БЕЗОПАСНОСТИ согласно инструкции.
ЛИТЕРАТУРА:
Цветкова М.С., Хлобыстова И.Ю. Информатика. Учебник для СПО. М.: Академия. 2017 г. – 352с.
Поляков К.Ю. и др. Информатика в 2-х ч. 10 кл. Учебник. М.: БИНОМ. 2013 г. – 344с. (электронный ресурс)
Теоретическая часть.
1. Таблицы истинности для основных логических операций.
1) Логическое умножение (конъюнкция):
| А | В | S = А*В |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2) Логическое сложение (дизъюнкция):
| А | В | S = А + В |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание (инверсия):
Пример 1. Построить таблицу истинности для логического выражения (AVB) & (A V B)
Решение:
| А | В | AVB | AVB | (AVB) & (A V B) |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
Столбцы 1 и 2 всегда заполняем аналогично разобранному примеру.
Столбцы 3 и 4 заполняем, исходя из таблиц истинности логической операции Дизъюнкция (логическое сложение).
Столбец 5 заполняем, используя данные столбцов 3 и 4, а также таблицей истинности логической операции Конъюнкция (логическое умножение).
Вывод: Логическое выражение (AVB) & (A V B) истинно во всех случаях, кроме случая, когда А=0 и В=0.
Пример 2. Доказать, что логические выражения 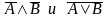 равносильны.
равносильны.
Решение: Построим таблицы истинности для каждого из выражений.
| А | В | 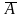
| 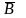
| 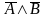
|
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
Для заполнения столбца 3 воспользуемся данными столбца 1 и таблицей истинности для логического отрицания.
Для заполнения столбца 4 воспользуемся данными столбца 2 и таблицей истинности для логического отрицания.
Для заполнения столбца 5 воспользуемся данными столбцов 3 и 4, а также таблицей истинности для логической операции Конъюнкция (логическое умножение).
Аналогично заполняем вторую таблицу истинности.
| А | В | A V B | 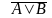
|
| 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 |
Мы видим, что последние столбцы в двух таблицах истинности одинаковые, значит выражения 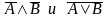 равносильны.
равносильны.
2. Основные законы логики:
| Закон тождества | А=А |
| Закон противоречия | 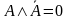
|
| Закон исключения третьего | 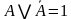
|
| Закон двойного отрицания | 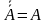
|
| Законы де Моргана | 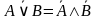
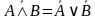
|
| Закон коммутативности | 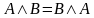

|
| Закон ассоциативности | 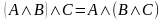
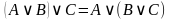
|
| Закон дистрибутивности | 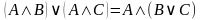
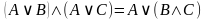
|
Пример. Упростить логическое выражение: 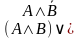 )
)
Решение: Воспользуемся законом дистрибутивности и вынесем за скобки А: 
По закону исключенного третьего 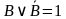 . Следовательно:
. Следовательно: 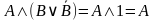
Практическая часть.
Задание 1 Построить таблицу истинности для логического выражения: 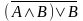
Построить таблицу истинности логического выражения A&(BV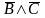 B&C)
B&C)
Построить таблицу истинности для логического выражения: 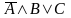
Задание 2 Доказать, что логические выражения 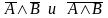 равносильны
равносильны
Доказать, что логические выражения  и А & В равносильны
и А & В равносильны
Задание 3.
Упростить логическое выражение: 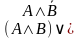 )
)
Упростить логическое выражение: 
Упростить логическое выражение: 
Задание 4.
Вычислить: 2610 &418 → N10
Вычислить: 4710 V 388 → N10
Вычислить:2910 V 3116 → N10
Задание 5. Используя таблицы истинности, решить логическую задачу:
Три ученика, Симонов Саша, Кузин Коля и Вишнёв Ваня, играли во дворе школы в футбол и разбили мячом окно. На вопрос кто разбил окно были получены следующие ответы.
Ваня сказал: “Это я разбил окно, Коля окно не разбивал”.
Коля сказал: “Это сделал не я и не Саша”.
Саша сказал: “Это сделал не я и не Ваня”.
Но дежурная сидела и всё видела. Она сказала, что только один ученик говорит правду, но не назвала его фамилии. Кто из учеников разбил стекло?
Фигуранты дела: Симонов Саша, Кузин Коля и Вишнёв Ваня.
Допрос: на вопрос “Кто разбил окно?” были получены следующие ответы:
Ваня сказал: “Это я разбил окно, Коля окно не разбивал”.
Коля сказал: “Это сделал не я и не Саша”.
Саша сказал: “Это сделал не я и не Ваня”.
Но дежурная сидела и всё видела. Она сказала, что только один ученик говорит правду, но не назвала его фамилии.
Задание 6. Используя таблицы истинности, решить логическую задачу:
В вымогательстве подозреваются Брагин, Кургин и Лиходеев. Каждый их них дол следующие показания:
Брагин: “Я не участвовал в вымогательстве. Это делал Лиходеев”.
Лиходеев: “Я не виноват, но и Кургин тут ни причём”.
Кургин: “Лиходеев не виновен. Вымогательство совершал Брагин”.
Следствием точно установлено, что вымогали двое, кроме того, подозреваемые путались в показаниях и каждый из них не дал полностью правдивых показаний. Кто же совершал вымогательства?
Задание 6. Используя правила преобразования логических выражений, решить логическую задачу:
В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайней мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики.
Задания для самостоятельной работы:
Вариант 1 Вычислить:
3510 &418 → N10
Составить таблицу истинности для логического выражения:
(A&B)&(
Доказать, используя таблицы истинности,
что логические выражения равносильны (или неравносильны).

= A&B
Вариант 2 Вычислить:
3710 V 408 → N10
Составить таблицу истинности для логического выражения:
(A  B)&(
B)&(
Доказать, используя таблицы истинности,
что логические выражения равносильны (или неравносильны).

= A&B
Критерии оценки за самостоятельную работу
Каждое задание оценивается в один балл.
«отлично» - 3 балла;
«хорошо» 2 балла;
«удовлетворительно» - 1 балла;
«неудовлетворительно» - 0 балла и менее.







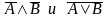 равносильны.
равносильны.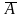
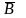
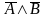
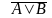
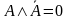
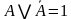
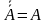
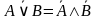
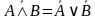
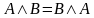

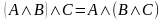
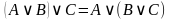
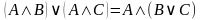
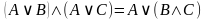
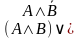 )
)
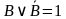 . Следовательно:
. Следовательно: 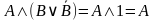
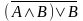
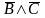 B&C)
B&C)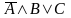
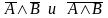 равносильны
равносильны









