Просмотр содержимого документа
«Призма. Параллелепипед. Куб»
Призма. Параллелепипед. Куб.
ПРИЗМА
ПРИЗМОЙ называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки многоугольников.
Многоугольники называются ОСНОВАНИЯ призмы, отрезки – БОКОВЫЕ РЕБРА
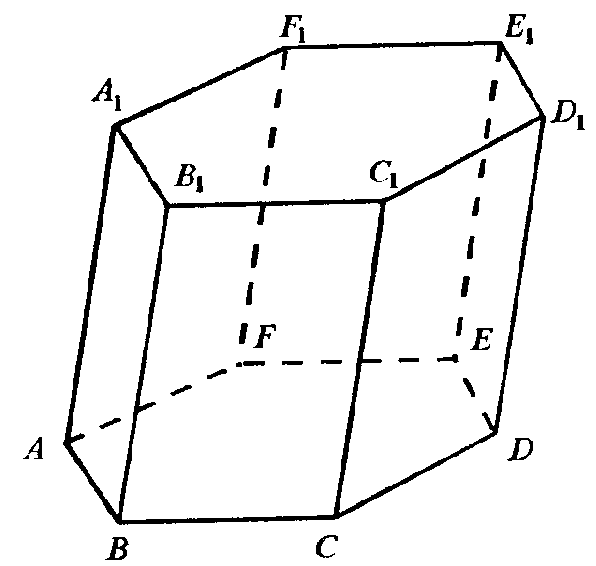
ABCDEFA1B1C1D1E1F1 – призма
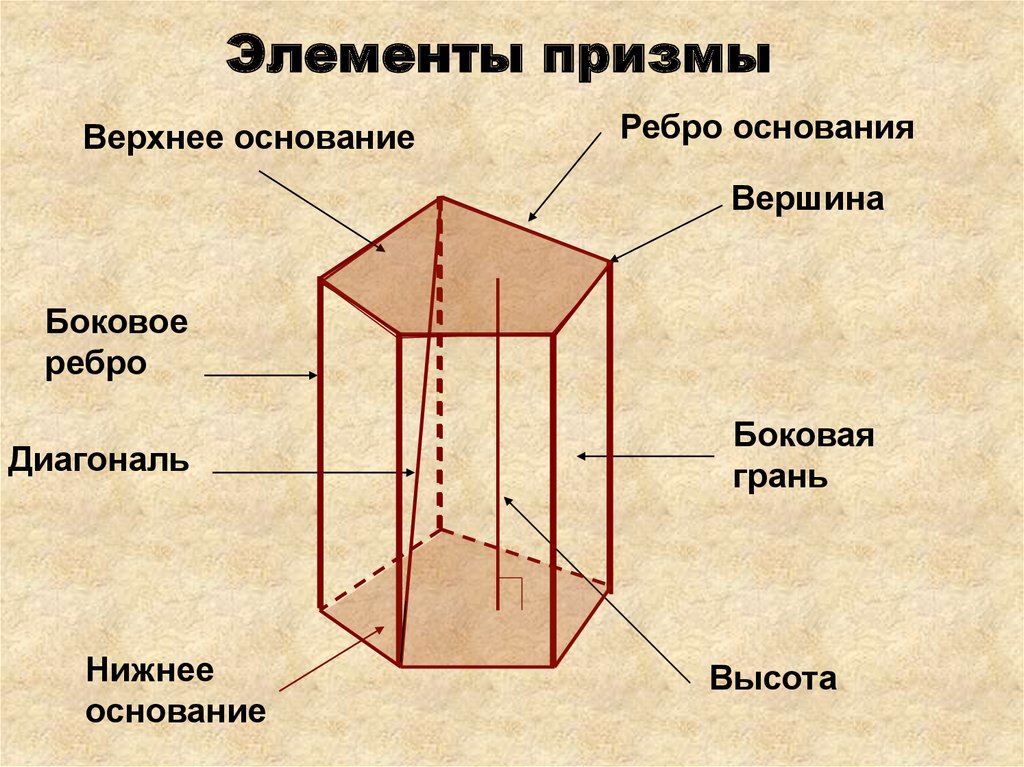
Свойства призмы:
Основания призмы равны.
У призмы основания лежат в параллельных плоскостях.
У призмы боковые ребра параллельны и равны.
Виды призм:
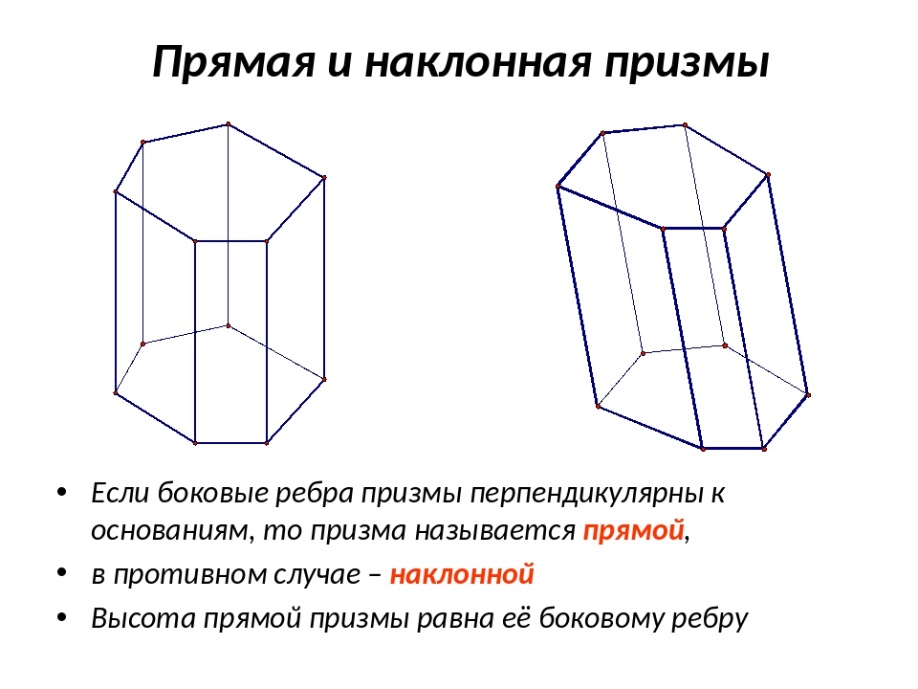
Прямая призма называется ПРАВИЛЬНОЙ, если ее основания являются правильными многоугольниками.
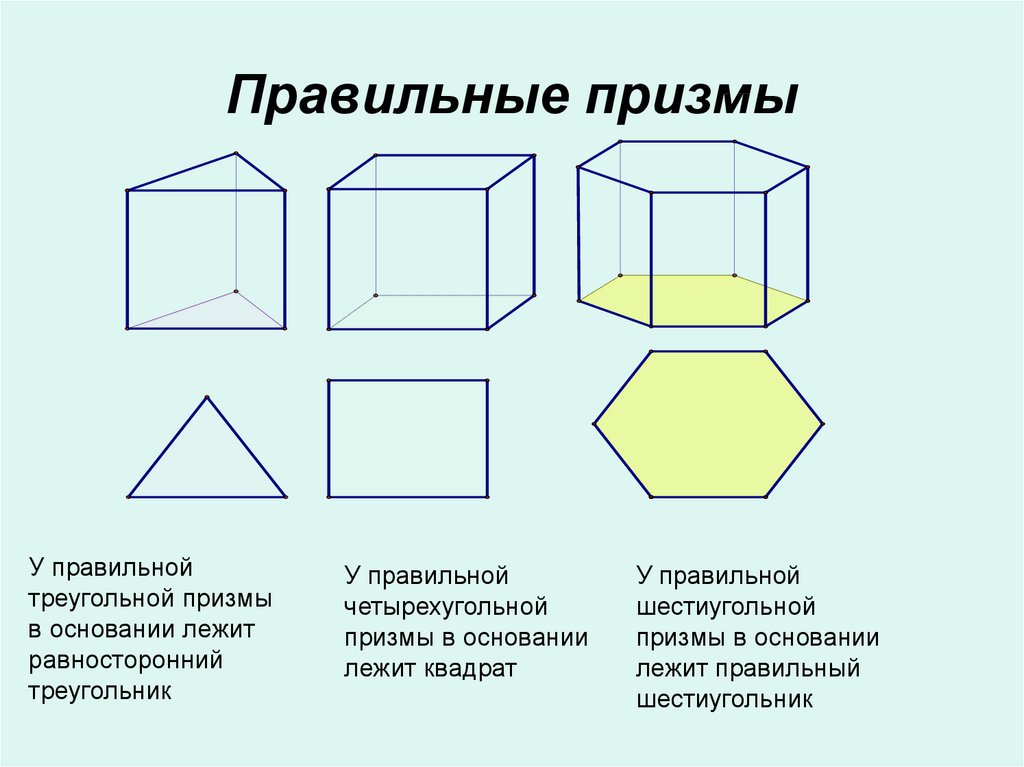
Свойства правильной призмы:
Основания правильной призмы являются правильными многоугольниками.
Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны.
Правильная призма является прямой.
ПАРАЛЛЕЛЕПИПЕД. КУБ.
ПАРАЛЛЕЛЕПИПЕД — это четырёхугольная призма, все грани которой являются параллелограммами.
Грани параллелепипеда, не имеющие общих вершин, называются противоположными.
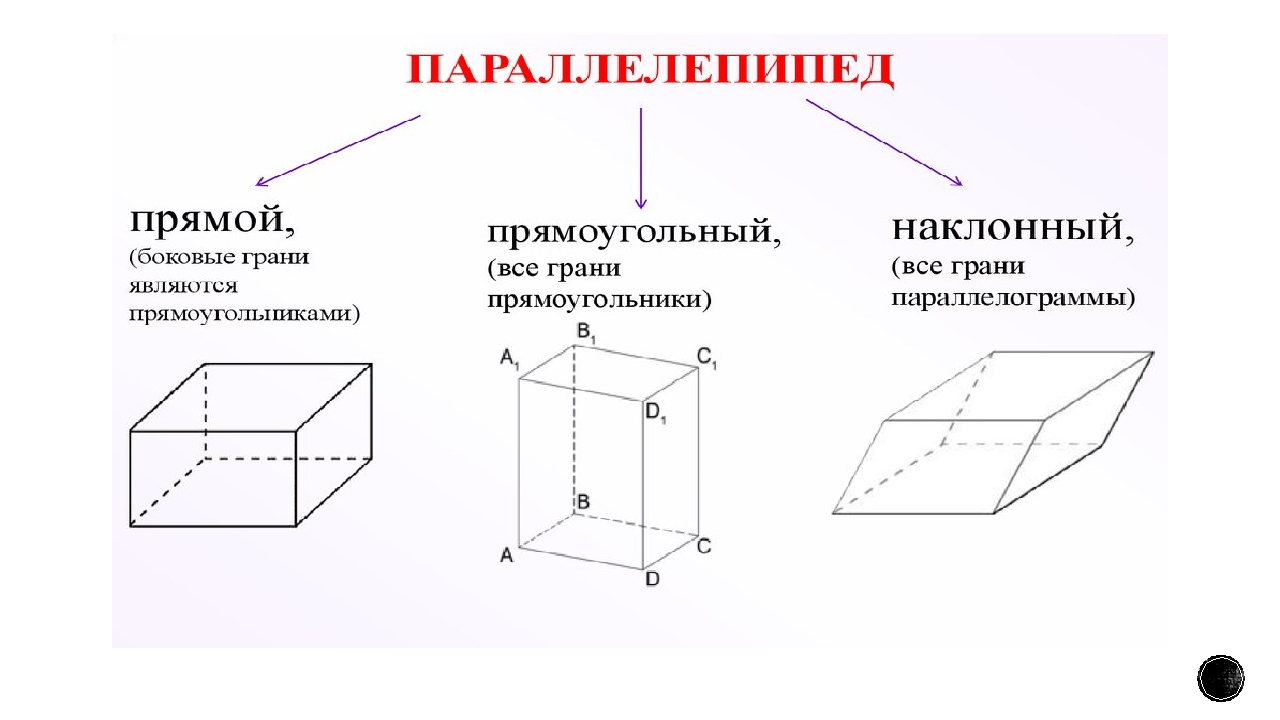
Прямой параллелепипед, у которого основанием является прямоугольник, называется ПРЯМОУГОЛЬНЫМ ПАРАЛЛЕЛЕПИПЕДОМ. У прямоугольного параллелепипеда все грани – прямоугольники.
Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами или измерениями. У прямоугольного параллелепипеда их три: длина a, ширина b, высота c или h.
Прямоугольный параллелепипед, у которого все ребра равны, называется КУБОМ.
Все рёбра куба равны, все грани — квадраты.
Свойства параллелепипеда:
Противоположные грани параллелепипеда параллельны и равны.
Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Боковые грани прямого параллелепипеда — прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений d 2 = a 2 + b 2 + c 2
Площадь поверхности и объём призмы, параллелепипеда и куба.
| Призма | Рисунок | Формулы для объема, площади боковой и полной поверхности |
| Куб | 
| V = a3 Sбок = 4a2 Sполн = 6a2 где a – длина ребра куба |
| Прямоугольный параллелепипед | 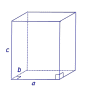
| V = abc Sбок = 2ac + 2bc Sполн = 2ac + 2bc+2ab где
a, b – длины ребер основания параллелепипеда
c - высота параллелепипеда |
| Прямой параллелепипед,
в основании кот. лежит параллелограмм
| 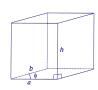
| Sосн = ab sin φ V = Sосн h = abh sin φ Sбок = 2ah + 2bh Sполн = 2ab sin φ + 2ah +2bh где
a, b – длины ребер основания параллелепипеда,
φ – угол между ребрами основания параллелепипеда,
h - высота параллелепипеда. |
| Произвольный параллелепипед | 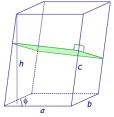
| Sосн = ab sin φ V = Sосн h = abh sin φ V = Sперп с Sбок = Pперп с Sполн = 2ab sin φ + Pперп с где
a, b – длины ребер основания параллелепипеда,
φ – угол между ребрами основания параллелепипеда,
c – длина бокового ребра параллелепипеда,
h - высота параллелепипеда. |
| Продолжить самостоятельно |
| Прямая призма | … | … |
| Правильная призма | … | … |
| Произвольная призма | … | … |



























