Департамент охраны здоровья населения Кемеровской области
Государственное бюджетное профессиональное образовательное учреждение Новокузнецкий филиал
«Кемеровский областной медицинский колледж»
Методическая разработка практического занятия
учебной дисциплины Математика
Раздел 1. Геометрия
Для специальности 34.02.01 Сестринское дело
Занятие № 4
Тема 1. 2 Многогранники, тела вращения. Призма.
Составлена преподавателем
Шилепиной Н. И.
2018 г.
Обучающая цель:
Студент должен знать:
Студент должен уметь:
проводить доказательные рассуждения в ходе решения задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур.
Развивающая цель:
OK 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их выполнение и качество.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
Воспитательная цель:
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать и осуществлять повышение квалификации.
Тип занятия: Выработка и закрепление знаний, умений
Вид занятия: практическое занятие
Междисциплинарные связи: Физика, Информатика и ИКТ
Оснащение занятия:
Литература:
Основные источники:
Математика: алгебра и начала математического анализа, геометрия. 10класс: учеб. для учащихся общеобразоват. организаций (базовый уровень) [Текст] : учебник /под ред. А.Г. Мордкович, И.М. Смирновой. - 10-е изд., стер. – М.: Мнемозина, 2014. – 447 с. : ил.
Математика: алгебра и начала математического анализа, геометрия. 11 класс: учеб. для учащихся общеобразоват. организаций (базовый уровень) [Текст] : учебник / под ред. А.Г. Мордкович, И.М. Смирновой. - 10-е изд., стер. – М. : Мнемозина, 2014. – 429 с. : ил.
Интернет-ресурсы:
Федеральный центр информационно-образовательных ресурсов [Электронный ресурс] // www.fcior.edu.ru. 15.06.2017. – доступ свободный. - заглавие с экрана.
Единая коллекция цифровых образовательных ресурсов [Электронный ресурс] // www.school-collection.edu.ru. - 15.06.2017. – доступ свободный. – заглавие с экрана.
Решу ЕГЭ. Образовательный портал [Электронный ресурс] // https://ege.sdamgia.ru/. 15.06.2017. – доступ свободный. - заглавие с экрана
Онлайн калькулятор [Электронный ресурс] // http://web2.0calc.ru/ 15.06.2017. – доступ свободный. - заглавие с экрана.
Онлайн сервис для построения графиков [Электронный ресурс] // http://www.yotx.ru/. 15.06.2016. – доступ свободный. - заглавие с экрана.
Структура занятия
Организационный момент
Проверка самостоятельной внеаудиторной работы
Постановка целей и задач занятия
Мотивация
Контроль знаний по предыдущей теме
Перерыв
Актуализация базовых знаний. Инструктаж к самостоятельной работе студентов
Самостоятельная работа студентов
Подведение итогов занятия, выставление отметок
Домашнее задание
Ход занятия
| № п/п | Элементы занятия, учебные вопросы | (мин) | Методы и приемы обучения |
-
| Организационный момент | 2 | методы организации и осуществления учебно-познавательной деятельности, вступительное слово |
| 1.1. Приветствие студентов, проверка отсутствующих |
|
| 1.2. Освещение плана занятия |
|
-
| Проверка самостоятельной внеаудиторной работы (приложение 1) | 5 | Устный индивидуальный опрос |
-
| Постановка целей и задач занятия | 2 | методы организации и осуществления учебно-познавательной деятельности |
-
| Мотивация - О каких фигурах шла речь на прошлом уроке? (многогранники) - С какой целью мы изучаем многогранники? (Многие тела, строения в нашем окружении имеют форму многогранников, поэтому для построения зданий, изучения каких-то явлений нужно знать свойство многогранников, уметь различать их по форме) - Все ли мы узнали о многогранниках на прошлом уроке? (Нет) - Поставьте перед собой цели, которые вы будете достигать на протяжении всего урока. (Продолжить работу по изучению темы «Многогранники». Мы мало внимания уделили Призме, на лекции познакомились только с элементами призмы, следовательно, продолжить изучение этой темы, а также продолжить решать задачи по данной теме). - Итак, сегодня на уроке мы продолжим работу по изучению темы «Многогранники. Призма». Узнаем много интересного из мира многогранников, рассмотрим виды призм, и, конечно же, научимся решать задачи. А урок начнем с контроля знаний по теме «Параллелепипед и куб».
| 2 | методы стимулирования и мотивации учебной деятельности, сообщающее слово |
-
| Контроль знаний по предыдущей теме (приложение 2) | 15 | Математический диктант |
-
| Перерыв (проветривание аудитории, физкультминутка) | 5 | Здоровьесбережение |
-
| Актуализация базовый знаний: На данном уроке рассмотрим решение задач по теме «Призма». В начале занятия мы повторим основные сведения, свойства призмы и ее разновидности: наклонная, прямая и правильная. Затем решим самостоятельно несколько типовых задач. - Итак, что называют призмой? Определение: Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её основаниями. Многоугольник лежащий в основании определяет название призмы: треугольник — треугольная призма, четырёхугольник — четырёхугольная; пятиугольник — пятиугольная и т.д. - Что называют высотой призмы? Определение: Отрезок, соединяющий плоскости, в которых лежат основания призмы перпендикулярный этим плоскостям. - Что называют диагональю призмы? Определение: Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. - Какие виды призм вы знаете? Прямая призма, наклонная призма, правильная призма. - Какую призму называют прямой? Определение. Прямая призма - это такая призма, у которой боковое ребро перпендикулярно плоскости основания и каждая боковая грань – это прямоугольник. - Какую призму называют наклонной? Если боковое ребро призмы не перпендикулярно плоскости ее основания, то такую призму называют наклонной. - Какую призму называют правильной? Определение. Правильной называется такая прямая призма, в основании которой лежит правильный n-угольник. Самостоятельная работа: Итак, работа состоит из 5 задач. На выполнение работы отводится 40 минут. Ответы к заданиям запишите в виде полного решения, включая дано, рисунок и слово «Ответ». Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо указать только номер соответствующего задания. Начать решения советую с тех заданий, которые вызывают меньше затруднений, затем переходите к другим заданиям. Для экономии времени пропускайте задания, которые не удается решить сразу и переходите к следующему. Если у вас останется время вы сможете вернутся к пропущенным заданиям. Все необходимые вычисления выполняйте в черновике. А теперь переходим к выполнению самостоятельной работы. |
10 | Изучение инструкции - прием |
-
| Выполнение самостоятельной работы. Во время самостоятельной работы преподаватель контролирует работу студентов, исправляет ошибки, неточности, дает рекомендации, советы
| 42 | Индивидуальная работа
|
-
| Подведение итогов занятия - Итак, мы повторили теорию и решили некоторые типовые задачи по теме «Призма». На следующем уроке мы перейдём к изучению пирамиды. Выставление отметок | 5 | методы организации и осуществления учебно-познавательной деятельности, |
-
| Домашнее задание: Повторить лекцию по теме «Пирамида. Правильные многогранники» Принести СРС практической работы «Построение простейших сечений куба, призмы, пирамиды» Уч. 10кл.: 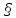 51, № 51.9. 51, № 51.9. | 2 | методы организации и осуществления учебно-познавательной деятельности, |
ПРИЛОЖЕНИЕ 1
Проверка самостоятельной внеаудиторной работы
Выступление с сообщениями на тему: «Правильные и полуправильные многогранники».
ПРИЛОЖЕНИЕ 2
Контроль знаний по теме «Параллелепипед и куб»
Математический диктант
Запишите ребра, равные AK.
Запишите ребра, выходящие из вершины К.
Запишите грань равную KPME.
Запишите грани, которым принадлежит ребро EM.
Запишите формулу объема прямоугольного параллелепипеда.
Запишите формулу полной поверхности параллелепипеда.
Запишите формулу объема куба.
Запишите формулу площади полной поверхности куба.
Вычислите объем данного параллелепипеда.
Дан куб. укажите количество скрещивающихся ребер с ребром AD.
| 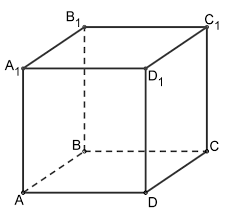
Рисунок 1 | 
Рисунок 2 |
Критерий оценивания:
9-10 правильных ответов оценка «5»
8 правильных ответов оценка «4»
7 правильных ответов оценка «3»
Менее 7 правильных ответов оценка «2»
Эталоны ответов
DE, BP, CM.
KE, KP, KA.
ABCD.
EMPK, EMCD.
V = abc.
S = 2(ab+bc+ac).
V = a3.
S = 6a2.
150
2
ПРИЛОЖЕНИЕ 3
Самостоятельная работа по теме: «Призма. Решение задач.»
| Задача № 1. 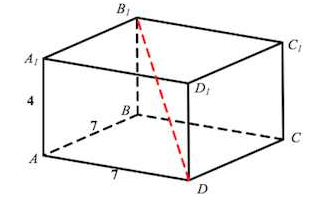
| Найдите квадрат расстояния между вершинами D и B1 прямоугольного параллелепипеда, для которого 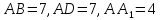 . . |
| Задача № 3. 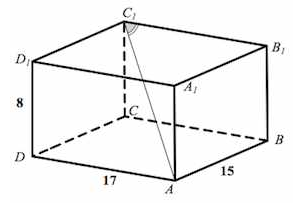
| Найдите угол 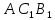 прямоугольного параллелепипеда, для которого прямоугольного параллелепипеда, для которого 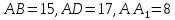 . Ответ дайте в градусах. . Ответ дайте в градусах. |
| Задача № 4. 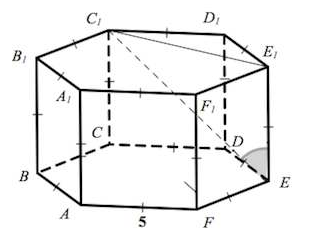
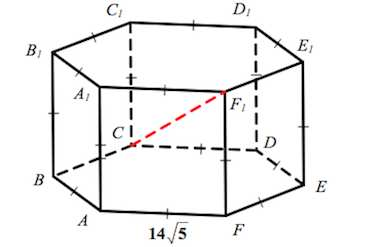
| В правильной шестиугольной призме 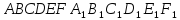 все ребра равны все ребра равны 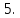 Найдите угол Найдите угол 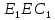 . . |
| Задача № 5. 
| В правильной шестиугольной призме 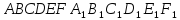 все ребра равны все ребра равны 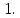 Найдите угол между прямыми Найдите угол между прямыми 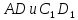 . Ответ дайте в градусах. . Ответ дайте в градусах. |
Эталоны к решению задач
114;
70;
450;
600;
450.
Критерий оценивания задач:
7 – 8 правильное решенные задачи оценка «5»;
6 – правильно решенных задач оценка «4»;
5 – правильно решенных задачи оценка «3»;
Менее 5 правильно решенных задач оценка «2».







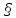 51, № 51.9.
51, № 51.9.


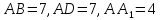 .
.
 все ребра равны
все ребра равны 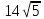 . Найдите расстояние между точками
. Найдите расстояние между точками 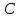 и
и 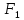 .
.
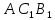 прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 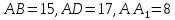 . Ответ дайте в градусах.
. Ответ дайте в градусах.
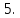 Найдите угол
Найдите угол 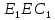 .
.
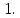 Найдите угол между прямыми
Найдите угол между прямыми 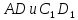 . Ответ дайте в градусах.
. Ответ дайте в градусах.


















