МКОУ «Днепровская СШ»
Индивидуальный проект
Формула Пика
Выполнил: ученица 9 класса
Старикова Анстасия
Руководитель: Роженкова Лариса Владимировна,
учитель математики
с. Днепровское
2021 год
ОГЛАВЛЕНИЕ
| 1. Введение | 3 - 4 |
| 2. Основная часть | 5 - 8 |
| 2.1. Формула Пика. Решетки. Узлы | 5 - 6 |
| 2.2. Доказательство формулы Пика | 6 - 8 |
| 3. Практическая часть | 9 - 13 |
| 3.1.Исследование площадей многоугольников, изображенных на клетчатой бумаге | 9 - 12 |
| 3.2. Геометрические задачи с практическим содержанием | 13 |
| 3. Заключение | 14 |
| 4. Литература | 15 |
| 5. Приложение | 16 - 18 |
| 1.Задачи на нахождение площади многоугольника на клетчатой бумаге по формуле Пика | 16 - 17 |
| 2. Задачи – рисунки, для которых применима формула Пика | 18 |
Введение
«Берем палец и считаем»
В.В.Вавилов
Нарисуйте, пожалуйста, сложный невыпуклый многоугольник на клетчатой бумаге, а я вам в уме за полминуты найду площадь этой фигуры.
Увлечение математикой часто начинается с размышления над какой-то задачей. Увидев задачи в контрольно – измерительных материалах ОГЭ на нахождение площади многоугольника на клетчатой бумаге, я решила их исследовать. Возникли вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге. Может есть какой-то метод для нахождения площади фигуры, изображённой на клетчатой бумаге? Ведь, если фигура состоит из целых квадратиков, это сделать довольно таки легко. Посчитать квадратики и всё! А когда квадратик не целый, что делать? Я подумала, что решения таких задач должны существовать и должны быть оригинальны, красивы и часто проще и быстрее, чем аналитическим путем.
Так и была определена тема для моего проекта.
Объект проекта: задачи на клетчатой бумаге.
Предмет проекта: задачи на вычисление площади многоугольника на клетчатой бумаге, методы и приёмы их решения.
Актуальность: данная тема является дополнением и углублением в курс геометрии; формула Пика поможет лучше подготовиться к олимпиадам и экзаменам.
Методы исследования: моделирование, построение, анализ и классификация информации, сравнение, обобщение.
Работа имеет практическое применение. Ее могут использовать школьники и взрослые при решении реальных ситуаций; учителя, как при проведении уроков по математике, так и на факультативных курсах и дополнительных занятий на повторение.
Цель проекта:
Изучить формулу Пика для вычисления площадей многоугольников на клетчатой бумаге.
Для достижения поставленной цели предусматривается решение следующих задач:
-
Подобрать необходимую литературу.
-
Отобрать материал для исследования, выбрать главную, интересную, понятную информацию.
-
Проанализировать и систематизировать полученную информацию.
-
Найти различные методы и приёмы решения задач на клетчатой бумаге.
-
Создать электронную презентацию с заданиями на применение формулы Пика.
Гипотеза: Площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по формуле планиметрии.
При решении задач на клетчатой бумаге понадобится геометрическое воображение и достаточно простые геометрические сведения, которые известны всем. При более внимательном исследовании задач на клетчатой бумаге, убеждаешься в их востребованности, оригинальности, полезности, возникает ощущение красоты, закона и порядка в природе.
2. Основная часть
2.1. Формула Пика. Решетки. Узлы
При решении задач на клетчатой бумаге необходимы понятия решетки и узла.
Клетчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости.
Рассмотрим на плоскости два семейства параллельных прямых, разбивающих плоскость на равные квадраты. Любой из этих квадратов называется фундаментальным квадратом или квадратом, порождающим решетку. Множество всех точек пересечения этих прямых называется точечной решеткой или просто решеткой, а сами точки –узлами решетки.
Рис.1.
Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу)
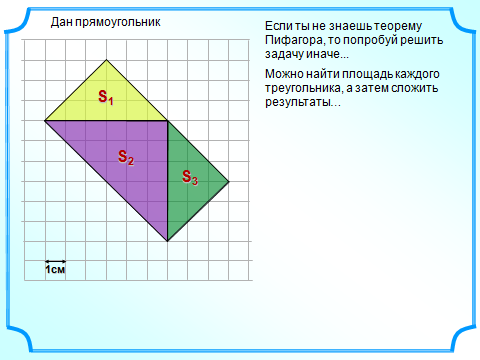
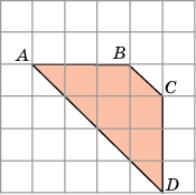
А также, площадь любого многоугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим ч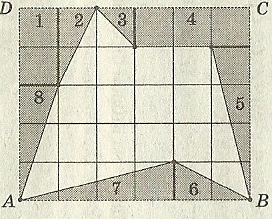 ерез вершины нарисованного треугольника. Чтобы вычислить площадь многоугольника, изображенного на рисунке, необходимо достроить его до прямоугольникаABCD, вычислить площадь прямоугольника ABCD, найти площадь заштрихованной фигуры как сумму площадей треугольников и прямоугольников её составляющих, вычесть её из площади прямоугольника. И хотя многоугольник и выглядит достаточно просто, для вычисления его площади нам придется потрудиться. А если бы многоугольник выглядел более причудливо, как на следующих рисунках?
ерез вершины нарисованного треугольника. Чтобы вычислить площадь многоугольника, изображенного на рисунке, необходимо достроить его до прямоугольникаABCD, вычислить площадь прямоугольника ABCD, найти площадь заштрихованной фигуры как сумму площадей треугольников и прямоугольников её составляющих, вычесть её из площади прямоугольника. И хотя многоугольник и выглядит достаточно просто, для вычисления его площади нам придется потрудиться. А если бы многоугольник выглядел более причудливо, как на следующих рисунках?
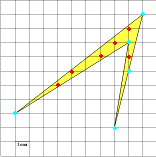
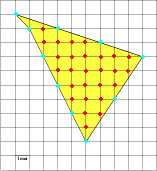
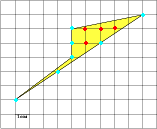

Оказывается, площади многоугольников, вершины которых расположены в узлах решетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика: S = В +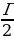 - 1, где S– площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.
- 1, где S– площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.
2.2. Доказательство формулы Пика.
Пусть В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины, 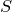 — его площадь. Тогда справедлива формула Пика:
— его площадь. Тогда справедлива формула Пика: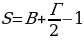 .
.
Покажу справедливость формулы Пика. Сначала заметим, что формула Пика верна для единичного квадрата.
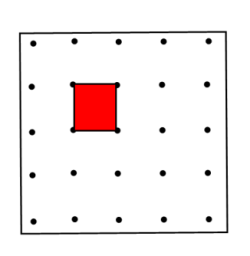
Действительно, в этом случае имеем: В=0, Г=4 иS=0+4/2-1=1. Фундаментальный квадрат порождает решетку, то есть решетку можно построить следующим образом. Отметим вершины квадрата. Затем сдвинем его параллельно одной из его сторон на длину этой стороны и отметим две вновь полученные вершины.
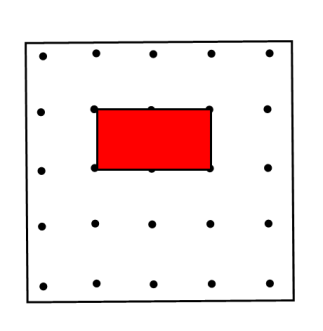
Если этот процесс продолжать сначала в одном направлении до длины a, а затем полученную полоску сдвинуть параллельно себе в направлении другой стороны квадрата на длину этой стороны до длины b, то получим решетку.
а
b
Причем, число узлов решетки, лежащих внутри решетки,
В = (а-1)(b-1), а число узлов решетки, расположенных на его границе,
Г = 2a + 2b.
 Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны
Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны 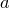 и
и 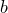 . Имеем в этом случае, В=(а-1)(b-1), Г=2a+2b, тогда по формуле Пика S= (a -1)(b-1) +
. Имеем в этом случае, В=(а-1)(b-1), Г=2a+2b, тогда по формуле Пика S= (a -1)(b-1) +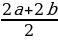 -1 =ab-a-b+1+a+b-1=ab. Получили формулу площади прямоугольника со сторонами a, b.
-1 =ab-a-b+1+a+b-1=ab. Получили формулу площади прямоугольника со сторонами a, b.
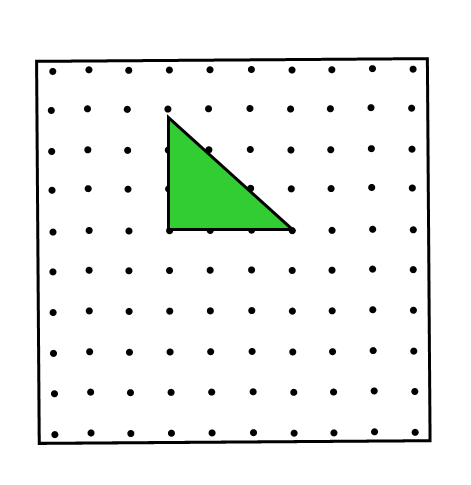 Рассмотрим теперь прямоугольный треугольник с катетами a и b. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая,
Рассмотрим теперь прямоугольный треугольник с катетами a и b. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая,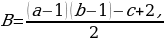 Г=
Г=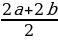 +с-1 и получаем, что S =
+с-1 и получаем, что S = 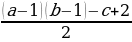 +
+ 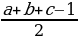 -1 =
-1 = 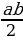 -
- 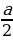 -
- 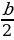 -
- 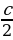 +
+ 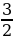 +
+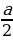 +
+ 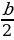 +
+ 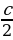 -
- 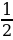 - 1 =
- 1 = 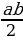 . Таким образом, получили формулу для вычисления площади прямоугольного треугольника. Значит, формула Пика верна для прямоугольного треугольника.
. Таким образом, получили формулу для вычисления площади прямоугольного треугольника. Значит, формула Пика верна для прямоугольного треугольника.
Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник. Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.
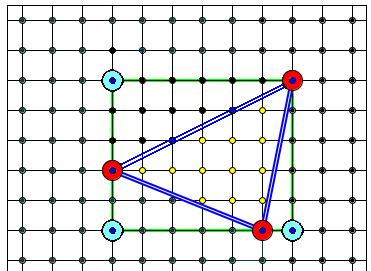
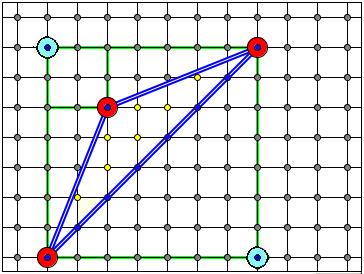
Рис.2.
3. Практическая часть
3.1.Исследование площадей многоугольников, изображенных на клетчатой бумаге
Приведу несколько примеров из заданий ОГЭ на нахождение площадей многоугольников.
| 1)На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник. Найдите его площадь в квадратных сантиметрах |
| Рисунок | По формуле геометрии | По формуле Пика |
|  
| a=6; b=4 S1 = 1*5: 2 = 2,5. S2=5*5:2 = 12,5 S = 2,5 + 12,5 = 15(см2) | 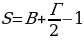
Г=12,B=10 . S=10+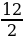 -1=15(см2) -1=15(см2)
|
| 2) На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольникABC.Найдите его площадь в квадратных сантиметрах. |
| Рисунок | По формуле геометрии | По формуле Пика |
| 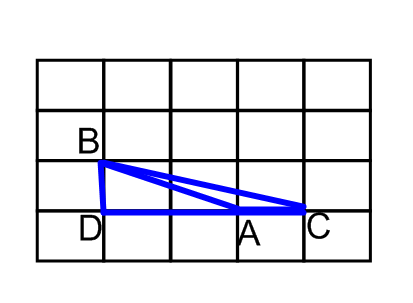
| S1 = 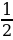 ∙ 3 ∙ 1 = 1,5 ∙ 3 ∙ 1 = 1,5 S2 = 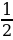 ∙ 2 ∙ 1 = 1 см2 ∙ 2 ∙ 1 = 1 см2 S = 1,5 – 1 = 0,5(см2) | 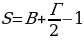
Г=3, В=0. S=0+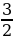 -1=0,5(см2) -1=0,5(см2) |
|
|
|
|
| 4)На клетчатой бумаге с клетками размером 1 см х 1 см изображен четырехугольникABCD. Найдите его площадь в квадратных сантиметрах. |
| Рисунок | По формуле геометрии | По формуле Пика |
| 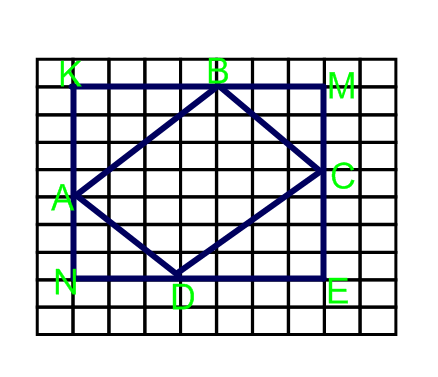
| Sкв.KMEN=7 7=49 7=49 Sтр.AKB=1/2 KB KB AK=1/2 AK=1/2 4 4 4=8 4=8 Sтр.DCE=1/2∙ DE∙CE = ½ ∙ 4 ∙ 4 =8 Sтр.AND= 1/2 ND ND AN=1/2 AN=1/2 3 3 3=4,5 3=4,5 Sтр.BMC=1/2∙BM ∙ CM= ½ ∙ 3∙3=4,5 SABCD=49-8-8-4,5-4,5=24см2 | 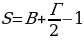
В=18, Г=14 S=18+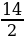 -1=24 см2 -1=24 см2 |
| 3)На клетчатой бумаге с клетками размером 1 см х 1 см изображен четырех угольник. Найдите его площадь в квадратных сантиметрах |
| Рисунок | По формуле геометрии | По формуле Пика |
| 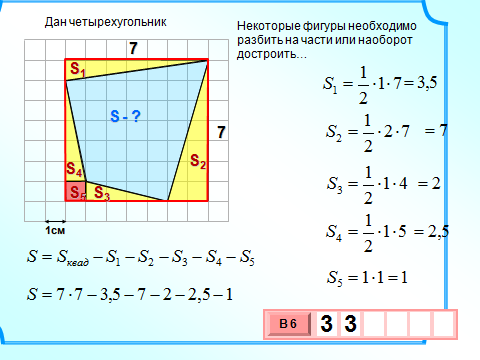
| S1=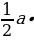 b=1/2 b=1/2 7 7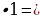 3,5 3,5 S2=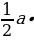 b=1/2 b=1/2 7 7 2=7 2=7 S3=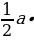 b=1/2 b=1/2 4 4 1=2 1=2 S4=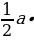 b=1/2 b=1/2 5 5 1=2,5 1=2,5 S5=a²=1²=1 Sкв.= a²=7²=49 S=49-3,5-7-2-2,51=33(см²) | 
Г=4;В=32. S=32+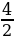 -1=33см² -1=33см² |
| 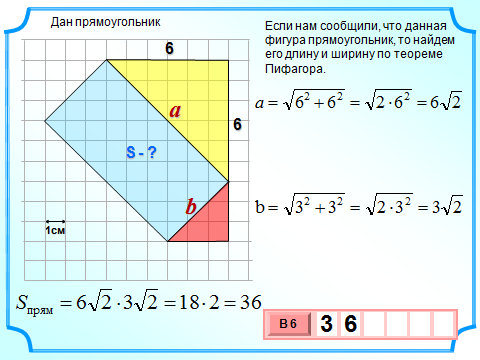
| S=a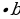 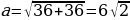
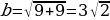
S=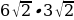 =36 см2 =36 см2
| 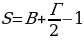
Г=18, В=28 S=28+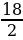 -1=36см2 -1=36см2 |
| 5)На клетчатой бумаге с клетками размером 1 см х 1 см изображен четырех угольник. Найдите его площадь в квадратных сантиметрах |
| Рисунок | По формуле геометрии | По формуле Пика |
| 
| S1=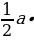 b=1/2 b=1/2 3 3 6=9 6=9 S2=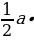 b=1/2 b=1/2 6 6 6=18 6=18 S3=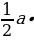 b=1/2 b=1/2 3 3 6=9 6=9 S=9+18+9=36см² | 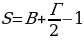
Г=18;В=28. S=28+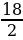 -1=36см² -1=36см² |
| 6)На клетчатой бумаге с клетками размером 1 см х 1 см изображен четырех угольник. Найдите его площадь в квадратных сантиметрах |
| Рисунок | По формуле геометрии | По формуле Пика |
| 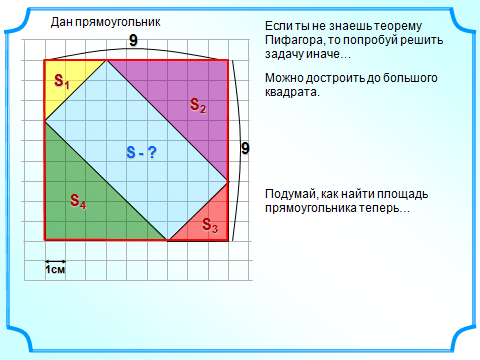
| S1=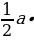 b=1/2 b=1/2 3 3 3=4,5 3=4,5 S2=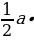 b=1/2 b=1/2 6 6 6=18 6=18 S3=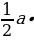 b=1/2 b=1/2 3 3 3=4,5 3=4,5 S4=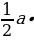 b=1/2 b=1/2 6 6 6=18 6=18 Sкв.=9²=81см² S=81-4,5-18-4,5-18=36см² | 
Г=18;В=28. S=28+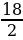 -1=36см² -1=36см² |
| 7)На клетчатой бумаге с клетками размером 1 см х 1 см изображен четырех угольник. Найдите его площадь в квадратных сантиметрах |
| Рисунок | По формуле геометрии | По формуле Пика |
| 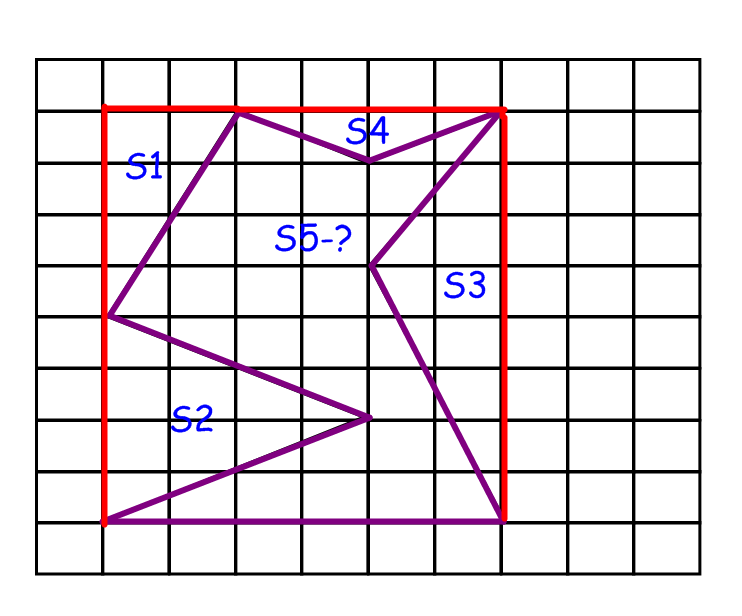
| S1=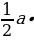 b=1/2 b=1/2 2 2 4=4 4=4 S2=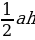 =1/2 =1/2 4 4 4=8 4=8 S3= =1/2 =1/2 8 8 2=8 2=8 S4=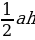 =1/2 =1/2 4 4 1=2 1=2 Sпр.=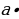 b=6 b=6 8=48 8=48 S5=48-4-8-8-2=26см² | 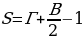
Г=18;В=18. S=18+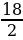 -1=26см² -1=26см² |
Вывод: Таким образом, рассматривая задачи на нахождение площадей многоугольников, изображенных на клетчатой бумаге, по формулам геометрии и по формуле Пика и сравнивая результаты в таблицах, я показала справедливость формулы Пика и пришла к выводу, что площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по формуле геометрии.
Итак, моя гипотеза оказалась верной.
Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на бесконечном листке бумаги, расчерченном на одинаковые квадратики? Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Я научилась вычислять площади многоугольников, нарисованных на клетчатом листке.
Для многих задач на бумаге в клетку нет общего правила решения, конкретных способов и приёмов. Вот это их свойство обуславливает их ценность для развития не конкретного учебного умения или навыка, а вообще умения думать, размышлять, анализировать, искать аналогии, то есть, эти задачи развивают мыслительные навыки в самом широком их понимании.
3.2.Геометрические задачи с практическим содержанием.
Поможет нам формула Пика и для решения геометрических задач с практическим содержанием.
З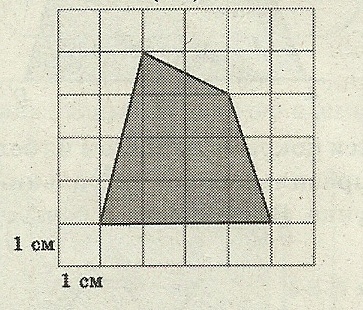 адача 1. Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м (рис. 3)
адача 1. Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м (рис. 3)
Решение. Найдём S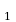 площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика:
площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика:
S = В + 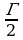 - 1
- 1
Рис. 3 В = 8, Г = 7. S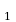 = 8 + 7/2 – 1 = 10,5 (см²)
= 8 + 7/2 – 1 = 10,5 (см²)
1 см² - 200² м²; S = 40000 · 10,5 = 420 000 (м²)
 Ответ: 420 000 м²
Ответ: 420 000 м²
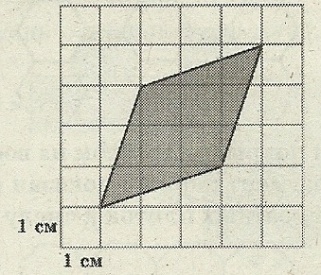
Задача 2. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м. (рис. 4)
Рис. 4
Решение. Найдём S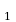 площадь четырёхугольника изображенного на клетчатой бумаге по формуле Пика: S = В +
площадь четырёхугольника изображенного на клетчатой бумаге по формуле Пика: S = В + 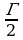 - 1
- 1
В = 7, Г = 4. S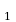 = 7 + 4/2 – 1 = 8 (см²)
= 7 + 4/2 – 1 = 8 (см²)
1 см² - 200² м²; S = 40000 · 8 = 320 000 (м²)
Ответ: 320 000 м²
З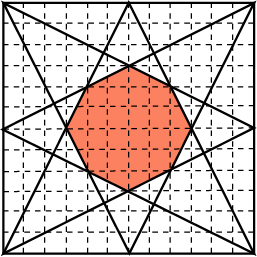 адача 3. Вершины квадрата соединены с серединами его сторон, как показано на рисунке 5. Найдите площадь закрашенного восьмиугольника, если стороны квадрата равны 12.
адача 3. Вершины квадрата соединены с серединами его сторон, как показано на рисунке 5. Найдите площадь закрашенного восьмиугольника, если стороны квадрата равны 12.
Рис. 5. Решение: По формуле Пика: S= В + Г /2 – 1. В = 21,
Г = 8, S = 21 + 8 / 2 – 1 = 24 (кв.ед.)
Заключение
В процессе исследования я изучила справочную, научно-популярную литературу. Узнала, что задача на нахождение площади многоугольника с вершинами в узлах сетки сподвигла австрийского математика Пика в 1899 году доказать замечательную формулу Пика.
В результате моей работы я расширила свои знания о решении задач на клетчатой бумаге, определила для себя классификацию исследуемых задач, убедилась в их многообразии.
Я научилась вычислять площади многоугольников, изображенных на клетчатом листке. Рассмотренные задания имеют различный уровень трудности – от простых до олимпиадных. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных. Такой способ нахождения площадей многоугольников, изображенных на клетчатой бумаге, можно использовать на ОГЭ для решения задач.
Клетчатая бумага позволяет проводить многие геометрические построения, помогает лучше понять и изучить свойства фигур. Упражнения на клетчатой бумаге способствуют развитию интуиции, воображения, памяти, внимания.
Литература
-
Свободная энциклопедия Википедия, статья «Формула Пика», URL: https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%9F%D0%B8%D0%BA%D0%B0
-
Свободная энциклопедия Википедия, статья «Пик, Георг», URL: https://ru.wikipedia.org/wiki/%D0%9F%D0%B8%D0%BA,_%D0%93%D0%B5%D0%BE%D1%80%D0%B3
-
Научно-популярный физико-математический журнал «Квант», Н.Б.Васильев, статья «Вокруг формулы Пика», URL:http://kvant.ras.ru/1974/12/vokrug_formuly_pika.htm
-
Математика, которая мне нравится[электронный ресурс], статья «Формула Пика», URL:http://hijos.ru/2011/09/14/formula-pika/
-
Математика, которая мне нравится [электронный ресурс], статья «Георг Александр Пик (1859-1942)», URL: http://hijos.ru/2011/12/30/georg-aleksandr-pik-1859-1942/
-
Справочный портал Калькулятор, статья «Многоугольник. Формула Пика», URL: https://www.calc.ru/Kubicheskiye-Uravneniya-Formula-Pika.html
ПРИЛОЖЕНИЕ
Приложение 1.
Задачи на нахождение площади многоугольника на клетчатой бумаге по формуле Пика.
Задача 1.
Найдите площадь прямоугольника АВСD (рис.1).
Р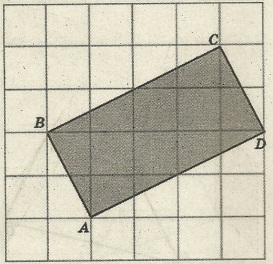 ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В + 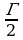 - 1 .
- 1 .
В = 8, Г = 6
S = 8 + 6/2 – 1 = 10 (см²)
Ответ: 10 см².
Рис. 1
Задача 2. Найдите площадь параллелограмма АВСD (рис.2)
Р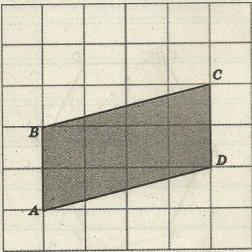 ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В + 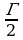 - 1 .
- 1 .
В = 6, Г = 6
S = 6 + 6/2 – 1 = 8 (см²)
Ответ: 8 см².
Рис. 2
Задача 3. Найдите площадь треугольника АВС (рис.3)
Р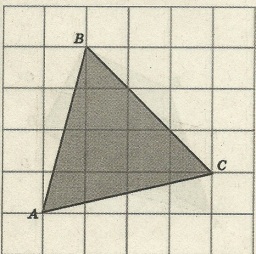 ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В + 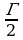 - 1 .
- 1 .
В = 6, Г = 5
S
Рис. 3
= 6 + 5/2 – 1 = 7,5 (см²). Ответ: 7,5 см².
Задача 4. Найдите площадь четырёхугольника АВСD (рис. 4)
Р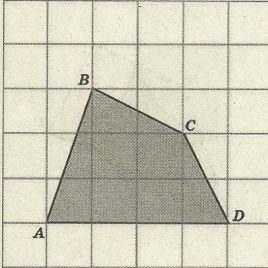 ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В + 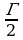 - 1 .
- 1 .
В = 5, Г = 7
S = 5 + 7/2 – 1 = 7,5 (см²)
Ответ: 7,5 см².
Рис. 4
З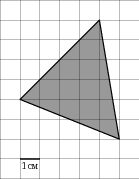 адача 5. На клетчатой бумаге с клетками размером 1 см
адача 5. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (рис. 6). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (рис. 6). Найдите его площадь в квадратных сантиметрах.
Решение. По формуле Пика: S = В + 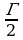 - 1 .
- 1 .
В = 12, Г = 6
S = 12 + 6/2 – 1 = 14 (см²). Ответ: 14
Рис. 6
Задача 2. На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (рис. 7). Найдите ее площадь в квадратных сантиметрах.
1 см изображена трапеция (рис. 7). Найдите ее площадь в квадратных сантиметрах.
Р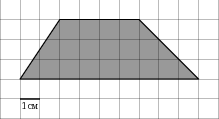 ешение. Воспользуемся формулой Пика:
ешение. Воспользуемся формулой Пика:
В = 12, Г = 17
S = 12 + 17/2 – 1 = 19,5 (см²)
О
Рис. 7
твет: 19,5
Приложение 2
Задачи – рисунки, для которых применима формула Пика
Найти площадь изображенного на рисунке многоугольника:








 ерез вершины нарисованного треугольника. Чтобы вычислить площадь многоугольника, изображенного на рисунке, необходимо достроить его до прямоугольникаABCD, вычислить площадь прямоугольника ABCD, найти площадь заштрихованной фигуры как сумму площадей треугольников и прямоугольников её составляющих, вычесть её из площади прямоугольника. И хотя многоугольник и выглядит достаточно просто, для вычисления его площади нам придется потрудиться. А если бы многоугольник выглядел более причудливо, как на следующих рисунках?
ерез вершины нарисованного треугольника. Чтобы вычислить площадь многоугольника, изображенного на рисунке, необходимо достроить его до прямоугольникаABCD, вычислить площадь прямоугольника ABCD, найти площадь заштрихованной фигуры как сумму площадей треугольников и прямоугольников её составляющих, вычесть её из площади прямоугольника. И хотя многоугольник и выглядит достаточно просто, для вычисления его площади нам придется потрудиться. А если бы многоугольник выглядел более причудливо, как на следующих рисунках?






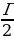 - 1, где S– площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.
- 1, где S– площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.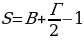 .
.

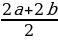 -1 =ab-a-b+1+a+b-1=ab. Получили формулу площади прямоугольника со сторонами a, b.
-1 =ab-a-b+1+a+b-1=ab. Получили формулу площади прямоугольника со сторонами a, b. Рассмотрим теперь прямоугольный треугольник с катетами a и b. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая,
Рассмотрим теперь прямоугольный треугольник с катетами a и b. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая,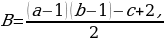 Г=
Г=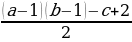 +
+ 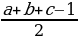 -1 =
-1 = 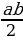 -
- 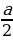 -
- 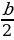 -
- 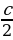 +
+ 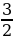 +
+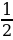 - 1 =
- 1 = 



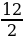 -1=15(см2)
-1=15(см2)

 7=49
7=49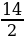 -1=24 см2
-1=24 см2
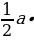 b=1/2
b=1/2 3,5
3,5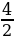 -1=33см²
-1=33см²
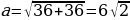
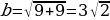
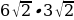 =36 см2
=36 см2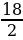 -1=36см2
-1=36см2


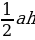 =1/2
=1/2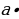 b=6
b=6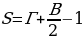
 адача 1. Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м (рис. 3)
адача 1. Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м (рис. 3)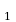 площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика:
площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: 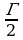 - 1
- 1 Ответ: 420 000 м²
Ответ: 420 000 м² адача 3. Вершины квадрата соединены с серединами его сторон, как показано на рисунке 5. Найдите площадь закрашенного восьмиугольника, если стороны квадрата равны 12.
адача 3. Вершины квадрата соединены с серединами его сторон, как показано на рисунке 5. Найдите площадь закрашенного восьмиугольника, если стороны квадрата равны 12.  ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В +  ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В +  ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В +  ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В +  адача 5. На клетчатой бумаге с клетками размером 1 см
адача 5. На клетчатой бумаге с клетками размером 1 см ешение. Воспользуемся формулой Пика:
ешение. Воспользуемся формулой Пика:



































