Государственное бюджетное образовательное учреждение
«Починковский сельскохозяйственный техникум»
Индивидуальный проект по математике
на тему:
«Геометрические парадоксы»
Проект выполнил:
обучающийся 1ТО группы
Фуфаев Александр
Руководитель:
преподаватель математики
Абросимова Е.А.
с.Починки, 2017 г.
Содержание
| 1) | Введение | 3 |
| 2) | Парадоксы в геометрии | 4 |
| 3) | Многообразие и примеры парадоксов | 6 |
| 4) | Заключение | 15 |
| 5) | Информационные ресурсы | 16 |
Введение
Парадокс в широком смысле - это утверждение, резко расходящееся с общепринятыми, устоявшимися мнениями, отрицание того, что представляется «безусловно, правильным». А в более узком и современном значении – это просто два противоположных утверждения, для каждого из которых имеются представляющиеся убедительными аргументы.
Особое место занимают парадоксы в математике и логике, так как «чистая математика» - абстрактная наука, построенная на теориях, которые не кажутся очевидными с первого взгляда. Здесь их статус глубоких и кардинальных проблем не подвергается сомнению. Тем более что в математике, как ни в одной другой науке, особое внимание обращается на строгость и логическую последовательность доказательств. При этом часто возникают ситуации, в которых рассуждения, применяющиеся совсем недавно и считающиеся строгими, будут требовать дополнительного обоснования.
Цели и задачи
Цель моей работы, это рассмотреть понятие «парадоксов», их виды, а также проблемы парадоксов в математике и их значение для развития наук.
А задачей моей работы является узнать как можно больше информации, задачи и их решения, а также примеры парадоксов.
Парадоксы в геометрии
Парадокс - это два противоположных утверждения, для каждого из которых имеются представляющиеся убедительными аргументы.
Парадоксы были типичными способами постановки проблем в античном мышлении. Сначала парадоксы рассматривались только как продукт философских измышлений, теперь наука признала их полноправными членами сообщества научных проблем.
Парадоксы возникают в современных прикладных науках также часто, как и в древних. В свое время вавилонские жрецы - астрологи заметили, что некоторые планеты временами замедляют движение, пятятся назад, а затем снова продолжают движение в обычном направлении. Гераклид Понтийский смог объяснить "явление блуждающих светил" с помощью математической теории эпицикла. Но при этом оставались другие проблемы - не все светила вели себя по этой схеме. Долгое время ученые с помощью своих теорий не могли объяснить «дуализм света», только предположение Д.К. Максвелла об электромагнитной природе света разрешило эту проблему. Таким образом, можно считать, что парадоксы возникают в науке там, где теория не описывает процессы должным образом. Разрешение таких парадоксальных явлений ведет в свою очередь к возникновению новых теорий.
Все парадоксы имеют одно общее свойство - самоприменимость (циркулярность). В каждом из них объект, о котором идет речь, характеризуется посредством некоторой совокупности объектов, к которой он сам принадлежит. Если мы выделяем, например, самого хитрого человека, мы делаем это при помощи совокупности людей, к которой относится и данный человек. И если говорим: "Это высказывание ложно", мы характеризуем интересующее нас высказывание путем ссылки на включающую его совокупность всех ложных высказываний. Во всех парадоксах имеет место самоприменимость понятий, а значит, есть как бы движение по кругу, приводящее, в конце концов, к исходному пункту. Стремясь охарактеризовать интересующий нас объект, мы обращаемся к той совокупности объектов, которая включает его. Однако оказывается, что сама она для своей определенности нуждается в рассматриваемом объекте и не может быть ясным образом понята без него. В этом круге, возможно, и кроется источник парадоксов.
Следует обратить внимание на одно важное различие. Устранение парадоксов и их разрешение - это вовсе не одно и то же.
Устранить парадокс из некоторой теории - значит перестроить ее так, чтобы парадоксальное утверждение оказалось в ней недоказуемым.
Каждый парадокс опирается на большое число определений, допущений и аргументов. Его вывод в теории представляет собой некоторую цепочку рассуждений. Формально говоря, можно подвергнуть сомнению любое ее звено, отбросить его и тем самым разорвать цепочку и устранить парадокс. Во многих работах так и поступают и этим ограничиваются. Но это еще не разрешение парадокса. Мало найти способ, как его исключить, надо убедительно обосновать предлагаемое решение. Само сомнение в каком-то шаге, ведущем к парадоксу, должно быть хорошо обосновано.
Решение об отказе от каких-то логических средств, используемых при выводе парадоксального утверждения, должно быть увязано с нашими общими соображениями относительно природы логического доказательства и другими логическими интуициями. Если этого нет, то устранение парадокса оказывается лишенным твердых и устойчивых оснований и вырождается в техническую по преимуществу задачу.
Кроме того, отказ от какого-то допущения, даже если он и обеспечивает устранение некоторого конкретного парадокса, вовсе не гарантирует автоматически устранения всех парадоксов. Это говорит о том, что за парадоксами не следует "охотиться" поодиночке. Исключение одного из них всегда должно быть настолько обосновано, чтобы появилась определенная гарантия, что этим же шагом будут устранены и другие парадоксы.
Однако надо иметь в виду, что непродуманный и неосторожный отказ от слишком многих или слишком сильных допущений может привести просто к тому, что получится хотя и не содержащая парадоксов, но существенно более слабая теория, имеющая только частный интерес.
Многообразие или примеры парадоксов
Таракан Стасик
Таракан Стасик, находясь в точке А на стене комнаты, хочет добраться до капли варенья B, которая прилипла к противоположной стене комнаты. Ползать Стасик может по любым поверхностям: и по стенам, и по потолку, и, разумеется, по полу.
Найдите кратчайший путь Стасика из А в B и длину этого пути:

Для решения нужно развернуть комнату, как картонную коробку, и соединить две точки кратчайшим путём - отрезком прямой. Развернуть комнату можно несколькими способами, но кратчайший путь при этом будет в одном случае.
На этом рисунке представлена развёртка комнаты и точки A и B в масштабе:

А на чертеже комнаты этот маршрут будет выглядеть примерно так:
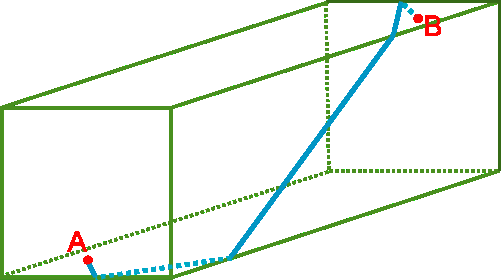
Подсчитать длину маршрута несложно: это гипотенуза треугольника с катетами 32 и 24 метра, следовательно, длина пути равна 40 метрам.
Хотя он и кажется запутанным, тем не менее, это кратчайший путь Стасика от А к B!
На уроке
Учитель нарисовал на доске четырехугольник и спросил у учеников, что это за фигура?
Иванов сказал, что это квадрат.
Петров считает, что это трапеция.
Сидоров ответил, что нарисован ромб.
Фёдоров решил, что это параллелограмм.
Оказалось, что из четырёх ответов только три были верные, а один - неверный.
Что за фигуру изобразил учитель?
Ответ: Учитель начертил квадрат, ведь он одновременно является и ромбом и параллелограммом, но не трапецией.
5 монет
Как можно разложить на столе пять монет в два ряда, причём так, чтобы в одном ряду оказалось три монеты, а в другом - четыре?
Ответ: Можно положить две монеты друг на друга, тогда получится два ряда, по четыре и три монеты:

Число π равно двум

Дано: окружность радиуса R. Кривая А (на рисунке красная) построена из двух полуокружностей радиуса R/2. Следовательно, длина кривой А равна πR. Кривая B построена из четырёх полуокружностей радиуса R/4, её длина также равна πR. Аналогично, кривая C построена из восьми полуокружностей радиуса R/8 и длина её так же составляет πR. Продолжая построение, получим последовательность кривых, составленных из полуокружностей радиуса, стремящегося к нулю, длина всех этих кривых равна πR.
Очевидно, что кривые, с увеличением числа составляющих полуокружностей и с уменьшением их радиуса, стремятся к отрезку MN, длина которого равна 2R. Таким образом, получаем:
πR = 2R, следовательно,
π = 2
А теперь - вопрос: доказано, что число π равно двум. Почему же повсеместно используется более длинное и неудобное значение 3.1415...?
Ответ: С уменьшением радиуса полуокружностей, составляющих кривую, она приближается к отрезку-диаметру MN, однако форма полуокружностей не меняется. Сколь "мелкими" они бы ни становились, их длина всё равно будет равняться πR.
Поэтому, как это ни печально, число π не равно двум. А как было бы удобно, если бы это было правдой!
Число π равно четырем
Путём простых и очевидных построений можно легко доказать, что число π равно четырём (доказательство π равно 2).
Начертим окружность с диаметром, равным единице:
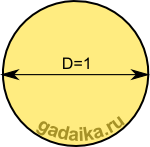
Теперь опишем квадрат вокруг этой окружности. Периметр этого квадрата будет равен четырём, ведь каждая сторона равна единице.

Теперь "отрежем" углы у квадрата, чтобы получившаяся фигура более точно повторяла окружность. Отрезать будем прямоугольные кусочки, поэтому периметр фигуры, которая раньше была квадратом, не изменится.

Повторяем "отрезание", чтобы оставшаяся от квадрата часть была похожа на круг. Кое-где можно не отрезать, а наоборот, "добавлять" прямоугольные кусочки, чтобы максимально приблизить фигуру к окружности. Периметр при этом, опять же, не меняется.

Проделав это бесконечное число раз (с каждым разом фигура приближается к окружности), получим точный контур окружности. А ведь фигура, которую мы "превратили" в круг, имеет всё тот же периметр, равный четырём! Этот периметр теперь - длина окружности, получившейся из квадрата. Диаметр этой окружности равен единице. Найдём теперь число π из определения:
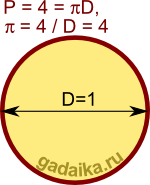
π = 4 / D = 4.
Итак, доказано: число π равно четырём. Не давайте преподавателям геометрии вводить себя в заблуждение! Хотя, с другой стороны, π равно двум, так что выбирайте на свой вкус.
Данное "доказательство" представляет собой софизм. Кажется, что фигура, которая получается из квадрата, и в самом деле будет в точности повторять круг: ведь все отрезки, из которых состоит фигура, будут находиться сколь угодно близко к окружности.
Несмотря на это, фигура кругом никогда не станет, потому что сколь малыми бы ни были её элементы, они представляют собой "угловатую" ломаную линию, периметр которой не меняется.
Это "доказательство" опирается на те же ошибочные предположения, выдвинутые в доказательстве "π равно 2".
Отъеденный торт
Студенты-первокурсники в общежитии отмечали конец первой сессии. В холодильник студенты поставили торт прямоугольной формы, с тем, чтобы вынуть его, когда дело дойдёт до утреннего чая. Велико же было их удивление, когда утром обнаружилось, что из торта неизвестными был выеден кусок прямоугольной формы.
Как теперь разделить торт на две равные части одним прямым разрезом?
Ответ: Надо разрезать торт по линии, соединяющей центр торта и центр выеденного прямоугольника.
Парадокс лжеца
Человек сказал: "То, что я сейчас утверждаю – неправда".
В самом деле, если он сказал правду, то, судя по его словам он соврал. И наоборот, если человек сказал неправду – из его слов следует, что он прав... Аналогично, беседа Платона и Сократа приводит к тому же парадоксу:
Платон: – Следующее высказывание Сократа будет ложным.
Сократ: – То, что сказал Платон, истинно.
Это утверждение нельзя ни доказать, ни опровергнуть, поэтому считается, чт оно вообще не является логическим утверждением.
Задача двух генералов
Сейчас я объясню, почему невозможно доставить сообщение получателю с абсолютной гарантией получения. Описанную ниже проблему называют "задачей двух генералов".
Две армии, которыми руководят два генерала, приготовились штурмовать город. Армии расположены так, что единственная связь между ними - путём отправки гонца с письмом. Вокруг полно вражеских патрулей, поэтому гонца могут перехватить и он не доберётся до получателя. Штурм должны начать обе армии одновременно, иначе операция обречена на провал.
Оба генерала собираются штурмовать город, но время штурма ещё не согласовано. Проблема заключается в том, чтобы надёжно обменяться сообщениями о "времени Ч" с целью утвердить время начала штурма.
Для того, чтобы согласовать время начала штурма, необходимо всего лишь обменяться сообщениями: генерал А отсылает генералу Б гонца с письмом, в котором указывает время. Б, получив сообщение, отправляет гонца обратно с подтверждением о получении сообщения. А, получив подтверждение, становится уверен в том, что Б теперь знает время начала штурма.
Однако, теперь Б не знает, получил ли А подтверждение о том, что Б получил первое послание, ведь гонца могли поймать враги. Поэтому, как только гонец от Б к А доставит подтверждение, А должен теперь отослать ещё одного гонца к Б, который сообщил бы, что письмо с подтверждением от Б к А получено. Казалось бы, этого достаточно, но нет!
Теперь А, отослав гонца с сообщением о подтверждении о получении сообщения, полученного от Б, должен как-то удостовериться, что гонец этот добрался до Б. Следовательно, Б тепер должен отправить очередного гонца к А.
Эту цепочку можно продолжать как угодно долго. На каждом этапе либо генерал А, либо Б не уверены в том, что адресат получил сообщение, поэтому гонцами придётся обмениваться вечно. Это означает, что не существует надёжного способа передать сообщение от А к Б.
На практике можно поступить так: послать не одного, а сразу нескольких гонцов по разным дорогам или тропинкам в лесу и не ждать подтверждения о получении. Тогда вероятность успешной доставки сообщения повысится до некой необходимой величины, но доставка всё же не будет абсолютно надёжной.
Лампочка
Временной парадокс с лампой — пример философской сверхзадачи. Представьте себе обычную настольную лампу, которую можно включить и выключить, нажимая на выключатель. Лампа может быть либо включена, либо выключена.
Некто начинает включать и выключать лампу по такому принципу:
Лампа включается. В течение первой минуты лампа включена, следующие полминуты лампа выключена. Следующую четверть минуты лампа опять включена, потом 1/8 минуты выключена, и так далее. Так продолжается ровно 2 минуты: лампу включают и выключают всё чаще.
Проходит две минуты с начала эксперимента и наш "некто" перестаёт щёлкать выключателем.
По истечении всего эксперимента лампа окажется либо включенной, либо выключенной, ведь других состояний у неё быть не может.
Останется ли лампа включенной, или окажется выключенной по окончании эксперимента?
Ответ: Видно, что за 2 минуты придётся нажать на выключатель бесконечное число раз, ведь каждый раз отрезок времени, оставшийся до конца эксперимента, делится на два, затем ещё на два, и так до бесконечности.
Можно пронумеровать все нажатия на выключатель. Каждое нечётное нажатие выключателя включает лампу, каждое чётное — выключает её. Значит, если после завершения эксперимента лампа оказалась выключенной, последнее число эксперимента чётное, а если оказалась включенной — последнее число нечётное.
Но поскольку понадобится сделать бесконечное число нажатий, то последнего числа не существует! А ведь лампа в конце эксперимента останется либо включенной, либо выключенной, но узнать её конечное состояние невозможно никаким способом!
Парадокс Архимеда
Парадокс Архимеда утверждает, что любое тело может плавать в объёме воды меньшем, чем объем самого тела, если средняя плотность этого тела меньше, чем плотность воды. Таким образом, массивное тело (например, корабль) может плавать в объёме воды значительно меньшем, чем объём самого тела, при условии, что вода окружает тело со всех сторон.
Этот парадокс назван в честь известного Архимеда из Сиракуз, который открыл знаменитый закон Архимеда. Согласно этому закону сила, действующая на тело, погруженное в жидкость, равна весу вытесняемого им объёма жидкости. В примере с кораблём сила Архимеда равна весу воды в объеме той части корабля, которая погружена в воду. Если вытесняющая сила больше, чем вес корабля, то он будет плавать.
Этот парадокс опирается на факт, что для силы Архимеда важен объём погружённой части плавающего тела, а не объём воды, которое это тело вытесняет.
Поезд и самоубийство
Однажды в одном городе Х произошла следующая история.
Во время движения поезда один из пассажиров выпрыгнул из вагона и разбился насмерть. Известно, что он ехал один. В купе больше никого не было в этот момент. На столе в купе был найден кусок марлевого бинта. Если бы он ехал другим видом транспорта, то скорее всего, он бы не стал самоубийцей.
Итак вопрос, почему он покончил с жизнью?
Ответ: Человек ехал домой после завершения курса лечения от слепоты. У него была марлевая повязка на глазах, защищавшая глаза от света.
В пути он не смог удержаться от соблазна снять повязку раньше времени. По трагическому стечению обстоятельств, он сделал это в тот момент, когда поезд проезжал по длинному тоннелю. В купе в это время царила полная темнота.
Ничего не увидев, человек сделал ошибочный вывод, что лечение не помогло. От отчаяния человек покончил с собой, выбросившись из окна.
Оптимальная ломаная
Как надо провести непрерывную ломаную линию из четырёх отрезков, чтобы она прошла через центры всех девяти кружков?

Ответ: Отрезки ломаной не обязательно должны начинаться и заканчиваться в кружках:

Масса и площадь шара
Сможет ли человек поднять железный шар, который вмещает столько же кубических сантиметров, сколько квадратных сантиметров содержит вся его поверхность?
Ответ: Да, сможет. Вспомним формулы нахождения площади и объёма шара.
Площадь шара: S=4 π R²
Объём шара: V = 4/3 π R³
Приравняем их и найдём радиус:
4/3 π R³ = 4 π R²
1/3 R³ = R²
1/3 R = 1
R = 3
Радиус шара может составлять 3 см, тогда его объём составит столько же кубических сантиметров, сколько квадратных сантиметров составляет площадь его поверхности.
Железный шарик радиуса 3 сантиметра поднять можно без проблем.
Кубик и ножовка
Представьте, что у вас есть деревянный кубик. Вы отпиливаете у него одну вершину. Сколько теперь вершин у такого "куба" с отпиленным углом?
Ответ: Условия задачи явно недостаточно для того, чтобы дать однозначный ответ! Если отпилить самый кончик куба, то у оставшейся части вершин станет на две больше. При этом отпиленная пирамидка будет иметь четыре вершины.
Попробуйте изменить вопрос, так: сколько вершин стало после того, как от куба отпилили одну вершину? Ответом на такой вопрос должно быть "число вершин увеличится на 6, так как на 2 вершины станет больше на самом остатке куба, плюс отпиленная часть это ещё четыре вершины".
Возможны вариации и с местом распила: если распилить куб по диагонали так, что распил пройдет через другие вершины, ответ будет другим! Главное - не ошибиться с формулировкой вопроса!
Цифры
Дано 10 цифр, расставленных по некоторому закону:
8, 2, 9, 0, 1, 5, 7, 3, 4, 6
Сможете ли вы определить, почему именно в этом порядке стоят цифры?
Ответ: Цифры упорядочены по алфавиту:
восемь, два, девять, ноль, один, пять, семь, три, четыре, шесть
Заключение
Учитывая стремительное развитие нашего мира, и всего что нас окружает, для каждого из нас необходимо знать хотя бы основы всего, что мы делаем. И неважно, чем занимаешься – делаешь покупки или создаёшь поделку, а может, даже просто играешь в модные сегодня игры – основой всего является математический расчёт. И самые незабываемые занятия, такие как телевидение, фотография, информатика, основой для них служат цифры (не зря у нас – цифровое ТВ, цифровые фотографии и даже сам разум человека, как предполагают многие ученые – закодирован, сродни компьютеру в цифровом формате.) Ну а парадоксы и математика – совместимы, и это очень интересная тема, надеюсь не только для меня, но и для вас. Моя работа доказательство этому.
Анри Пуанкаре говорил: «Если кто-либо хочет кратким и выразительным словом определить само существо математики, тот должен сказать, что это наука о бесконечности».
А закончить свою работу, я хочу следующим четверостишьем:
Пытаться понять о том, как надо жить
Вопросы задают, веками рассуждают
Но если всё нам это на цифры разложить
Историю всех стран один лишь диск вмещает.
Информационные ресурсы
Алфутова Н.Б., Устинов А.В. «Алгебра и теория чисел»
Алфутова Н.Б., Устинов А.В. «Шутки и ошибки»
www.gadaika.ru
16



























