Муниципальное бюджетное общеобразовательное учреждение
Мурыгинская средняя школа
Починковского района
Смоленской области
Проект на тему:
«Звёздчатые многогранники»
Выполнил:
ученик 10 класс
Симуров Александр
Руководитель:
учитель математики
высшей квалификационной категории
Швецова Е.В.
Мурыгино
2021
Содержание
1. Введение
2. Глава 1. Основные сведения о многогранниках
1.1. Правильные звёздчатые многогранники
1.2. Полуправильные многогранники
1.3. Звездчатые многогранники
1.3.1. Звездчатый октаэдр
1.3.2. Звёздчатые формы додекаэдра
1.3.3. Звёздчатые формы икосаэдра
1.3.4. Звездчатые кубооктаэдры
1.3.5. Звездчатые икосаэдры
1.3.6. Звездчатые икосододекаэдры
1.4. Многогранники в жизни
3. Глава 2. Создание моделей многогранников
Заключение
Список использованной литературы
Введение
Наш мир удивителен, каждый предмет имеет свою форму, строение, состав и текстуру. Изучая тему «Правильные многогранники», мы узнали от учителя о существовании таких замечательных фигур, как звездчатые многогранники. Читая энциклопедии и статьи в интернете, я узнал много нового об этих красивых фигурах. Недавно я решил своё будущее связать с архитектурой, поэтому думаю поступать в архитектурный вуз. В своих будущих проектах и исследованиях мне бы хотелось применить те знания и умения, которые я получил в ходе моей проектной деятельности.
Актуальность темы моей работы заключается в том, что учёные в наши дни изучают многогранники и составляют различные научные гипотезы, которые в будущем могут привести к различным открытиям. Данная тема актуальна, так как немногие люди знают правильные многогранники, но знание этих геометрических тел поможет в создании различных шедевров, как в архитектуре, так и в живописи и во многом другом, потому что многогранники имеют обширную область применения.
На сегодняшний день существует много работ, посвящённых звёздчатым многогранникам. Учебные пособия предлагают изготовить только правильные многогранники. Однако я решил изучить эту тему на примере нашего класса и изготовить звёздчатые многогранники с одноклассниками. Эти фигуры могут стать хорошим украшением и предметом интерьера. В этом заключается новизна моего проекта.
Цели:
познакомиться со звездчатыми многогранниками;
изучить теорию выполнения моделей звездчатых многогранников;
выполнить модели звездчатых многогранников;
подробнее узнать о применении этих фигур в архитектуре и искусстве, изучить их формы в природе.
Задачи:
найти теорию о звездчатых многогранниках;
узнать виды звёздчатых многогранников и их строение;
найти изображения звездчатых многогранников;
разобрать план выполнения моделей;
создать модели звёздчатых многогранников с одноклассниками;
изучить применение звёздчатых многогранных форм в науке и архитектуре, искусстве.
Глава 1. Основные сведения о многогранниках
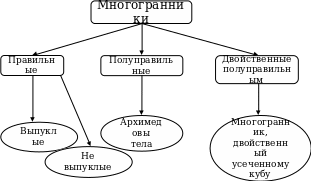
1.1. Правильные звёздчатые многогранники
На страницах современных энциклопедий и в интернете можно найти информацию о том, что правильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются одинаковые (конгруэнтные) правильные или звёздчатые многоугольники. В отличие от пяти классических правильных многогранников (платоновых тел), данные многогранники не являются выпуклыми телами.
В 1811 году Огюстен Лу Коши установил, что существуют всего четыре правильных звёздчатых тела (они называются телами Кеплера- Пуансо), которые не являются соединениями платоновых и звёздчатых тел. К ним относятся открытые в 1619 году Иоганном Кеплером малый звёздчатый додекаэдр и большой звёздчатый додекаэдр, а также большой додекаэдр и большой икосаэдр, открытые в 1809 году Луи Пуансо. Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кеплера-Пуансо.
Полуправильные звёздчатые многогранники – это звёздчатые многогранники, гранями которых являются правильные или звёздчатые многоугольники, но не обязательно одинаковые. При этом строение всех вершин должно быть одинаковым (условие однородности). Г. Коксетер, М. Лонге-Хиггинс и Дж. Миллер в 1954 году перечислили 53 таких тела и выдвинули гипотезу о полноте своего списка. Только значительно позже в 1969 году Сопову С. П. удалось доказать, что представленный ими список многогранников действительно полон. Правильные многогранники с древних времен привлекали к себе внимание ученых, строителей, архитекторов и многих других. Их поражала красота, совершенство, гармония этих многогранников. Пифагор и его ученики считали эти многогранники божественными и использовали их в своих философских сочинениях о существе мира, придавая форму правильных многогранников элементам первооснов бытия, а именно: огонь – тетраэдр (его гранями являются четыре правильных треугольника; земля – гексаэдр (куб, его гранями являются шесть квадратов); воздух – октаэдр (его гранями являются восемь правильных треугольников); вода – икосаэдр (его гранями являются двадцать правильных треугольников); вся Вселенная, по мнению древних, имела форму додекаэдра (его гранями являются двенадцать правильных пятиугольников). Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: «Тетра» четыре; «Гекса» – шесть; «Окто» – восемь; «Икоси» – двадцать; «Додека» – двенадцать; «Эдра» – грань. Подробно описал свойства правильных многогранников древнегреческий ученый Платон (427 – 347 гг. до н.э.). Именно поэтому правильные многогранники называются также телами Платона. Правильным многогранникам посвящена последняя XIII книга знаменитых «Начал» Евклида.
Иоганн Кеплер (27 декабря 1571 г. – 15 ноября 1630 г) (Приложение 1) в своей работе «Тайна мироздания», используя правильные многогранники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы. Геометрия Солнечной системы, по Кеплеру, заключалась в следующем: «Земля (имеется в виду орбита Земли) есть мера всех орбит. Вокруг нее опишем додекаэдр. Описанная вокруг додекаэдра сфера есть сфера Марса. Вокруг сферы Марса опишем тетраэдр. Описанная вокруг тетраэдра сфера есть сфера Юпитера. Вокруг сферы Юпитера опишем куб. Описанная вокруг куба сфера есть сфера Сатурна. В сферу Земли вложим икосаэдр. Вписанная в него сфера есть сфера Венеры. В сферу Венеры вложим октаэдр. Вписанная в него сфера есть сфера Меркурия». Такая модель Солнечной системы получила название «Космического кубка» Кеплера.
Вслед за Евклидом изучением пяти правильных многогранников занимался Архимед (287—212 гг. до н. э.). Убедившись в том, что нельзя построить шестой правильный многогранник, Архимед стал строить многогранники, у которых гранями являются правильные, но не одноименные многоугольники.
1.2. Полуправильные многогранники
К полуправильным многогранникам относятся правильные n-угольные призмы, все ребра которых равны, и, так называемые, антипризмы с равными ребрами, которые получаются из призм поворотом одного из оснований относительно другого.
Кроме этих двух бесконечных серий полуправильных многогранников, имеется еще 13 полуправильных многогранников, которые впервые открыл и описал Архимед.
До нас дошла работа самого ученого «О многогранниках», в которой подробно описаны и даны рисунки всех 13 многогранников, названных в честь ученого телами Архимеда.
Перечислим их: усеченный тетраэдр; усеченный куб; усеченный; октаэдр; усеченный икосаэдр; усеченный додекаэдр; кубооктаэдр; икосододекаэдр; усеченный кубооктаэдр; усеченный икосододекаэдр; ромбокубооктаэдр; ромбоикосододекаэдр; курносый куб; курносый додекаэдр.
Перечисленные тела Архимеда называются также равноугольно полуправильными многогранниками, так как они имеют равные многогранные углы.
Модели правильных и полуправильных многогранников можно склеивать из бумаги или собирать из геометрического конструктора, состоящего из многоугольников, сделанных из плотного материала с отгибающимися клапанами и резиновых колечек – основной крепежной детали конструктора, которые можно нарезать из велосипедной камеры.
Все многоугольники должны иметь равные стороны. Желательно иметь многоугольники нескольких цветов. Подбирая соответствующим образом многоугольники в качестве граней многогранника и скрепляя их резиновыми колечками, можно получать модели различных многогранников. Для того чтобы колечки лучше держались и не мешали друг другу, уголки многоугольников в конструкторе можно немного обрезать.
Многогранники, двойственные к равноугольно полуправильным многогранникам, называются равногранно полуправильными многогранниками. Они имеют равные грани и правильные многогранные углы.
Многогранниками, двойственными к призмам и антипризмам, являются бипирамиды и антибипирамиды.
Многогранники, двойственные телам Архимеда, называются телами Каталана.
1.3. Звездчатые многогранники
Кроме правильных и полуправильных многогранников, красивые формы имеют, так называемые, правильные звездчатые многогранники. Они получаются из правильных многогранников продолжением их граней или ребер. Их всего четыре. Первые два были открыты И. Кеплером, это звездчатый додекаэдр и большой звездчатый додекаэдр. Два других почти 200 лет спустя построил Л. Пуансо (1777—1859 гг.), это большой додекаэдр и большой икосаэдр. Именно поэтому правильные звездчатые многогранники называются телами Кеплера-Пуансо.
1.3.1. Звездчатый октаэдр
С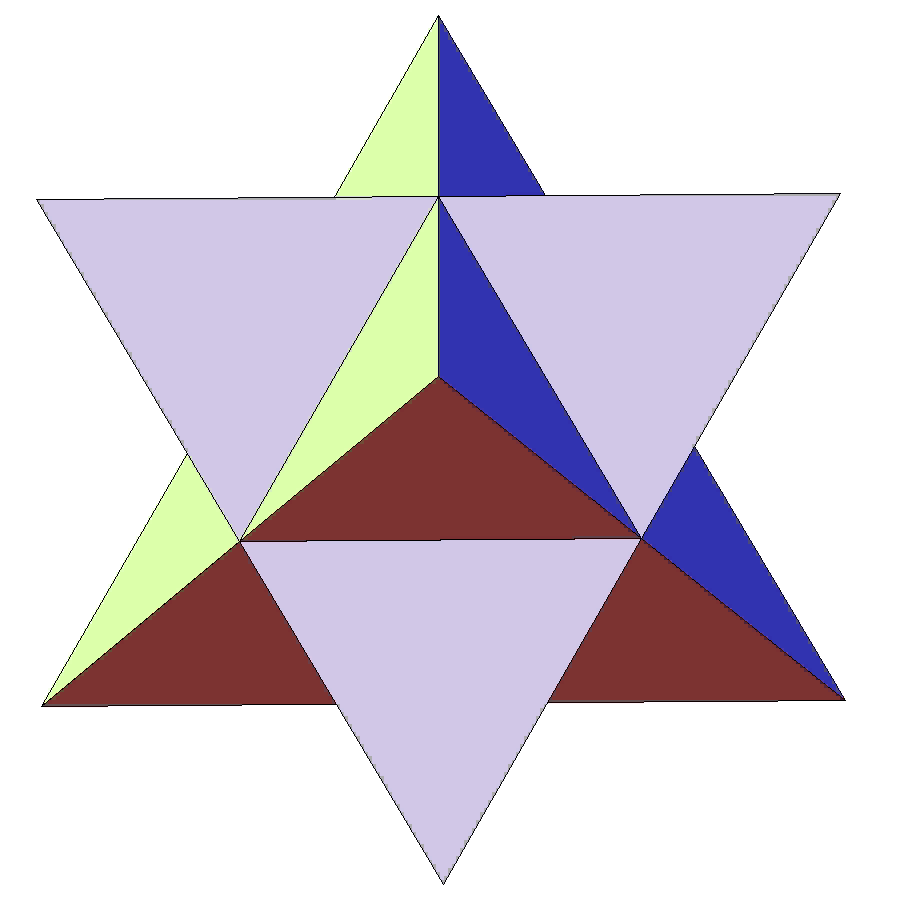 уществует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula – звезда восьмиугольная. Отсюда эта форма имеет и второе название «stella octangula Кеплера». По сути она является соединением двух тетраэдров.
уществует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula – звезда восьмиугольная. Отсюда эта форма имеет и второе название «stella octangula Кеплера». По сути она является соединением двух тетраэдров.
Октаэдр один из пяти выпуклых правильных многогранников, так называемых Платоновых тел.
1.3.2. Звёздчатые формы додекаэдра
| Малый звездчатый додекаэдр | Большой додекаэдр | Большой звёздчатый додекаэдр |
| 
| 
| 
|
Додекаэдр имеет три звёздчатые формы: малый звездчатый додекаэдр, большой додекаэдр, большой звёздчатый додекаэдр. Первые две из них были открыты Кеплером (1619), третья Пуансо (1809).
Все три звёздчатые формы додекаэдра, вместе с большим икосаэдром образуют семейство тел Кеплера-Пуансо, то есть правильных невыпуклых (звёздчатых) многогранников.
У большого додекаэдра гранями являются пятиугольники, которые, сходятся по пять в каждой из вершин. У малого звёздчатого и большого звёздчатого додекаэдров грани – пятиконечные звёзды (пентаграммы), которые в первом случае сходятся по 5, а во втором по 3.
Вершины большого звёздчатого додекаэдра совпадают с вершинами описанного додекаэдра. У каждой вершины соединяются три грани.
Малый звездчатый додекаэдр
Малый звёздчатый додекаэдр – тело Кеплера- Пуансо, с символом Шлефли. Многограннику дал имя Артур Кэли. Многогранник является одним из четырёх невыпуклых правильных многогранников. Он состоит из 12 граней в виде пентаграмм (пятиконечные звёзды) с пятью пентаграммами, сходящимися в каждой вершине.
Большой додекаэдр
Большой додекаэдр—это тело Кеплера- Пуансо, с символом Шлефли и диаграммой и диаграммой Коксетера-Дынкина. Это один из четырёх невыпуклых правильных многогранников. Он состоит из 12 пятиугольных граней (шесть пар параллельных пятиугольников), с пятью пятиугольниками в каждой вершине, пересекающих друг друга и создающих рисунок пентаграммы.
Этот многогранник получается при продолжении граней додекаэдра. Его можно также получить из икосаэдра, вырезанием из его граней правильных треугольных пирамид.
Большой звёздчатый додекаэдр
Большой звёздчатый додекаэдр – это тело Кеплера-Пуансо, с символом Шлефли. Многогранник является одним из четырёх невыпуклых правильных многогранников. Он состоит из 12 пересекающихся граней в виде пентаграмм с тремя пентаграммами, сходящимися в каждой вершине.
1.3.3. Звёздчатые формы икосаэдра
Икосаэдр — это многогранник с 20 гранями. Существует бесконечно много непохожих икосаэдров, некоторые из которых имеют больше симметрий, другие меньше. Наиболее известен (выпуклый, незвёздчатый) правильный икосаэдр – один из правильных многогранников, гранями которого являются 20 правильных треугольников
Икосаэдр имеет 59 звёздчатых форм, из которых 32 обладают полной, а 27 неполной икосаэдральной симметрией, что было доказано Кокстером совместно с Дювалем, Флэзером и Петри c применением правил ограничения, установленных Дж. Миллером. Одна из этих звёздчатых форм (20-я, мод. 41 по Веннинджеру), называемая большим икосаэдром, является одним из четырёх правильных звёздчатых многогранников Кеплера—Пуансо. Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.
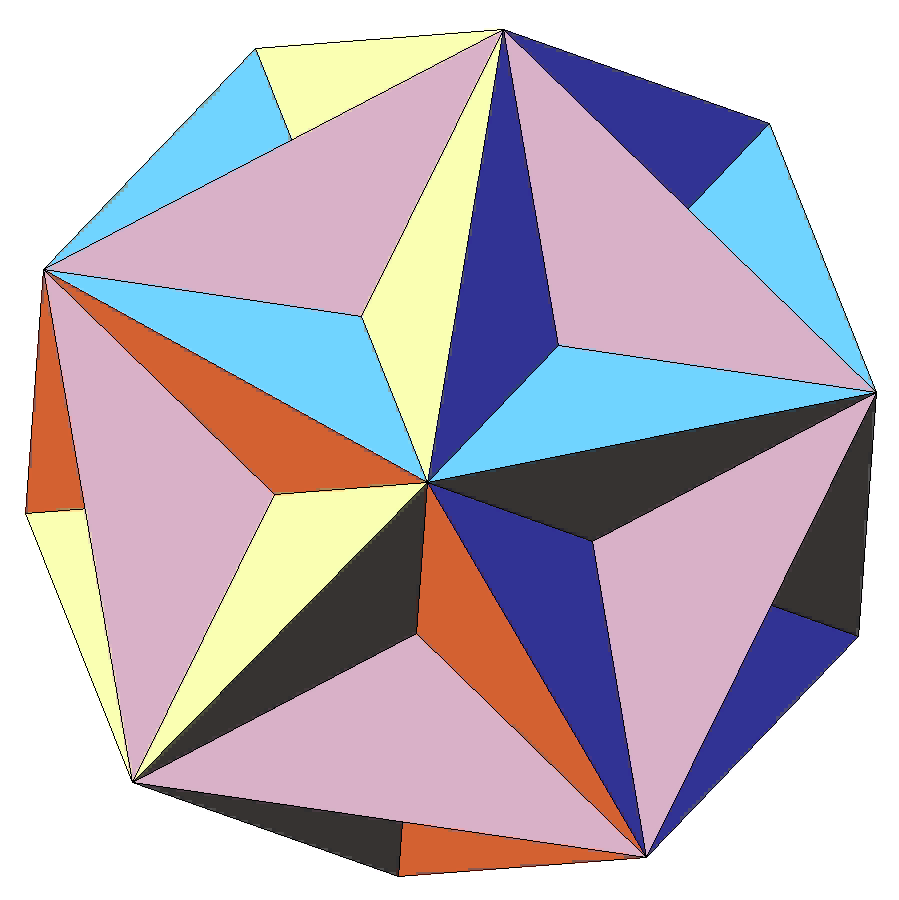
Икосаэдр имеет двадцать граней. Если каждую из них продолжить неограниченно, то тело будет окружено большим многообразием отсеков — частей пространства, ограниченных плоскостями граней. Все звёздчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства 20+30+60+20+60+120+ 12+30+60+60 отсеков десяти различных форм и размеров. Большой икосаэдр (рисунок 1) состоит из всех этих кусков, за исключением последних шестидесяти.
Рисунок 1. Большой икосаэдр
П олучается продолжением граней икосаэдра. Его можно также получить из малого звездчатого додекаэдра вырезанием из его граней треугольных пирамид.
олучается продолжением граней икосаэдра. Его можно также получить из малого звездчатого додекаэдра вырезанием из его граней треугольных пирамид.
1.3.4. Звездчатые кубооктаэдры
Помимо правильных звездчатых многогранников (тел Кеплера-Пуансо) имеется более сотни различных звездчатых форм многогранников.
Кубооктаэдр – полуправильный многогранник, состоящий из 14 граней (8 правильных треугольников и 6 квадратов). В кубооктаэдре 12 одинаковых вершин, в которых сходятся два треугольника и два квадрата, а также 24 одинаковых ребра, каждое из которых разделяет треугольник и квадрат.
Кубооктаэдр имеет 4 звёздчатые формы. Первая из них является соединением куба и октаэдра.
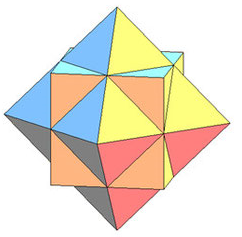
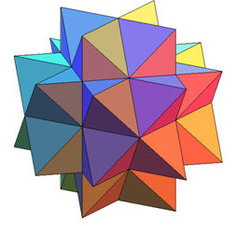
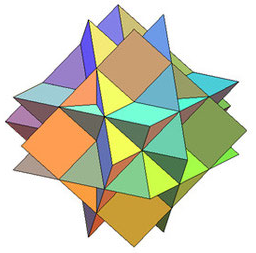

1.3.5. Звездчатые икосаэдры
На рисунке показаны некоторые звездчатые формы икосаэдра. Всего их 59.
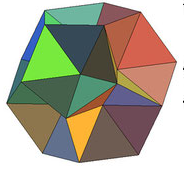





1.3.6. Звездчатые икосододекаэдры
На рисунке показаны некоторые звездчатые формы икосододекаэдра. Всего их 19.
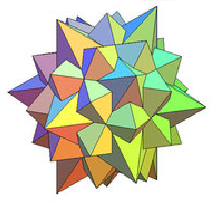
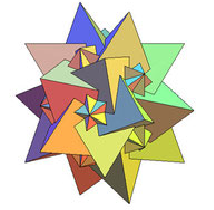

1.4. Многогранники в жизни
Мир наш исполнен симметрии. С древнейших времен с ней связаны наши представления о красоте. Наверное, этим объясняется непреходящий интерес человека к удивительным символам симметрии, привлекавшим внимание множества выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши.
1.4.1. Звездчатые многогранники в архитектуре
Пирамиды Гизы:

Александрийский маяк:

Модель звёздчатого многогранника в жизни:

Национальная Белорусская библиотека:

Здание в Новосибирске – фантастический четырёхэтажный шар:

Памятный знак военному аэродрому "Гражданка" в Санкт-Петербурге:

Спасская башня Московского Кремля:


Мечеть Кул-Шариф в Казани:

1.4.2. Звездчатые многогранники в искусстве
Сальвадор Дали ‘’Тайная вечеря’’

Мауриц Корнелис Эшер «Stars»

Мозайчатые фрески, созданные в эпоху Возрождения:


1.4.3. Звездчатые многогранники в природе
|  Алмаз |  Пирит |  Поваренная соль |
|  Шпинель |  Гранат |  Датолит |
|  Фтор |  Аквамарин |  Топаз |
Снежинки – это звёздчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

Вирусы имеют различные размеры и форму. Чаще всего сферическая по форме внешняя оболочка обладает кубическим (икосаэдрическим) типом симметрии. В этом случае капсомеры организуются в икосаэдр. Исследователи рассмотрели крупные вирусные оболочки, содержащие более 60 белков в рамках не привычной развертки икосаэдра, а развертки додекаэдра. Как оказалось, локальный порядок белков (закономерность расположения соседних молекул) в оболочках больших вирусов хорошо совместимым с додекаэдрической разверткой.
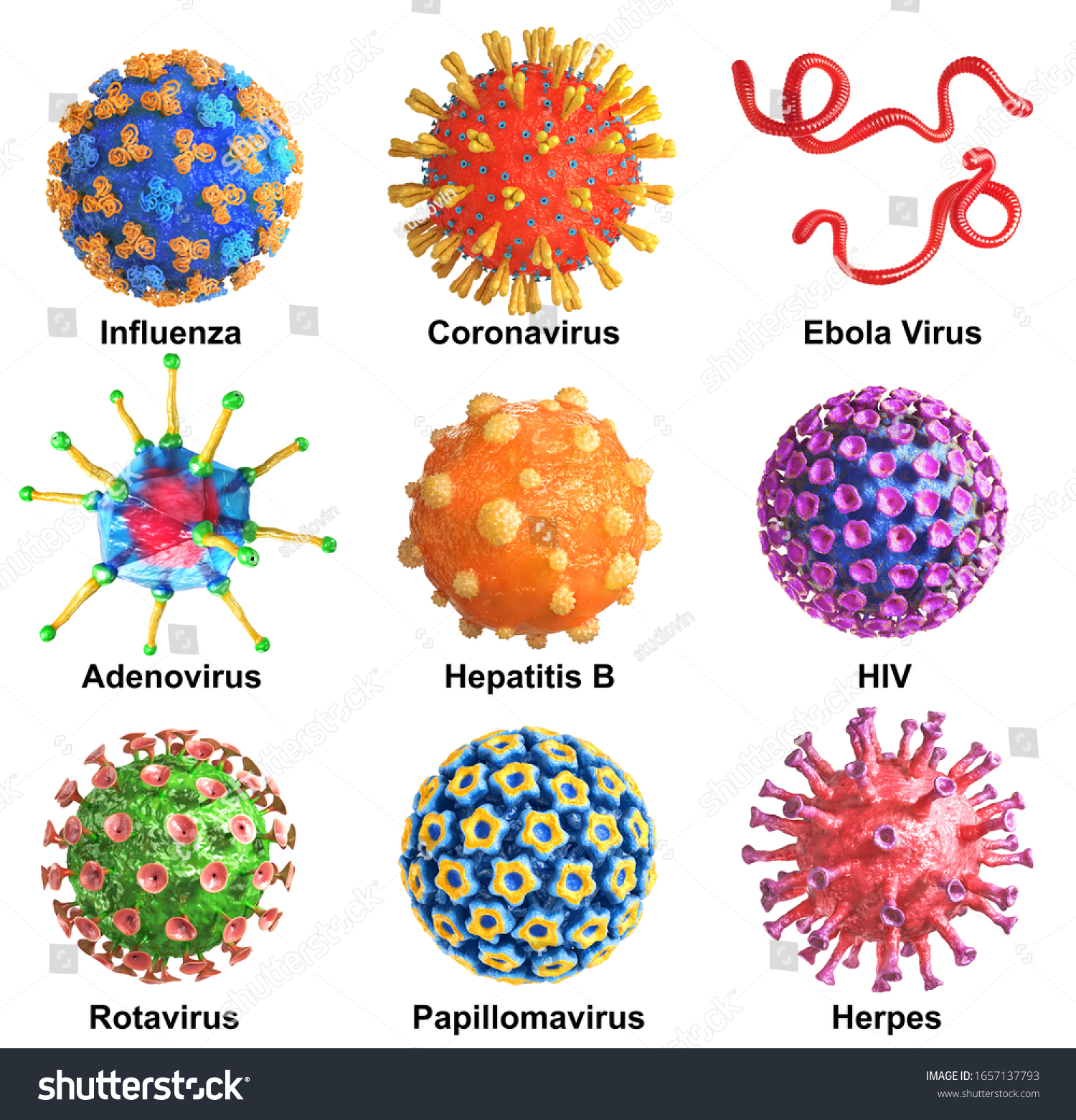
Выводы
Изучая теорию о правильных многогранниках, я узнал, что существует большое множество различных звёздчатых многогранников. – удивительных геометрических тел, которые привлекают своими оригинальными формами. Но сведений об этих геометрических телах нет в учебниках.
Мир наш исполнен симметрии. С древнейших времен с ней связаны наши представления о красоте. Наверное, этим объясняется непреходящий интерес человека к удивительным символам симметрии, привлекавшим внимание множества выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши.
Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа, например снежинки - это тоже звездчатые многогранники.
Этим проектом хотелось бы расширить представления о мире многогранников и доказать, что многогранники - слагаемые прекрасного.
Глава 2. Создание моделей многогранников
Я познакомил одноклассников с изученным материалом. Это вызвало живой интерес к данной теме. (Фото)
Мы рассмотрели все имеющиеся у меня модели. И я предложил изготовить, используя шаблоны звёздчатый икосаэдр.
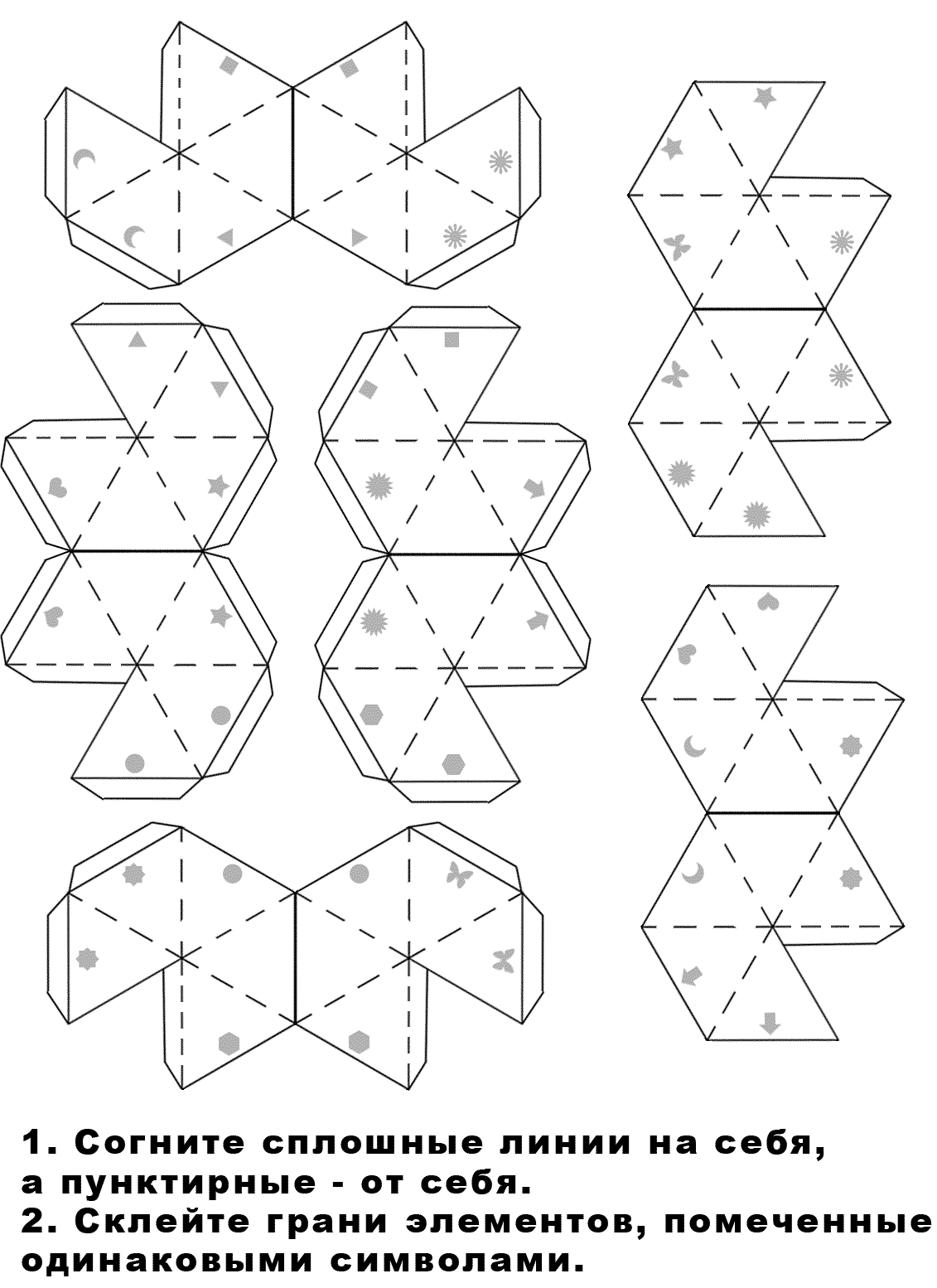
Чтобы самому делать красивые формы звёздчатых многогранников, сначала необходимо сделать развертку. Для этого нужно мысленно развернуть фигуру, чтобы ее можно было изобразить на плоском листе бумаги.
Развертку можно начертить с помощью циркуля, линейки и транспортира. Обязательно нужно предусмотреть клапана для склейки.
Затем по линейке продавить линии сгиба. Это надо сделать обязательно, иначе бумага согнется неровно. Вырезать заготовки, согнуть и склеить их.
Можно самому придумывать разные формы разверток и смотреть какие получаются фигуры.
Но если развёртка занимает весь лист формата А4, многогранник получается маленького размера. Поэтому удобнее использовать шаблоны – части развёртки.
И мы занялись изготовлением звёздчатого икосаэдра. (Фото)
Выводы
Мой проект получилось удачно реализовать. Было трудно предугадать, как этому проекту отнесутся одноклассники, но им понравилась идея и они с удовольствием приняли участие в изготовлении звёздчатого икосаэдра.
Заключение
Я узнал, что существует большое множество различных звёздчатых многогранников. Собрал информацию по данной теме, познакомился с новыми понятиями, узнал о его звёздчатых формах и изготовил модели многогранников.
Я считаю, что полезно изучать многогранники, так как им можно найти применение:
Это могут быть просто красивые игрушки. Их можно повесить на елку!
Но есть серьезные применения многогранников. Например, наука кристаллография изучает строение различных веществ и подобные модели могут использоваться для изучения кристаллов.
И в нашей детской жизни тоже встречаются многогранники. Мы играем в футбол надутым многогранником! Это фигура, состоящая из пяти- и шестиугольников – усеченный икосаэдр.
Исходя из всего выше изложенного, я считаю, что достиг поставленной цели, а также выполнил все задачи. Считаю свою работу интересной, полезной и содержательной. При работе над проектом, я получил бесценный опыт: узнать что-то новое, ранее незнакомое. Я получил огромное удовольствие от проделанной мною работы. Моя работа может быть использованы на уроках геометрии, на различных конкурсах и как иллюстративный материал, может помочь расширить знания ребят по теме «Многогранники».
Список использованной литературы
1. Смирнова И. М., Смирнов В. А. Правильные, полуправильные и звездчатые многогранники. –– М.: МЦНМО, 2010.
2. Гончар В.В., Гончар Д.Р. . Модели многогранников. –– М.: «Школьные технологии», 2019.
3. Вернер А. Л., Васильева М. Н., Голокова (Данилова) О. Г. Геометрия правильных звёздчатых многогранников: учебное пособие. –– Санкт-Петрбург: « Российский государственный педагогический университет им. А. И. Герцена»., 2018
Интернет-источники
https://my-1-2.jimdofree.com/звёздчатые-многогранники/
http://mgk.olimpiada.ru/media/work/10632/развёртки_многогранников.pdf








 уществует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula – звезда восьмиугольная. Отсюда эта форма имеет и второе название «stella octangula Кеплера». По сути она является соединением двух тетраэдров.
уществует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula – звезда восьмиугольная. Отсюда эта форма имеет и второе название «stella octangula Кеплера». По сути она является соединением двух тетраэдров. 


 олучается продолжением граней икосаэдра. Его можно также получить из малого звездчатого додекаэдра вырезанием из его граней треугольных пирамид.
олучается продолжением граней икосаэдра. Его можно также получить из малого звездчатого додекаэдра вырезанием из его граней треугольных пирамид.














































