Проектная работа по математике

3

Министерство образования республики Дагестан

Управление образования Карабудахкентского района

МБОУ «Манаскентская средняя общеобразовательная школа»

Республиканская научно – практическая конференция молодых исследователей «Шаг в будущее»

Секция: математика

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

на тему: Практическое применение теоремы Пифагора

Работу выполнила Османова Юлдуз Шамиловна

Россия, Республика Дагестан,

МБОУ «Манаскентская средняя общеобразовательная школа»

9 класс

Научный руководитель:

Османова Лимуният Магомедаминовна

Россия, Дагестан, Махачкала

МБОУ «Манаскентская средняя общеобразовательная школа», учитель математики

2019г

СОДЕРЖАНИЕ

Введение

Основная часть:

1. Биография Пифагора.

2. О теореме Пифагора и способах ее доказательства

3. Задачи по теореме Пифагора

4. Применение теоремы Пифагора

5. Практическое применение.

Заключение.

Список использованной литературы.

Тема «Практическое применение теоремы Пифагора»»

Османова Юлдуз Шамиловна

Россия, Республика Дагестан,

МБОУ «Манаскентская средняя общеобразовательная школа, 9 класс

краткая аннотация:

исследовательская работа на тему «Практическое применение Теоремы Пифагора» состоит из введения, основной части, заключения и списка использованной литературы.

В введении раскрывается понятийный аппарат, дальше рассказывается краткая биография Пифагора, о его теореме и его некоторых доказательствах. Цель проекта состоит в том, чтобы показать значение теоремы Пифагора в развитии науки и практической деятельности человека.

Дальше о практическом применении этой теоремы. Затем в заключении делаются выводы.

Тема «Практическое применение теоремы Пифагора»»

Османова Юлдуз Шамиловна

Россия, Республика Дагестан,

МБОУ «Манаскентская средняя общеобразовательная школа, 9 класс

Введение

В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики.

Впервые о теореме Пифагора я узнала на уроках геометрии. Задачи на эту тему давались мне очень легко. В самом деле, теорема Пифагора проста, но не очевидна. Теорема имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.) свидетельствует о гигантском числе ее конкретных реализаций, поэтому эта тема и стала основой для моего исследования. Больше всего меня заинтересовал вопрос: каким образом теорему Пифагора можно использовать в практической деятельности человека? 

Цель моей работы состоит в том, чтобы показать значение теоремы Пифагора в развитии науки и практической деятельности человека.

Для достижения поставленной цели я поставила перед собой следующие задачи:

1. Узнать больше информации, мифов, легенд о Пифагоре и его теореме.

2. Ознакомится с различными способами доказательства теоремы Пифагора.

3. Рассмотреть применение теоремы Пифагора при решении задач.

4. Исследовать практическое применение теоремы.

Гипотеза:

С помощью теоремы Пифагора можно решать не только математические задачи, но и использовать на практике.

Объект исследования: теорема Пифагора

Предмет исследования: практическое применение теоремы в современной науке и повседневной деятельности человека.

Методы исследования:

1. Анализ различных источников литературы

2. Систематизация и обобщение данных.

Новизна. В школьном курсе геометрии с помощью теоремы Пифагора решаются только математические задачи. К сожалению, вопрос о практическом применении теоремы Пифагора практически не рассматривается.

1. Биография Пифагора

О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос. Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. По легенде, отец его, Мнесарх, обратился к Пифии по поводу одной важной для него поездки. Он получил ответ, что поездка будет удачной, а его жена родит дитя, которое будет выделяться среди всех когда-либо живших красотой и мудростью и принесет человеческому роду величайшую пользу на все времена. Мнесарх после предсказания дал своей жене новое имя – Пифаида, а новорожденному – Пифагор.

Отец дал ему хорошее образование, обучая его у самых знаменитых учителей того времени. Многие считали, что он сын бога Аполлона. После смерти отца Пифагор отправляется в Милет, где учителями его были Ферекид, Анаксимандр и Фалес. У Ферекида Пифагор получает знания основ музыки и живописи.

Пифагор тайно бежит с острова, решив продолжить образование в Египте, этой своеобразной для древних эллинов научной Мекке. Путь был далек и опасен, а все дороги вели через Милет, и здесь юный Пифагор внимательно слушает лекции Фалеса, основателя первой философской школы, тогда уже восьмидесятилетнего старца, и его более молодого коллегу и ученика Анаксимандра, выдающегося географа и астронома. Много важных знаний приобрел Пифагор за время пребывания в Милетской школе, но Фалес советует ему за знаниями продолжить путь в Египет.

Перед Египтом Пифагор на некоторое время останавливается в Финикии, где, по преданию, учится у знаменитых сидонских жрецов. Пока Пифагор был в Финикии, Поликрат не только прощает беглеца, но и пишет письмо для Амазиса - фараона Египта.

Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги – в образе полу-людей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен.

В Египте проведет он 22 года. Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С большим трудом ему удалось преодолеть эту преграду. Но жизнь его вдруг резко меняется. Скончался фараон Амазис, а его преемник по трону не выплатил ежегодную дань Камбизу, персидскому царю, что послужило поводом для войны. Персы не пощадили даже священные храмы, подверглись гонениям и жрецы, их убивали или брали в плен. Пленен был и Пифагор.

В плену в Вавилоне Пифагор встречается с персидскими магами, знакомится с учением халдейских мудрецов, со знаниями, накопленными восточными народами за многие века: астрономией, медициной и арифметикой. Изучает восточные религии. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Все это способствует тому, что он сделался одним из самых образованных людей своего времени. Приобщившись к математике, он создает из нее центр своей философской системы. Наиболее поразительными были успехи алгебры. Двенадцать лет пробыл в плену Пифагор, пока его не освободил персидский царь Дарий Гистасп, прослышавший о знаменитом греке. Пифагору уже шестьдесят, и он решает вернуться на родину, чтобы приобщить к накопленным знаниям свой народ.

Жизнь на Самосе изменилась - бурно развивались строительство и торговля. После возвращения домой Пифагор попытался создать на родине свою школу. Школа вызвала недовольство жителей острова, и Пифагору пришлось покинуть родину.

Он переселяется в южную Италию - колонию Греции – Кротон. В Кротоне Пифагор основывает школу - пифагорейский союз, просуществовавший около двух веков и ставший центром духовной и общественной жизни. Желание людей послушать философа было столь велико, что даже девушки и женщины нарушали закон, запрещавший им присутствовать на собраниях. Одна из них, Феано, становится женой Пифагора. У них рождается трое детей (два сына и дочь), в будущем последователи отца.

Свою школу Пифагор создает как тайную организацию со строго ограниченным числом учеников из аристократии, и попасть в нее было не просто. Со временем Пифагор прекращает выступления в храмах и на улицах, а учит уже в своем доме. Система обучения жаждущих знаниями сложная и многолетняя. В этот период проверялось их терпение, скромность. Одна из особенностей школы - почти священное почитание учителя. Только тех, кто прошел многие ступени знаний, Пифагор называет ближайшим учеником и допускает во двор своего дома, где они и ведут беседу. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.

Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев.

Учитель, прежде всего, учил своих учеников молчанию. «Первое упражнение будущего мудреца состояло у Пифагора в том, чтобы до конца смирить свой язык, и слова, те самые слова, что поэты называют летучими, заключить, ощипав перья, за белой стеной зубов. Иначе говоря, вот к чему сводились начатки мудрости: научиться размышлять, разучиться болтать», - пишет Апулей во «Флоридах», подтверждая, что и ему это чувство меры доставило «столько же похвал за своевременное безмолвие, сколько одобрений за уместные речи».

В "правилах" воспитания, основанных на идее о бессмертии души, обязательными были: преклонение перед богами, почитание родителей, воспитание дружбы, смелости, уважения к старшим. Пифагору приписываются "Золотые стихи" и "Символы".

Пифагорейская школа положила начало математическим наукам. Числа понимались как суть всего существующего, им придавался мистический смысл. Основу пифагорейской математики составляет учение о декаде: 1+2+3+4=10. Эти четыре числа описывают все процессы, происходящие в мире. Знаменитая декада повлияла через пифагорейцев на Платона, придававшего особое значение четырем материальным элементам: земле, воздуху, огню и воде.

Что же касается числа 36, то оно производило сильное впечатление на пифагорейцев своими качествами: с одной стороны, оно представляет сумму кубов трех первых чисел натурального ряда (1³+2³+3³), а с другой – является суммой первых четырех четных и первых четырех нечетных чисел:

(2+4+6+8) + (1+3+5+7) = 36.

Весь мир, по мнению пифагорейцев, был построен на первых четырех нечетных и на первых четырех четных числах, а потому самой страшной клятвой у них считалась клятва числом 36.

Согласно преданию, ученик Пифагора Гиппас Месапонтский, раскрывший эту тайну, был "наказан" богами и погиб во время кораблекрушения.

2.О теореме Пифагора и способах ее доказательства

Теорема Пифагора-это одна из самых известных геометрических теорем древности. Ее и сейчас знают практически все, кто когда-либо изучал планиметрию. Мне кажется, что если мы хотим дать знать внеземным цивилизациям о существовании разумной жизни на Земле, то следует посылать в космос изображение Пифагоровой фигуры.

Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством для построения прямых углов при планировке земельных участков и сооружений зданий. Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы получить прямой угол. Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике. В самом древнем дошедшем до нас китайском математико-астрономическом сочинении «Чжоу-би», написанном примерно за 600 лет до Пифагора, среди других предложений, относящихся к прямоугольному треугольнику, содержится и теорема Пифагора. Еще раньше эта теорема была известна индусам. Таким образом, Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым из области практики в область науки. Некоторыми историками математики предполагается, что все же доказательство Пифагора было не принципиальным, а лишь проверкой этого свойства на ряде частных видов треугольников, начиная с равнобедренного прямоугольного треугольника.

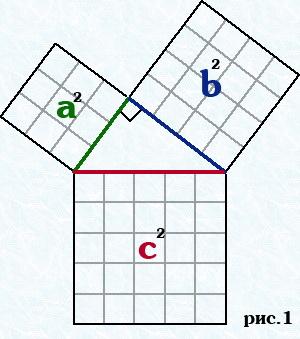
Рис. 1. Геометрическая иллюстрация к теореме Пифагора

С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен, но стремление к преумножению их числа сохранилось.

Доказательства, основанные на использовании понятия равновеликости фигур

На рис. 2 изображено два равных квадрата. Длина сторон каждого квадрата равна a + b. Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами a, b, то останутся равные площади, т. е. c² = a² + b². Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «смотри!» Вполне возможно, что такое же доказательство предложил и Пифагор.

Рис.2. Доказательство через равновеликость

Доказательство теоремы с помощью разбиения

1)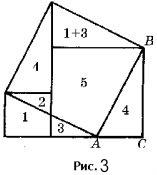 На основе доказательства ан-Найризия выполнено и другое разложение квадратов на попарно равные фигуры (рис. 3, здесь ABC – прямоугольный треугольник с прямым углом C).

Рис. 3. Доказательство ан-Найризия

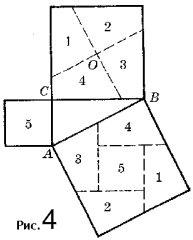
2)Еще одно доказательство методом разложения квадратов на равные части, называемое «колесом с лопастями», приведено на рис. 4. Здесь: ABC– прямоугольный треугольник с прямым углом C; O – центр квадрата, построенного на большом катете; пунктирные прямые, проходящие через точку O, перпендикулярны или параллельны гипотенузе.

Р ис. 4. «Колесо и лопасти»

Это разложение квадратов интересно тем, что его попарно равные четырехугольники могут быть отображены друг на друга параллельным переносом. Может быть предложено много и других доказательств теоремы Пифагора с помощью разложения квадратов на фигуры.

Алгебраический метод доказательства

1) Рис. 5 иллюстрирует доказательство великого индийского математика Бхаскари (знаменитого автора Лилавати, XII в.). Рисунок сопровождало лишь одно слово: СМОТРИ! Среди доказательств теоремы Пифагора алгебраическим методом первое место (возможно, самое др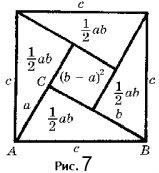 евнее) занимает доказательство, использующее подобие.

Рис. 5. Алгебраический способ

3. Задачи по теореме Пифагора

А) Задача из учебника «Арифметика» Леонтия Магницкого

« Случится некому человеку к стене лестницу прибрать, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».

Решение: ВС²=АВ²-АС²; ВС²=15625-13689=44 стоп.

Ответ: ВС=44 стоп.

Б)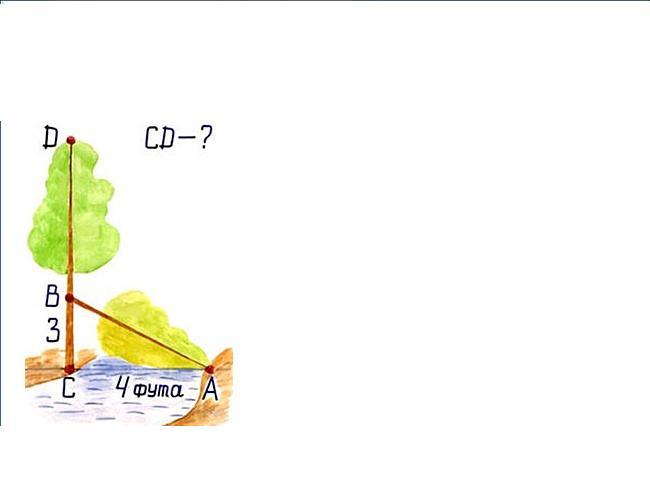 Задача Бхаскари

«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?»

Решение: По теореме Пифагора АВ²= ВС²+АС² ; 9+16=25, АВ=5 Футов; СD=3+5=8 футов.

Ответ: высота тополя 8 футов. Рис. 6. Задача Бхаскари

В) Метрополитен

Эскалатор метрополитена имеет 17 ступенек от пола наземного вестибюля до пола подземной станции. Ширина ступенек 40 см, высота 20 см. Определите а) длину лестницы, б) глубину станции по вертикали.

Решение.

а) Пусть АВ – длина лестницы из 17 ступенек.

Из  АКD по теореме Пифагора

АD =  (см),

АВ = 45 • 17 = 765 (см) = 7, 65 (м).

б) ВС = 40 • 17 = 680 (см).

Из  АСВ по теореме Пифагора

АС = (см) = 3,5 (м). Ответ: длина лестницы 7, 65 м, глубина станции 3,5 м.

Занимательная страница. Помогла теорема Пифагора

Этот эпизод взят из реальной следственной практики. Получив сообщение о краже, следователь выехал на место происшествия. Заявитель утверждал, что преступник проник в помещение, где хранились ценности, через окно. Осмотр показал, что подоконник находится на расстоянии 124 см от земли. Поверхность земли на расстоянии 180 см от стены здания покрыта густой порослью; не имевшей никаких следов повреждений. Возникло, предположение, что преступник, проникая в помещение через окно, каким-то образом преодолел расстояние между наружным краем поросли и подоконником. Оно было с применением теоремы Пифагора:

X=√124²+180²=√47776≈219 (см).

Очевидно, что преодолеть такое расстояние без какого-либо технического средства, например лестницы, невозможно. Поиски этого средства в рассматриваемом случае не увенчались успехом.

С учётом указанного обстоятельства и некоторых других данных следователь выдвинул версию об инсценировке кражи, которая входе дальнейшего расследования подтвердилась. Так школьная геометрия помогла расследованию (статья из журнала «Математика в школе», №5, 1995 г.).

4.Применение теоремы Пифагора

Теорема Пифагора издавна применялась в разных областях науки и техники, в практической жизни. Область применения теоремы достаточно обширна. Применяется в литературе, мобильной связи, архитектуре, а также в астрономии.

Теорема Пифагора была первым утверждением, связавшим длины сторон треугольников. Потом узнали, как находить длины сторон и углы остроугольных и тупоугольных треугольников. Воз­никла целая наука тригонометрия («тригон» - по-гречески означа­ет «треугольник»). Эта наука нашла применение в землемерии. Но еще раньше с ее помощью научились измерять вообра­жаемые треугольники на небе, вершинами которых были звезды. Сейчас тригонометрию применяют даже для измерения расстояний между космическими кораблями. О теореме Пифагора писали в своих произведениях писатели Плутарх, инженер Витрувий, греческий ученый Диоген, математик Прокл. Не всякое математическое положение удостаивается такого внимания поэтов и писателей.

В конце 19 века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. Вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать, но очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Использование теоремы Пифагора в Древнем Египте

Др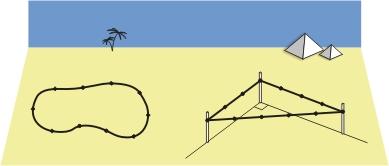 евнегреческие авторы писали о существовании в Египте особого метода для построения прямого угла на местности: этому служила кольцевая веревка, на которой были отмечены 12 узелков на равных расстояниях. Если натянуть данную веревку, образовав треугольник со сторонами, пропорциональными 3, 4 и 5, то этот треугольник будет прямоугольным: в самом деле, его стороны удовлетворяют теореме Пифагора (3² + 4² = 5²). Рис. 7. Египетский треугольник

Прямоугольные треугольники с целочисленными сторонами до сих пор иногда называются египетскими треугольниками. В то же время из сохранившихся древнеегипетских папирусов математического содержания невозможно извлечь никаких свидетельств о знакомстве с теоремой Пифагора, даже в ее частном случае. Вполне возможно, что египтяне знали только об одном целочисленном прямоугольном треугольнике, и знали о нем не раньше середины I тысячелетия до н. э.[10]

Использование теоремы Пифагора в Вавилоне

В отличие от египтян, древние вавилоняне еще в середине II тысячелетия до н. э. хорошо знали, что сумма квадратов катетов равна квадрату гипотенузы. Сохранилась таблица, из которой ясно, что вавилонянам были известны многие «пифагоровы тройки» целых чисел, удовлетворяющих равенству x² + y² = z², в том числе совсем нетривиальные (например, 72, 65, 97 или 3456, 3367, 4825). К сожалению, мы ничего не знаем о том, каким методом были найдены эти числа. Сохранились и некоторые задачи, при решении которых надо воспользоваться этой теоремой: например, требовалось определить длину шеста, который вначале вертикально прислонен к стене, а затем наклоняется так, что его верхний конец опускается на три локтя, а нижний отходит от стены на 6 локтей.[10]

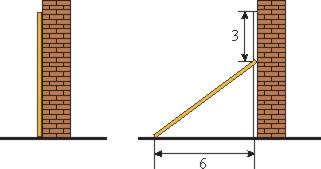
Рис. 8. Задача о шесте. Вавилон

Применение теоремы Пифагора в других отраслях

1. Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Гроза и ее непременный атрибут молния – атмосферное явление, таящее в себе достаточно большую опасность. Достаточно сказать, что в год в мире от удара молнии гибнет более 3000 человек (что гораздо больше числа погибших в авиакатастрофах), а материальный ущерб исчисляется миллиардами долларов. Я считаю, что возведение молниеотводов очень актуально, т.к. природные катаклизмы не обходят стороной и нас.

Пример: Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.

Ре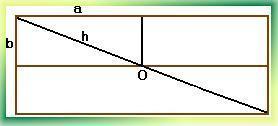 шение:

      По теореме Пифагора h²≥ a²+b², значит h≥(a²+b²)1/2.

Рис. 9. Расчеты длины молниеотвода

1. Мобильная связь. В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора.

Пример: Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)

Ре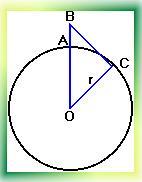 шение:

      Пусть AB= x, BC=R=200 км, OC= r =6380 км.

OB=OA+AB OB=r + x.

Используя теорему Пифагора, получим Ответ: 2,3 км.

Рис. 10. Расчеты высоты антенны

5.Практическое применение

Каждое лето я провожу в селе у бабушки. В этом году моя мама, дядя и бабушка решили построить летнюю кухню.

При этом в семье возник спор: бабушка хочет, чтобы крыша летней кухни была высотой 1м, ей кажется, что такая крыша будет выглядеть красиво.

Дядя считает, что крыша должна быть выше 2 м, т.к. с нее лучше будет скатываться снег и наледь зимой, но при этом придется наращивать стропила.

Решение данной задачи я решила возложить на свои плечи и рассчитать, какой должна быть высота крыши, чтобы конструкция была устойчивой, хватило строительного материала, и мои родственники были довольны.

Решение: размеры летней кухни 3,0 х 3,0 м, длина стропил 2,5 м.

Высота крыши вычисляется по теореме Пифагора: гипотенуза равна 2,5 м, катет 1,5 м. Второй катет равен 2м. (рис. 11)

Та ким образом, не правы ни дядя ни бабушка. И оптимально полученная высота крыши должна равняться 2 м.

Вот так теорема Пифагора помогла мне разрешить спор между родственниками.

Рис. 11. Схема летней кухни

Заключение

В заключении можно сделать вывод, что теорема Пифагора - одна из самых главных теорем геометрии потому, что с её помощью можно доказать много других теорем и решить множество задач. Теорема применяется в геометрии на каждом шагу. Всего известно около 500 различных доказательств теоремы Пифагора. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора продолжает оставаться живительным источником красоты, совершенства и творчества для новых и новых поколений.

Несмотря на то что, суть теоремы проста и изящна, но было бы ошибкой думать, что в плане её содержания не осталось места для каких-то новых исследований.

К сожалению, невозможно привести все или даже самые красивые доказательства теоремы, однако хочется надеяться, что приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к теореме Пифагора.

В результате решения поставленных задач я пришла к выводу, что выдвинутая мною гипотеза нашла подтверждение. Да, действительно, с помощью теоремы Пифагора можно решать не только математические задачи, но и широко использовать ее в практической деятельности человека. Теорема Пифагора нашла своё применение в строительстве и архитектуре, мобильной связи.

И даже я, ученица 9 класса, смогла найти ей практическое применение. Правда, вместо летней кухни мы решили построить новую баню. И думаю, что при ее строительстве нам очень понадобятся мои знания по математике.

Результатом моей работы является:

1. приобретение навыка работы с литературными источниками;

2. научилась работать с большим объёмом информации, отбирать нужную информацию;

3. это мой первый проект по математике, в результате которого я приобрела опыт обработки данных и написания исследовательского проекта.

Было интересно почувствовать себя исследователем, но главное меня заинтересовал процесс познания. Работа над проектом помогла мне реально применить полученные на уроках знания, навыки, опыт в практической деятельности, в соответствии с моими интересами.

Список использованной литературы

1. Асмус В. Ф. «Античная философия». М.: «Высшая школа» 1996г.

2Афанасьев В.В. «Формирование творческой активности студентов в процессе решения математических задач». Ярославль. 1996 г.

3. Атанасян М.С. «Геометрия» 7-9 класс. М.: Просвещение, 2011 г.

4. Большая математическая энциклопедия для школьников. 2011 г.

5. Волошинов А.В. «Пифагор» М.: 1993г.

6. Глейзер Г.И. История математике в школе VII-VIII классы, пособие для учителей. М.: Просвещение. 1992г.

7. «Математика». Издательский дом «Первое сентября» № 3. 1997 г.

8. Колосов А.А. «Книга для внеклассного чтения по математике в старших классах». М.: 2003 г.

9. Скопец З.А.Геометрические миниатюры, М.: Просвещение,2000г.

10. Шепан Еленьский «По следам Пифагора». Детгиз 1961г.

1. http://ru.wikipedia

2. www.exponenta.ru