Просмотр содержимого документа
«Проекция перемещения»

 x 0 , то S х 0 ( положительна). " width="640"
x 0 , то S х 0 ( положительна). " width="640"
S x
х
0
х 0
х
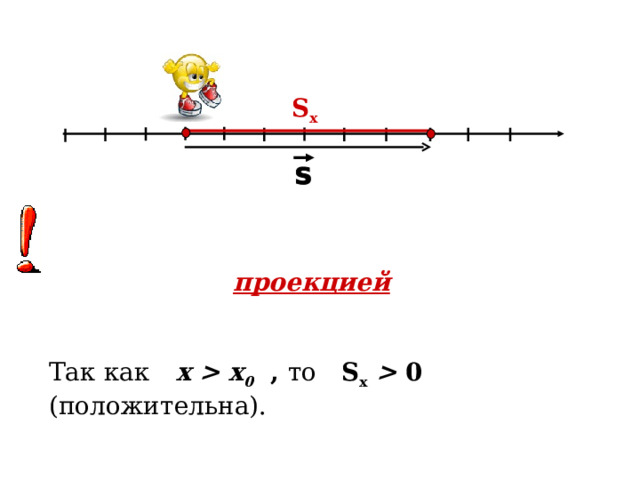
Величина, равная разности конечной и начальной координаты тела, называется проекцией перемещения.
S x = x – x 0 - проекция перемещения на ось ОХ
Так как x x 0 , то S х 0 ( положительна).
Sx
х
0
х 0
х
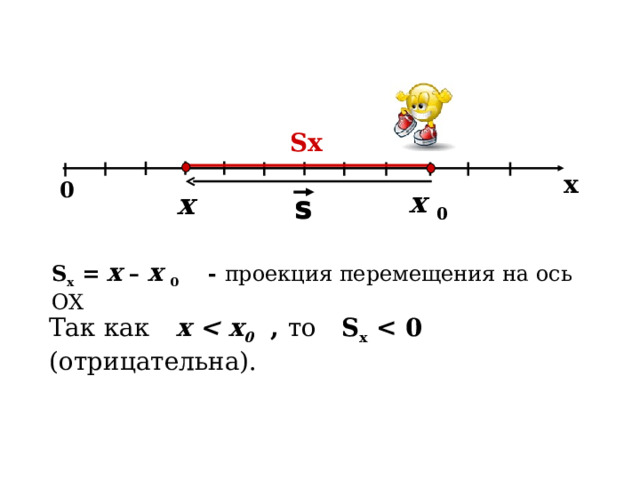
S x = x – x 0 - проекция перемещения на ось ОХ
Так как x 0 , то S х ( отрицательна).
х
0
x
x 0
=
x 0
x
=
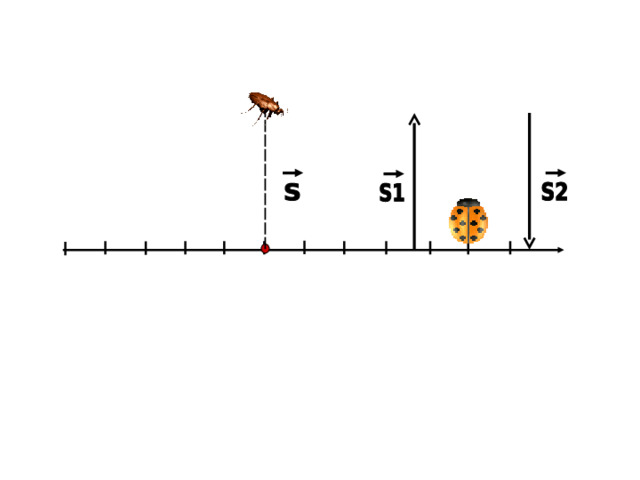
= x – x 0
Так как x = x 0 , то S х = 0 .
 0 Если вектор перемещения противоположно направлен оси координат, то его проекция отрицательна. S OX S x Если вектор перемещения перпендикулярен оси координат, то его проекция равна нулю. S OX S x = 0 " width="640"
0 Если вектор перемещения противоположно направлен оси координат, то его проекция отрицательна. S OX S x Если вектор перемещения перпендикулярен оси координат, то его проекция равна нулю. S OX S x = 0 " width="640"
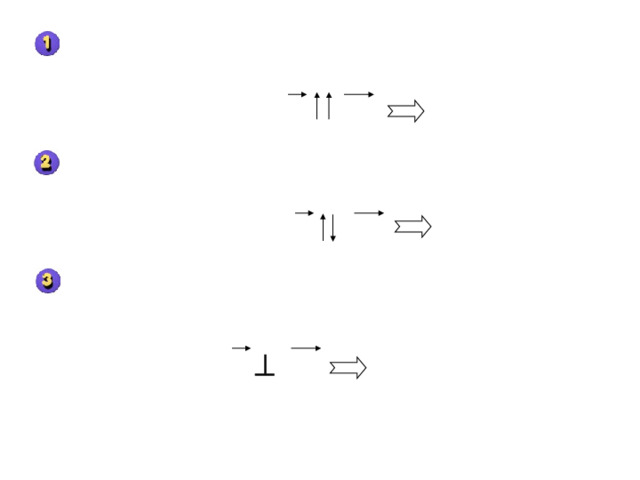
Если вектор перемещения сонаправлен с координатной осью, то его проекция положительна. S OX S x 0
Если вектор перемещения противоположно направлен оси координат, то его проекция отрицательна. S OX S x
Если вектор перемещения перпендикулярен оси координат, то его проекция равна нулю.
S OX S x = 0
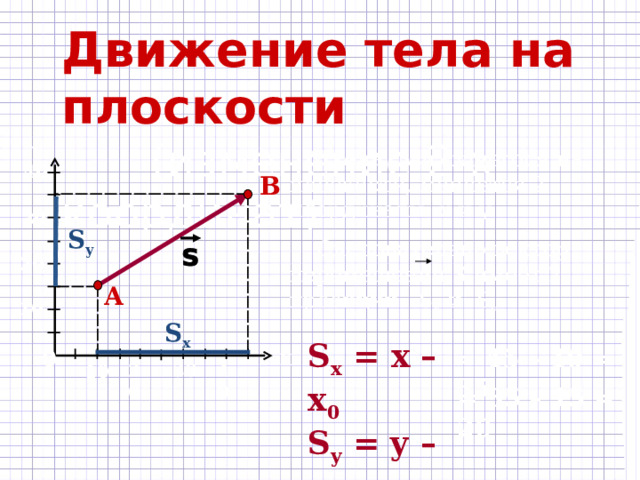
Движение тела на плоскости
(изменение 2-х координат).
Y
У тела, движущегося на плоскости, меняется 2 координаты: x и y .
Следовательно вектор перемещения S имеет 2 проекции: S x и S y .
40
В
30
S y
20
А
10
S x
S x = x – x 0
S y = y – y 0
= 45 – 10 = 35
0
Х
30
40
20
10
= 35 – 15 = 20
Y
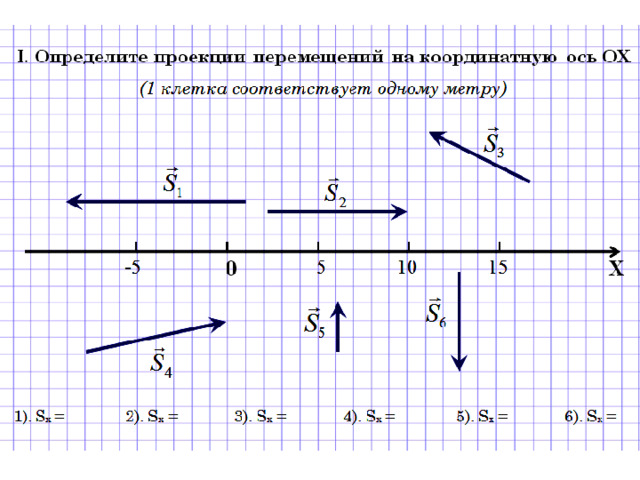
1) . S x =
S y =
2) . Sx =
Sy =
3). Sx =
Sy =
4). Sx =
Sy =
4
S 1
S 3
2
0
Х
2
- 2
6
- 6
4
- 4
- 2
S 2
- 4
S 4

S 6
S 5
S 7
S 8

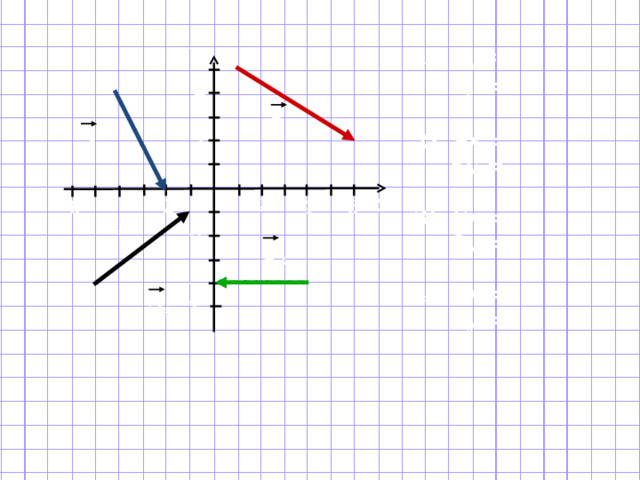
I вариант
II вариант
1) . S x = -2
S y = -4
3) . S x = 0
S y = 3
5 ). S x = 0
S y = - 5
7 ). S x = 3
S y = -2
2) . S x = 3
S y = 4
4) . S x = - 2
S y = 2
6 ). S x = -3
S y = 5
8). S x = 3
S y = 0

Определение перемещения тела по его проекциям
S x = x – x 0
S y = y – y 0
Y
= 5 – 1 = 4
8
В
= 6 – 3 = 3
6
S y
с 2 = а 2 + в 2
4
А
2
S x
0
Х
3
4
2
1
5
= 5
Зная начальное положение тела и проекции его перемещения за определенный интервал времени, можно найти конечные координаты.
Дано:
x 0
y 0
S х
S y
x - ?
y -?
S x = x – x 0
S y = y – y 0
x = S x + x 0
y = S y + y 0






 x 0 , то S х 0 ( положительна). " width="640"
x 0 , то S х 0 ( положительна). " width="640"


 0 Если вектор перемещения противоположно направлен оси координат, то его проекция отрицательна. S OX S x Если вектор перемещения перпендикулярен оси координат, то его проекция равна нулю. S OX S x = 0 " width="640"
0 Если вектор перемещения противоположно направлен оси координат, то его проекция отрицательна. S OX S x Если вектор перемещения перпендикулярен оси координат, то его проекция равна нулю. S OX S x = 0 " width="640"

















