Разработка урока по теме:
«Программирование алгоритмов с «ветвлением» и «циклом»
на языке Паскаль» (9 класс)
Тип урока: Комбинированный.
Цель урока: Обобщить и систематизировать знания учащихся по данной теме с помощью проблемно – поискового метода при решении задач по информатике.
Задачи урока:
Обучающие:
– выявить качество и уровень овладения знаниями и умениями по теме «Алгоритмизация и программирование», полученными на предыдущих уроках;
– продолжить формировать практические навыки по составлению блок-схем и программ;
– показать взаимосвязь математики и информатики. Научить использовать знания, полученные на уроке математики при решении задач по информатике;
Развивающие:
– развивать логическое мышление, умение обобщать, сопоставлять и применять полученные знания на практике;
– развивать навыки индивидуальной и групповой практической работы;
– развивать познавательную деятельность учащихся, прививать интерес к составлению программ, развивать умение анализировать происходящие изменения в решении задач;
Воспитательные:
– развивать познавательный интерес, творческую активность, интеллект;
– развивать интуицию, эрудицию, самостоятельность в суждениях, упорство в достижении цели;
– развивать культуру общения, воспитывать внимание, сообразительность, находчивость, тренировку памяти, умение работать в группе.
Оборудование и наглядные средства обучения: компьютеры с установленной ОС Windows 7, 10, проекционная техника, программа PascalABC, раздаточный материал.
ХОД УРОКА
Организационный этап
Приветствие. Проверка присутствующих.
Проверка домашнего задания
На дом были заданы 2 задачи:
| Задача 1. Составить программу вычисления степени числа a с натуральным показателем n. Program dz1; var a,n,i,p:integer; begin write (‘n=’); readln(n); write (‘a=’); readln(a); p:=1; for i:=1 to n do p:=p*a; write(‘p=’,p); end. | Задача 2. Найти значение выражения 1*1+2*2+…+n*n.
Program dz2; var n,s,i:integer; begin write (‘n=’); readln(n); s:=0; for i:=1 to n do s:=s+i*i; writeln(‘s=’,s); end. |
Актуализация знаний
– Какие структуры называют ветвлением? (Конструкция ветвления включает в себя проверку истинности или ложности условия.)
– Какие конструкции ветвления бывают? (Полная и неполная.)
– Какие структуры называют циклом? (Циклом называют повторение одних и тех же действий (шагов).)
– Назовите виды циклов. (Цикл с предусловием, цикл с постусловием и цикл со счетчиком.)
– Что будет выведено на экран после выполнения фрагмента программы?
begin
a:=1; b:=2;
if (a=1) and (b=2) then n:=a+b else n:=a-b;
writeln(n);
end. (Ответ: 3)
– Чему будет равняться k после выполнения программы?
var m,k:byte;
begin
m:=1; k:=0;
while (m
writeln(k)
end. (Ответ:5)
– Чему будет равняться х после выполнения фрагмента программы?
х:=0;
repeat x:=x+8 until x=21; (Ответ:24)
– Сколько раз выполнится цикл и что будет выдано на печать?
var i,k:integer;
…
k:=0;
for i:=10 downto 10 do k:=i; write (k); (Ответ:1 раз, 10)
Постановка целей урока
Сегодня на уроке мы порешаем задачи на языке программирования Паскаль.
Работа по теме урока. Практическая работа
Я предлагаю следующие задачи для решения в классе.
ЗАДАЧА № 1. Найти наибольшее число из трех заданных чисел. На доске записываю несколько троек чисел: 568, 742, 390.
Учащиеся называют максимальное число: 742.
Вопрос: “Каким образом вы определили, что данное число максимальное?”.
Учащиеся: Мы сравнили числа друг с другом.
Проблема: “А как компьютер сравнит три числа?”
Я обращаю внимание ребят, что машина может сравнивать только два числа.
Обозначим одно число буквой А, второе число буквой B, третье число – буквой С.
Учащиеся: Предлагают такой вариант решения проблемы: надо сравнивать первые два числа, а затем, большее из них с третьим числом.
Учитель: Нарисуйте в тетради блок – схему для сравнения трех чисел.
Учащиеся в тетради рисуют блок – схему, а затем сравнивают составленную ими схему с блок - схемой на проекционном экране. Одному из учащихся предлагаю сделать анализ блок – схемы. А теперь в соответствии с блок – схемой составьте программу.
Учащиеся самостоятельно составляют программу.
Учитель: Проверьте правильность работы программы на компьютере, введите заданные числа и посмотрите результат.
Проблема: А может ли измениться исходное значение переменной А в процессе работы программы?
Ответ: Да.
Учитель: А как? Ответ обоснуйте.
Решение:
1. Находим наибольшее из первых двух данных чисел A и B, а затем – максимальное из полученного числа и третьего данного числа С.
Program MAX1;
var A, B, C, max: real;
begin
writeln (‘Введите три числа A, B, C’);
readln (A, B, C);
if AB then max:=A else max:=B;
if C max then max:=C;
writeln(‘Максимальное значение =’,max);
end.
Учитель: Как вы думаете, можно ли решить задачу другими способами?
Учащиеся получают задание на уроке и продолжают поиск решения задачи.
Предполагаемые решения учащихся:
2 способ. При решении задачи можно проверить, является ли первое число A максимальным и если не является, то сравниваем второе и третье число B и C.
Program MAX2;
var A, B, C, max: real;
begin
writeln (‘Введите три числа A, B, C’);
readln (A, B, С);
if (AB) and (AC) then max:=A;
if BC then max:=B else max :=C;
writeln(‘Максимальное значение =’, max);
end.
3 способ. Можно решить задачу, сравнивая попарно все числа .
Program MAX3;
var A, B, C, max: real;
begin
writeln(‘Введите три числа A, B, C’);
readln(A, B, C);
if (AB) and (AC) then max:= A;
if (BA) and (BC) then max:=B;
if (CA) and (CB) then max:=C;
writeln(max:6:2);
end.
Чтобы убедиться в правильности выполнения программы, желательно рассмотреть ее выполнение с помощью таблицы значений. При проверке правильности выполнения программы необходимо рассматривать все возможные варианты АВС, АСВ, ВСА, СВА, ВАС, САВ.
Проблема: А можно написать программу, чтобы она выстраивала числа в порядке возрастания или убывания?
Ученики предлагают свои варианты решения данной проблемы.
Варианты решения задачи:
Программа выстраивает числа в порядке убывания.
Program MAX4;
var A, B, C, max: real;
begin
writeln(‘Введите три числа A, B, C’);
readln(A, B, C);
if (AB) and (AC) and (BC) then writeln (A, ‘ ‘,B,’ ‘,C);
if (BC) and (BA) and (AC) then writeln (B, ‘ ‘,A,’ ‘,C);
if (CA) and (CB) and (AB) then writeln (C, ‘ ‘,A,’ ‘,B);
if (AB) and (AC) and (CB) then writeln (A, ‘ ‘,C,’ ‘,B);
if (BC) and (BA) and (CA) then writeln (B, ‘ ‘,C,’ ‘,A);
if (CA) and (CB) and (BA) then writeln (C, ‘ ‘,B,’ ‘,A);
end.
Программа печатает максимальное число, минимальное число и среднее число.
Program MAX5;
var A, B, C, max, min, sr : real;
begin
writeln(‘Введите три числа A, B, C’);
readln(A, B, C);
if AB then max:=A else max:=B;
if C max then max:=C;
if A if C if (AB) and (A if (BA) and (B if (CA) and (C if (BC) then sr:=B;
if (AC) then sr:=A;
if (CB) then sr:=C;
writeln (‘max=’, max:6:2);
writeln (‘sr=’, sr:6:2);
writeln (‘min=’, min:6:2);
end.
ЗАДАЧА № 2. Даны три натуральных числа. Найти их наибольший общий делитель.
Вопрос: Какие существуют методы нахождения НОД?
Ответ: Существуют различные методы нахождения наибольшего общего делителя нескольких натуральных чисел:
1. разложения на простые сомножители,
2. алгоритм Евклида,
3. целочисленное деление.
Найти НОД чисел 48, 36, 24
Разложим на множители числа:
48 = 2 * 2 * 2 * 2 *3
36 = 2 * 2 * 3 * 3
24 = 2 * 2 * 2 * 3
Из множителей вычеркиваем те, которые не входят в разложение второго и третьего числа – это числа 2 * 2 * 3 =12
Учитель: Сделайте вывод для тройки чисел x, y, z.
Проблема: Какие же знания и умения необходимы для построения алгоритма нахождения НОД?
Для того чтобы построить алгоритм, необходимо уметь:
определять все простые множители в пределах заранее неизвестных чисел х и у, z;
хранить эти простые множители и обращаться к ним;
хранить все сомножители для чисел х и у, z;
выбирать из трех множеств одинаковые элементы.
Сделайте анализ.
Каждая часть задачи сложна для алгоритмизации. Построение массива простых чисел требует проверки, является ли число простым, т.е. не делится ли оно на все простые числа, меньше данного.
Второй метод решения – рекурсивный. Его общепринятое название алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) двух целых неотрицательных чисел.
НОД (х, у) вычисляется в соответствии со следующим правилом:
НОД (х, у)= 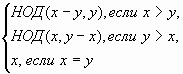
Мы разбирали решение задачи для нахождения НОД двух чисел.
Для решения данной задачи воспользуемся циклом с постусловием.
Третий метод решения – это целочисленное деление.
Пусть х и у – одновременно не равные нулю целые неотрицательные числа, и пусть х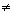 у. Если у = 0, то НОД (х, у) = х, а если у
у. Если у = 0, то НОД (х, у) = х, а если у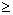 0, то для чисел х, у и r, где r остаток от деления х на у, выполняется равенство НОД (х, у) = НОД (у, r).
0, то для чисел х, у и r, где r остаток от деления х на у, выполняется равенство НОД (х, у) = НОД (у, r).
В соответствие со следующим правилом:
НОД(48, 18) = НОД(18, 12) = НОД(12, 6) = 6.
Первое число делим нацело на второе. Очевидно, что остаток целочисленного деления меньше второго числа. Если остаток равен нулю, то это значит, что первое число нацело делится на второе, и в этом случае второе число и будем считать НОД (в соответствие с определением). Если остаток не равен нулю, то заменим первое число на второе, а второе – на остаток, и будем повторять действия до тех пор, пока остаток не станет равным нулю.
Запишем алгоритм решения задачи:
1. Ввод натуральных чисел х, у.
2. Найдем r – остаток от деления х нацело на у.
3. Если r = 0, то найдем значение у, иначе х:=у; у:= r.
4. Найдем r – остаток от деления х нацело на у.
Вычислить значение х
Порядок действий имеет большое значение. Результат выполнения операций x:=x; y:=r отличен от результата выполнения операций
y: = r; x: =y.
Проблема: А правильно ли мы составили алгоритм?
Задание на дом: Докажите правильность алгоритма.
Решение задачи для нахождения НОД двух чисел.
Program NOD_1;
var x, y:integer;
begin
writeln(‘Введите два числа’);
readln (x, y);
repeat
if x y then x:= x mod y else y:= y mod x;
until (x = 0) or (y = 0);
{до тех пор, пока одно из чисел не станет равно нулю}
writeln (‘НОД=’, x + y);
{Вывод НОД. Одно из чисел обязательно равно нулю}
readln;
end.
Машина может находить НОД двух чисел.
Проблема: Как составить программу для нахождения НОД трех чисел?
Учащиеся: Сначала находим НОД двух чисел, а затем находим НОД третьего числа.
НОД (a, b, c) = НОД (НОД(a, b), c).
Я предлагаю ученикам самим решить задачу.
Один из способов решения задачи, предлагаемый учениками приведен ниже.
Программа на Паскале:
Program NOD_2;
var A, B,C, S:integer;
begin
readln(A, B, C);
repeat
if AB then A:=A mod B
else B:=B mod A;
until (A = 0) or ( B = 0);
writeln (‘НОД=’, A + B);
S:=A + B;
repeat
if S C then S:= S mod C else C:= C mod S;
until (S = 0) or ( C = 0);
writeln (‘НОД=’, S + C);
{Вывод НОД. Одно из чисел обязательно равно нулю}
readln;
end.
Предложенные методы и соответствующие им алгоритмы существенно не различаются, но для конкретных выбранных значений обнаруживается существенная разница в количестве операций при решении задачи. Оценить заранее, какой метод будет эффективнее для конкретных исходных данных, не возможно, так, как нельзя оценить, сколько раз будет выполняться тело цикла (количество повторов).
Для учеников проблема состоит еще и в том, чтобы выбрать метод, который будет более эффективен и прост в решении.
Подведение итогов урока
– Как программируется на языке Паскаль полное и неполное ветвление?
– Как программируется цикл с постусловием на языке Паскаль?
– Для каких целей лучше его использовать?
Выставление оценок за урок.
Домашнее задание:
Написать программу нахождения минимального числа из трех заданных чисел.
Найти НОД трех чисел любым удобным для вас способом.