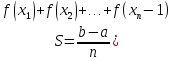Содержание:
Вступление
История открытия числа π
Интересные факты об истории числа
4. Способы вычисления числа π
4.1 Вычисление числа π с помощью нити
4.2 Вычисление числа π с помощью взвешивания
4.3 Вычисление числа π с помощью падающей иголки
4.4 Вычисление числа π методом Архимеда
5. Как запомнить число π
6. Вывод
7. Литература
Вступление.
С момента появления человека на Земле важность чисел для его жизни, а затем и соотношений между ними постоянно возрастала. Численное значение есть и остается определяющим фактором оценки результата в научно-исследовательской практике. В повседневной жизни великое множество чисел окружает современного человека на каждом шагу. Числа повсюду! Пронумерованы автомашины, дома и квартиры. Площадь жилья, объем потребляемой воды, газа, электроэнергии — все это числа. Как, впрочем, и код персональных денежных карточек и их денежное содержимое. Наконец, возраст человека, его вес и размеры — тоже числа. Числа, числа, числа… обладающие разными свойствами, входящие в числовые множества, относящиеся к различным системам мер и весов. Среди всего разнообразия чисел особо выделяются знаменитые, и даже таинственные. Число π, о котором пойдет речь в моей работе, с незапамятных времен привлекало внимание людей своими свойствами. С числом π связано много интересного и необъяснимого, это – знаменитая математическая константа, появляющаяся в самых неожиданных местах. Люди изучают его уже более 4000 лет. Меня заинтересовало это число во время изучения темы «Длина окружности». В нашей действительности оно используется практически везде - от расчётов прогноза погоды до больших данных по мировой статистике Также это число встречается при решении прикладных задач. С помощью открытия интересных фактов о числе π, можно лучше запомнить его. Я считаю, что моя работа поможет мне открыть много нового и интересного о числе π.
Цель моей работы - исследовать природу числа π, узнать новые, интересные факты про число π, узнать способы запоминания и получения этого числа.
Задачи:
изучить литературу по данной теме;
2. История открытия числа π.
Проверенный факт: стоит только услышать о числе π, как сразу же где-то внутри возникает ощущение непостижимости. Казалось бы: разделите длину окружности на диаметр этой самой окружности, и в результате у вас — неизменное число π. Всё! Откуда загадочность, таинственность, непостижимость? Учтем, что постоянство отношения длины любой окружности к ее диаметру было замечено уже давно. Первые подтверждения тому есть на клинописных глиняных табличках, которые относятся к шумеро-вавилонской цивилизации III тысячелетия до нашей эры. Правда, древний след числа π был тогда еще весьма приблизительный: 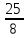 . А для практических нужд нередко брали целое значение числа π, равное 3. Но хозяйственная практика человечества стремительно развивалась, вместе с ней совершенствовалась и теория: математические исследования и вычисления. Вавилоняне уже использовали несколько систем счисления, применяли различные системы мер и весов, знали основные метрические соотношения в треугольнике. А бурное развитие строительства и аграрного хозяйства заставило их изобрести достаточно практичные способы вычисления площадей и объемов самых невообразимых фигур и форм. К этому времени уже были составлены обширные таблицы квадратов и кубов чисел, значений квадратных и кубических корней. Таким образом, в наследство египетской цивилизации достался впечатляющий математи ческий потенциал. И египтяне его талантливо приумножили! Это подтверждают многочисленные древнеегипетские папирусы. Отсюда и ста- ло известно, что при дворе фараона Аменемхета III (2000 лет до нашей эры) в качестве писца состоял египтянин Ахмес, который, судя по всему, неплохо разбирался в математике. Ахмес тщательно собрал и записал почти все сведения из области математики, которые были на то время известны египтянам. Составленный им папирус шириной 30 см получился весьма внушительной длины — 5 м 25 см. Документ, составленный около 1550 года до нашей эры, настолько примечателен, что даже имеет имя собственное — папирус Ринда. Дело в том, что в 1858 году, когда был обнаружен этот папирус, Генри Ринд, один из меценатов того времени, приобрел его во владение. Теперь одна часть данного документа хранится в Нью-Йорке, а другая — в Лондоне.
. А для практических нужд нередко брали целое значение числа π, равное 3. Но хозяйственная практика человечества стремительно развивалась, вместе с ней совершенствовалась и теория: математические исследования и вычисления. Вавилоняне уже использовали несколько систем счисления, применяли различные системы мер и весов, знали основные метрические соотношения в треугольнике. А бурное развитие строительства и аграрного хозяйства заставило их изобрести достаточно практичные способы вычисления площадей и объемов самых невообразимых фигур и форм. К этому времени уже были составлены обширные таблицы квадратов и кубов чисел, значений квадратных и кубических корней. Таким образом, в наследство египетской цивилизации достался впечатляющий математи ческий потенциал. И египтяне его талантливо приумножили! Это подтверждают многочисленные древнеегипетские папирусы. Отсюда и ста- ло известно, что при дворе фараона Аменемхета III (2000 лет до нашей эры) в качестве писца состоял египтянин Ахмес, который, судя по всему, неплохо разбирался в математике. Ахмес тщательно собрал и записал почти все сведения из области математики, которые были на то время известны египтянам. Составленный им папирус шириной 30 см получился весьма внушительной длины — 5 м 25 см. Документ, составленный около 1550 года до нашей эры, настолько примечателен, что даже имеет имя собственное — папирус Ринда. Дело в том, что в 1858 году, когда был обнаружен этот папирус, Генри Ринд, один из меценатов того времени, приобрел его во владение. Теперь одна часть данного документа хранится в Нью-Йорке, а другая — в Лондоне.
Впервые обозначением этого числа греческой буквой {\displaystyle \pi }![]() воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году.
воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году.
Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.
История числа {\displaystyle \pi }π шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на 3 периода: древний период, классическая эра, и эра цифровых компьютеров.
{\displaystyle \pi }Архимед, возможно, первым предложил математический способ вычисления {\displaystyle \pi }. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку {\displaystyle 3+{\frac {10}{71}} и предположил, что {\displaystyle \pi }π примерно равняется 22/7 ≈ 3,142857142857143.
Чжан Хэн во II веке уточнил значение числа π {\displaystyle \pi }, предложив два его эквивалента: 1) 92/29 ≈ 3,1724…; 2) {\displaystyle {\sqrt {10}}}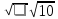 ≈ 3,1622.
≈ 3,1622.
Около 265 года н. э. математик Лю Хуэй из царства Вэй предоставил простой и точный итеративный алгоритм для вычисления {\displaystyle \pi }π с любой степенью точности. Он самостоятельно провёл вычисление для 3072-угольника и получил приближённое значение для {\displaystyle \pi }π по следующему принципу:
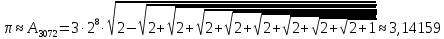
![]() Позднее Лю Хуэй придумал быстрый метод вычисления {\displaystyle \pi }
Позднее Лю Хуэй придумал быстрый метод вычисления {\displaystyle \pi }![]() и получил приближённое значение 3,1416 только лишь с 96-угольником, используя преимущества того факта, что разница в площади следующих друг за другом многоугольников формирует геометрическую прогрессию со знаменателем 4.
и получил приближённое значение 3,1416 только лишь с 96-угольником, используя преимущества того факта, что разница в площади следующих друг за другом многоугольников формирует геометрическую прогрессию со знаменателем 4.
В 480-х годах китайский математик Цзу Чунчжи продемонстрировал, что {\displaystyle \pi }π ≈ 355/113, и показал, что 3,1415926 {\displaystyle \pi }π {\displaystyle \pi }π в течение последующих 900 лет.
До II тысячелетия было известно не более 10 цифр {\displaystyle \pi }π. Дальнейшие крупные достижения в изучении {\displaystyle \pi }π связаны с развитием математического анализа, в особенности с открытием рядов, позволяющих вычислить {\displaystyle \pi }π с любой точностью, суммируя подходящее количество членов ряда.
Эпоха цифровой техники в XX веке привела к увеличению скорости появления вычислительных рекордов. Джон фон Нейман и другие использовали в 1949 году ЭНИАК для вычисления 2037 цифр {\displaystyle \pi }π, которое заняло 70 часов. Ещё одна тысяча цифр была получена в последующие десятилетия, а отметка в миллион была пройдена в 1973 году (десяти знаков числа {\displaystyle \pi } {\displaystyle (\pi =3{,}141592653\ldots )}π вполне достаточно для всех практических целей).
Так за полвека вырастала запись точного значения числа «Π» с помощью компьютера:
1949 год — 2037 десятичных знаков
1958 год — 10000 десятичных знаков
1961 год — 100000 десятичных знаков
1973 год — 10000000 десятичных знаков
1986 год — 29360000 десятичных знаков
1987 год — 134217000 десятичных знаков
1989 год — 1011196691 десятичный знак
1991 год — 2260000000 десятичных знаков
1994 год — 4044000000 десятичных знаков
1995 год — 4294967286 десятичных знаков
1997 год — 51539600000 десятичных знаков
1999 год — 206 158 430 000 десятичных знаков.
В 2009 году французский программист Фабрис Беллар поставил рекорд вычисления числа π с точностью до 2,7 трлн знаков после запятой. Что самое удивительное, он сделал это на своём персональном компьютере под управлением Fedora 10.
Достижение Беллара показало, что не обязательно иметь суперкомпьютер для таких вычислений, и его коллеги решили сделать компьютер помощнее и перекрыть достижение француза.
2 августа 2010 года американский студент Александр Йи и японский исследователь Сигэру Кондо рассчитали последовательность с точностью в 5 триллионов цифр после запятой.
3. Интересные факты о числе π
Итак, число π - число, обозначающее соотношение длины окружности к длине её диаметра. Но вот дальше уже начинаются загадки...
Вычислить до конца эту величину невозможно, она равна 3,1415926535, далее после запятой – до бесконечности. Учёные считают, что последовательность цифр не повторяется, причём эта последовательность абсолютно случайна.
Загадка числа π на этом не заканчивается. Астрономы уверены, что тридцать девять знаков после запятой в данном числе достаточно для того, чтобы вычислить длину окружности, которая опоясывает известные космические объекты во Вселенной, с погрешностью в радиус атома водорода.
Число π иррационально, т.е. его нельзя выразить дробью. Эта величина трансцедентна – т.е. её нельзя получить, произведя какие-либо действия над целыми числами….
Число π тесно связано с понятием золотого сечения. Археологи выяснили, что высота Великой Пирамиды в Гизе относится к длине её основания, именно также как радиус окружности к её длине.
Число π имеет свой день рождения. Праздник был учрежден в 1987 году физиком из Сан-Франциско Ларри Шоу, который подметил, что в американской системе заπси дат (месяц / число) дата 14 марта - 3/14 - и время 1:59 совпадает с первыми разрядами числа π = 3,14159.С тех пор каждый год люди не равнодушные к математике отмечают день числа π.
Главная церемония проходит в музее. Кульминация приходится на 1час 59 минут 26 секунд после полудня. Участники праздника маршируют вдоль
стен Круглого зала. В центре зала размещают латунную тарелку, на которой выгравировано число π с первыми 100 знаками после запятой.
В этот день принято читать хвалебные речи в честь числа Π, его роли в жизни человечества, пекут и едят Π-рог с изображением греческой буквы Π или с первыми цифрами самого числа, пьют наπтки и играют в игры, начинающиеся на π, решают математические головоломки и загадки, водят хороводы вокруг предметов, связанных с этим числом. Итальянцы, наверное, в этот день готовят Πццу, англичане – жареную Πикшу, немцы ставят на стол свиной шΠИк, французы непременно готовят что-нибудь ΠИкантное. Нельзя не отметить такой факт, что об исследуемом мною числе π был снят фильм . Герой фильма (1999г) Даррена Ароновски молодой человек по имени Макс пытается найти на своём огромном компьютере, который занимает всю его комнату, значение числа π. А вернее, хочет найти систему в заπси числа, но пока в его голове только хаос.{\displaystyle {\pi }={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+\cdots }
4. Способы вычисления числа π
4.1 Вычисление числа π с помощью нити и линейки
Рассмотрим простейший способ нахождения числа π с помощью нити и линейки. Построим на квадратном листе картона круг произвольного радиуса и вырежем его. Измерим длину окружности, ограничивающую этот круг. Воспользуемся нитью и линейкой. Обмотаем нитью круг и отрежем часть нити, ограничивающую круг. Теперь измерим длину нити и длину диаметра круга. В нашем случае нить имела длину 44 см, а диаметр имел длину 14. Найдем отношение длины окружности к диаметру и получим число 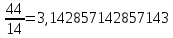 .
.
Вычисление числа π с помощью взвешивания.
Проведем эксперимент.
На листе картона начертим квадрат. Впишем в него круг. Вырежем квадрат. Определим массу картонного квадрата с помощью школьных весов. Итак, наш квадрат имеет массу 12 г 899мг. Вырежем из квадрата круг. Взвесим и его. Масса круга равна 10 г 120 мг. Зная массы квадрата (mкв) и вписанного в него круга (mкр), воспользуемся формулами
m = ρV, V =Sh, где ρ, h- соответственно плотность и толщина картона, S- площадь фигуры. Рассмотрим равенства:
mкв = ρSкв h = ρ4R2h ,
mкр = ρ Sкрh = ρπR2h.
Отсюда
mкр/ mкв = π/4, т.е.
π= 4 mкр/ mкв.
Итак, получили достаточно простую формулу, в которую подставим свои данные:
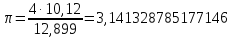
В первом и втором эксперименте я работала с одной и той же окружностью. Во втором эксперименте я получила более точное значение числа π
4.2 Вычисление числа π с помощью падающей иголки.
Число π приближенно найти можно с помощью иголки и теории вероятностей. Эта задача известна по имени французского естествоиспытателя Ж. Л. Л. Бюффона (1707-1788). Для осуществления опыта Бюффона требуется: плоская горизонтальная поверхность с нанесенными на ней параллельными равноотстоящими прямыми и игла. Расстояние между прямыми H и длина иглы L должны удовлетворять соотношениию L
p=2L/πH
А поскольку частота пересечений m/n примерно равна этой вероятности, для приближенного вычисления получим формулу для вычисления числа π
π=2Ln/Hm
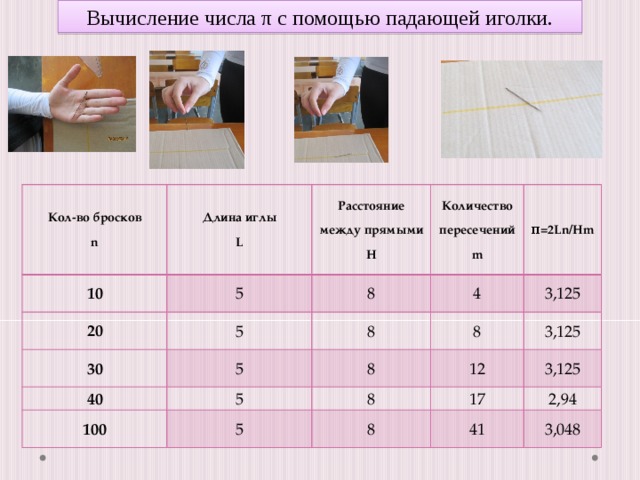
Я проделала опыт с иголкой 10,20,30,40 и 100 раз. Для эксперимента я взяла иглу длиной 5 см и расчертила лист бумаги параллельными линиями, расстояние между которыми 8 см.
Заполнила таблицу
| Кол-во бросков n | Длина иглы L | Расстояние между прямыми H | Количество пересечений m |
π=2Ln/Hm
|
| 10 | 5 | 8 | 4 | 3,125 |
| 20 | 5 | 8 | 8 | 3,125 |
| 30 | 5 | 8 | 12 | 3,125 |
| 40 | 5 | 8 | 17 | 2,94 |
| 100 | 5 | 8 | 41 | 3,048 |
В 19 веке, когда теория вероятностей рассматривалась как полуэкспериментальная наука, такие опыты имели большое значение и весьма тщательно ставились многими учеными. Вот известные результаты: Вольф - 1850 год 5000 бросаний опытное значение: 3,1596; Смит - 1855 год 3204 бросаний опытное значение: 3,1553; Фокс - 1894 год 1120 бросаний опытное значение: 3,1419; Лаццирини - 1901 год 3408 бросаний опытное значение: 3,1415929.
Вычисление числа π методом Архимеда
Суммирование площадей прямоугольников вписанных в полукруг.
Пусть А (а;0), В (b;0). Опишем на АВ полуокружность как на диаметре. Разделим отрезок АВ на п равных частей точками , 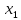 ,
,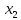
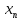 …, и восставим из них перпендикуляры до пересечения с полуокружностью. Длина каждого такого перпендикуляра — это значение функции f(x)=
…, и восставим из них перпендикуляры до пересечения с полуокружностью. Длина каждого такого перпендикуляра — это значение функции f(x)=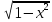 . Площадь S полукруга можно вычислить по формуле:
. Площадь S полукруга можно вычислить по формуле:
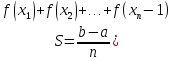
Тогда π ≈2S.
Значения π будут тем точнее, чем больше точек деления будет на отрезке АВ.
5. Как запомнить число π
У наших предков не было компьютеров, калькуляторов и справочников, но со времен Петра I они занимались геометрическими расчетами в астрономии, в машиностроении, в корабельном деле. Впоследствии сюда добавилась электротехника - там есть понятие "круговой частоты переменного тока". Для запоминания числа " π " было придумано двустишие (к сожалению, мы не знаем автора и места первой публикации его; но еще в конце 40-х годов двадцатого века московские школьники занимались по учебнику геометрии Киселева, где оно приводилось).
Чтобы нам не ошибиться ,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Надо только постараться
И запомнить все как есть:
Три, четырнадцать ,пятнадцать,
Девяносто два и шесть.
Три, четырнадцать, пятнадцать
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
Расположить цифры с соблюдение как бы стихотворного размера:
Три, четырнадцать, пятнадцать, девять два, шесть пять, три пять
Восемь девять, семь и девять, три два, три восемь, сорок шесть
Два шесть четыре, три три восемь, три два семь девять, пять ноль два
Восемь восемь и четыре, девятнадцать, семь, один. (3,1415926535897932384626433832795028841971)
6. Вывод
Изучив литературу по выбранной теме, познакомившись с историей природы числа π, я узнала много нового и интересного. Я поняла, что не все тайны числа π разгаданы.
В ходе проведения практического исследования я пришла к тому, что полученное на практике отношение длины окружности к её диаметру приближается к 3,14, но есть более точные способы получения значения исследуемого числа. И выполнила практическую работу по вычислению числа π различными методами. Самым точным оказался метод взвешивания, а самым простым метод с помощью нити. Достаточно неточными получились результаты опыта с бросанием иглы. Я думаю, что при увеличении числа бросаний, результат будет более точным.
Точное значение числа π в современном мире представляет собой не только собственную научную ценность, но и используется для очень точных вычислений (например, орбиты спутника, строительства гигантских мостов, а также оценки быстродействия и мощности современных компьютеров.
Я продолжу изучать применение числа π на уроках математики и физики
Литература:
Жуков А.В. Вездесущее число Π.- М.:URSS,2012, 240 с.
Звонкин А. Что такое p // Квант, 1978 №11.
Кымпан Ф. История числа p. - М.: Наука, Гл. ред. физ.-мат. лит., 1987, 138 с.
Райк А.Е. Очерки по истории математики в древности. - Саранск, 1987, 95 с.
Энциклопедия для детей / Математика. Издательство: «Аванта+» 1998 год.
История математики в школе ІХ – Х классы. Москва «Просвещение» 1983 год.
Википедия. Свободная энциклопедия. http://ru.wikipedia.org/
Научно-популярный ресурс для любознательных и интересующихся космосом. http://www.pro-kosmos.info/
Территория аномалий. http://strangefacts.ru/
Сайт журнала «Квант» - http://kvant.mirror0.mccme.ru/
Вайман А. А. Шумеро-вавилонская математика III–I тысячелетия до нашей эры. М.: ИВЛ, 1961.
Володарский А. И. Очерки истории средневековой индийской математики. М.: Наука, 1977.
Коваль С. От развлечения к знаниям. Математическая смесь / Пер. с польского. Wydawnictwa naukiwo-techiczne. Warszawa, 1975. 4. Таранов П. С. Анатомия мудрости:120 философов. Симферополь: Таврия, 1997. 5. Жуков А. В. О числе . М.: МЦНМО, 2002.
https://shkolazhizni.ru/culture/articles/14621/
9





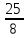 . А для практических нужд нередко брали целое значение числа π, равное 3. Но хозяйственная практика человечества стремительно развивалась, вместе с ней совершенствовалась и теория: математические исследования и вычисления. Вавилоняне уже использовали несколько систем счисления, применяли различные системы мер и весов, знали основные метрические соотношения в треугольнике. А бурное развитие строительства и аграрного хозяйства заставило их изобрести достаточно практичные способы вычисления площадей и объемов самых невообразимых фигур и форм. К этому времени уже были составлены обширные таблицы квадратов и кубов чисел, значений квадратных и кубических корней. Таким образом, в наследство египетской цивилизации достался впечатляющий математи ческий потенциал. И египтяне его талантливо приумножили! Это подтверждают многочисленные древнеегипетские папирусы. Отсюда и ста- ло известно, что при дворе фараона Аменемхета III (2000 лет до нашей эры) в качестве писца состоял египтянин Ахмес, который, судя по всему, неплохо разбирался в математике. Ахмес тщательно собрал и записал почти все сведения из области математики, которые были на то время известны египтянам. Составленный им папирус шириной 30 см получился весьма внушительной длины — 5 м 25 см. Документ, составленный около 1550 года до нашей эры, настолько примечателен, что даже имеет имя собственное — папирус Ринда. Дело в том, что в 1858 году, когда был обнаружен этот папирус, Генри Ринд, один из меценатов того времени, приобрел его во владение. Теперь одна часть данного документа хранится в Нью-Йорке, а другая — в Лондоне.
. А для практических нужд нередко брали целое значение числа π, равное 3. Но хозяйственная практика человечества стремительно развивалась, вместе с ней совершенствовалась и теория: математические исследования и вычисления. Вавилоняне уже использовали несколько систем счисления, применяли различные системы мер и весов, знали основные метрические соотношения в треугольнике. А бурное развитие строительства и аграрного хозяйства заставило их изобрести достаточно практичные способы вычисления площадей и объемов самых невообразимых фигур и форм. К этому времени уже были составлены обширные таблицы квадратов и кубов чисел, значений квадратных и кубических корней. Таким образом, в наследство египетской цивилизации достался впечатляющий математи ческий потенциал. И египтяне его талантливо приумножили! Это подтверждают многочисленные древнеегипетские папирусы. Отсюда и ста- ло известно, что при дворе фараона Аменемхета III (2000 лет до нашей эры) в качестве писца состоял египтянин Ахмес, который, судя по всему, неплохо разбирался в математике. Ахмес тщательно собрал и записал почти все сведения из области математики, которые были на то время известны египтянам. Составленный им папирус шириной 30 см получился весьма внушительной длины — 5 м 25 см. Документ, составленный около 1550 года до нашей эры, настолько примечателен, что даже имеет имя собственное — папирус Ринда. Дело в том, что в 1858 году, когда был обнаружен этот папирус, Генри Ринд, один из меценатов того времени, приобрел его во владение. Теперь одна часть данного документа хранится в Нью-Йорке, а другая — в Лондоне. 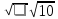
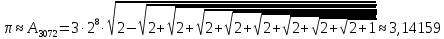
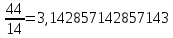 .
. 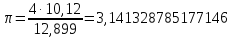
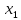 ,
,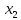
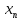 …, и восставим из них перпендикуляры до пересечения с полуокружностью. Длина каждого такого перпендикуляра — это значение функции f(x)=
…, и восставим из них перпендикуляры до пересечения с полуокружностью. Длина каждого такого перпендикуляра — это значение функции f(x)=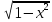 . Площадь S полукруга можно вычислить по формуле:
. Площадь S полукруга можно вычислить по формуле: