Производная функция. Механический и геометрический смысл

Производная функции

Механический и геометрический смысл

Дифференциальное исчисление

Дифференциальное исчисление дает аппарат для исследования функций, поведение которых в достаточно малой окрестности каждой точки близко к поведению линейной функции. Центральные понятия дифференциального исчисления: производная и дифференциал .

Оформление Дифференциального исчисл ения в самостоятельную математическую дисциплину связано с именами И.Ньютона и Г.Лейбница . Они сформулировали основные положения Дифференциального исчисления и четко указали на взаимно обратный характер операций дифференцирования и интегрирования.

Основное понятие дифференциального исчисления

• Производная функции в точке является основным понятием дифференциального исчисления

• Она характеризует скорость изменения функции в указанной точке
• Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости различного рода процессов
• Русский термин "производная функции" впервые употребил русский математик В.И. Висковатов (1780 - 1812)

Историческая справка

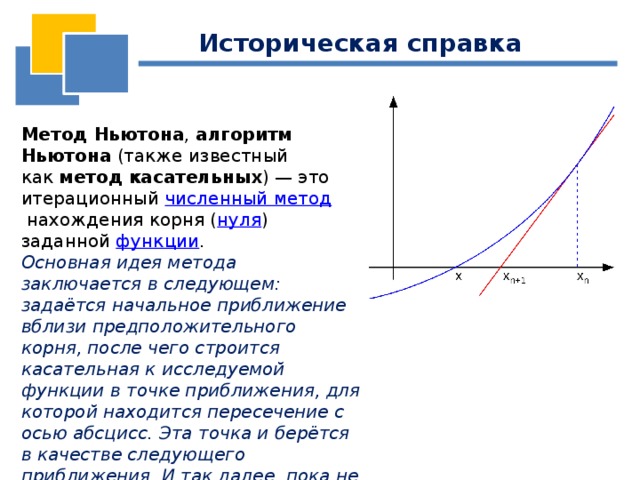
Метод Ньютона ,  алгоритм Ньютона  (также известный как  метод касательных ) — это итерационный  численный метод  нахождения корня ( нуля ) заданной  функции .

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Определение производной

Производной функции  называется  предел   отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

(x)=

Вычисление производной по определению

Дана функция f(x)=-3x Вычислить ее производную

1

(f(x)) =

Механический, геометрический,

экономический смысл производной

(t o )=V(t o )

Производная пути по времени равна мгновенной скорости в точке t o

(x o )=k=tg(α)

Производная есть угловой коэффициент (tg угла наклона) касательной, проведенной к кривой  f(x) в точке x o  

(t o )=V(t o )

Производная объема произведенной продукции по времени  есть производительность труда в момент  t o

Таблица производных

=0

=1 =

= =

=

=

=

Правила дифференцирования

=c

=

=

=

=(g)

Основные теоремы дифференциального исчисления

Теорема (Ролля)

Теорема (Лагранжа)

Пусть функция f(x) непрерывна на [a,b] и дифференцируема на (a,b) ,

Пусть функция f(x) непрерывна на [a,b] и дифференцируема на (a,b). Тогда внутри отрезка существует по крайней мере одна точка c, такая, что

f(a) = f(b). Тогда внутри отрезка существует по крайней мере одна точка c, такая, что f(c) =0

f'(c) = (f(b)-f(a))/(b-a).

Число

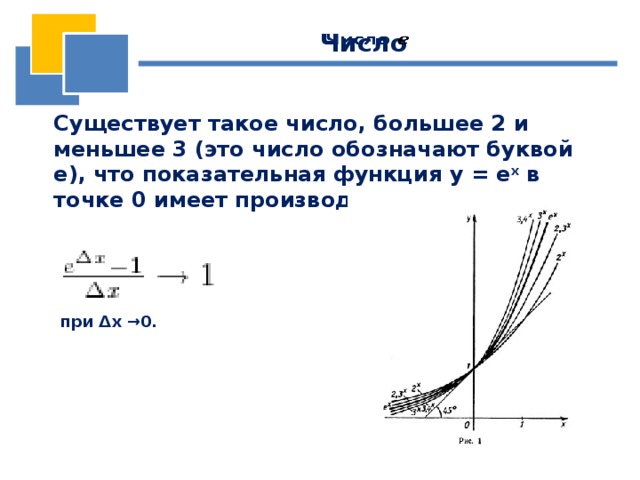
Существует такое число, большее 2 и меньшее 3 (это число обозначают буквой е), что показательная функция у = е x  в точке 0 имеет производную, равную 1, т. е.

при Δx →0.

Значение числа

  Доказано, что число е иррационально и поэтому записывается в виде бесконечной десятичной непериодической дроби. С помощью электронных вычислительных машин найдено более двух тысяч десятичных знаков числа е. Первые знаки таковы:

е = 2,718281828459045... . Функцию y=е x  часто называют экспонентой .

Использование числа

Причина «вездесущности» числа  e  заключается в том, что формулы математического анализа, содержащие экспоненциальные функции или логарифмы, записываются проще, если логарифмы брать по основанию  e , а не 10 или какому-либо другому основанию. Например, производная от (log 10  x)  = (1/ x )log 10  e , тогда как (log e  x)  =1/ x

(2 x  ) =2 x log e  2 , тогда как ( e х ) = e x

1

1

1

1

Использование числа

Предположим, что в некотором банке годовая процентная ставка равняется 100%. Такие ставки по банковским вкладам действительно были в России в первой половине 90-х годов минувшего столетия. Далее предположим, что если вклад пролежал на счете a дней, то банк начисляет за этот срок проценты по вкладу в размере *100%

Выясним можно ли при указанных условиях вклада получить больше 100% годовых?

Если мы поместим одну денежную единицу (скажем, 1 тысячу рублей ) на полгода, то, сняв вклад в размере 1,5 (полутора) единиц через полгода и положив сразу же их в тот же банк, в конце года мы получим уже

(1 + 0.5)(1 + 0.5) = 2.25 единиц , то есть получим 125% годовых .

Нетрудно понять, что если мы в течение года будем n раз переоформлять вклад через равные периоды времени, то положив одну единицу в начале года, в конце года мы получим единиц, т. е. получим *100% годовых. Очевидно, что при любом натуральном n , мы таким образом получим больше 100% годовых .

Задачи ЕГЭ

Задача1 .Прямая

является касательной к графику функции

.

Найдите абсциссу точки касания.

Задача 2 .

Материальная точка движется прямолинейно по закону 

+7+4t+11, где  x — расстояние от точки отсчета в метрах,  t— время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени  t=4 с.

Задачи ЕГЭ

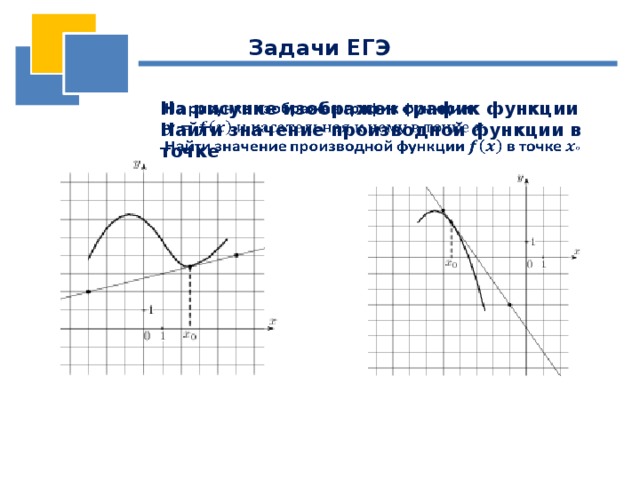
На рисунке изображен график функции

Найти значение производной функции в точке