Производная и её геометрический смысл. Правила дифференцирования.

Н

я

А

Е

А

Производная

Учитель математики МБОУ «Нижнедевицкая гимназия»

Быканова Л.И.

Содержание

• Понятие производной.
• Алгоритм нахождения производной.
• Примеры.
• Таблица производных.
• Физический смысл производной.
• Правила нахождения производных.
• Непрерывность функции.
• Геометрический смысл производной.

Понятие производной

Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке х этого интервала называют предел отношения приращения функции в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

∆ f

f ′(x) = lim

∆ x

∆ x →0

Нахождение производной называют дифференцированием

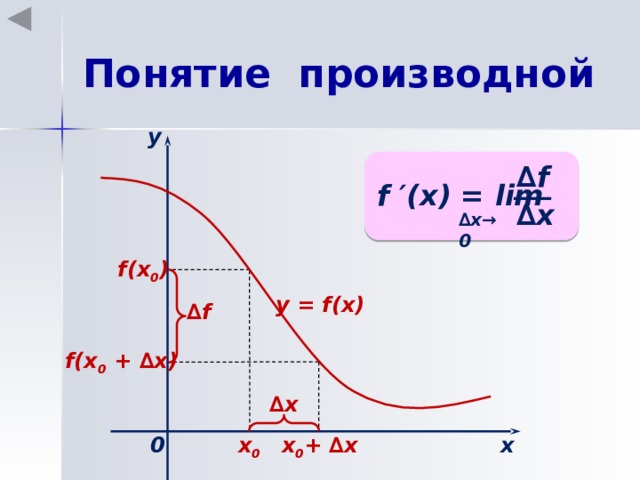
Понятие производной

у

∆ f

f ′(x) = lim

∆ x

∆ x →0

f(x 0 )

у = f(x)

∆ f

f(x 0 + ∆ х)

∆ х

х 0

х

0

х 0 + ∆ х

Алгоритм нахождения производной

• Зафиксировать значение х 0 , найти f(x 0 ) .

• Дать аргументу х 0 приращение ∆ х , перейти в новую точку х 0 + ∆ х , найти f(x 0 + ∆ х) .
• Найти приращение функции: ∆ f = f(x 0 + ∆ х) – f(x 0 ) .
• Составить отношение .
• Вычислить lim .
• Этот предел и есть f ′ (x 0 ) .

∆ f

∆ х

∆ f

∆ х

∆ x→0

Примеры

1. Найти производную функции y = kx + b в точке х o

Примеры

2. Найти производную функции y = C (C – const) в точке х o

Примеры

3. Найти производную функции y = x 2 в точке х o

Примеры

4. Найти производную функции y = √x в точке х o

Примеры

4. Найти производную функции y = √x в точке х o

Примеры

5. Найти производную функции y = 1/x в точке х o

Примеры

5. Найти производную функции y = 1/x в точке х o

Таблица производных

f (x)

C

f ′(x)

0

f (x)

kx + b

√ x

k

f ′(x)

x 2

1/(2 √ x)

e x

2x

x n

1/x

nx n–1

a x

e x

a x lna

– 1/x 2

tg x

sin x

1/cos 2 x

ctg x

cos x

cos x

– 1/sin 2 x

ln x

– sin x

1/x

log a x

1/(x lna)

Физический ( механический ) смысл производной

Если при прямолинейном движении путь s , пройденный точкой, есть функция от времени t , т.е. s = s(t) , то скорость точки есть производная от пути по времени, т.е. v(t) = s′(t) .

Производная выражает мгновенную скорость в момент времени t .

Правила нахождения производной

1. Если функции u(x) и v(x) имеют в точке х производные, то их сумма u(x) + v(x) также имеет в этой точке производную, причем

(u + v)′ = u′ + v′

2. Если функция u(x) имеет в точке х производную и С – данное число, то функция С ∙ u(x) также имеет в этой точке производную, причем

(Сu)′ = С∙u′

Правила нахождения производной

3. Если функции u(x) и v(x) имеют в точке х производные, то их произведение u(x) ∙ v(x) также имеет в этой точке производную, причем

(u ∙ v)′ = u′∙v + u∙v′

4. Если функция v(x) имеет в точке х производную и v(x) ≠ 0 , то функция также имеет в этой точке производную, причем

1

v(x)

v′

( )

′

1

= –

v

v 2

17

Правила нахождения производной

5. Если функции u(x) и v(x) имеют в точке х производные и v(x) ≠ 0 , то функция также имеет в этой точке производную, причем

u(x)

v(x)

( )

u

u′v – uv′

′

=

v

v 2

18

Производная сложной функции

( f ( g(x) ) ) ′ = f′ ( g(x) ) ∙g′(x)

Примеры:

1. ( (5x – 3) 3 ) ′ = 3(5x – 3) 2 ∙(5x – 3) ′ =

= 3(5x – 3) 2 ∙ 5 = 15(5x – 3) 2

2. ( sin(4x + 8) ) ′ = cos(4x + 8)∙(4x + 8) ′ =

= cos(4x + 8)∙4 = 4 cos(4x + 8)

Если функция имеет производную (дифференцируема) в точке х , то она непрерывна в этой точке.