Пояснительная записка
к экзаменационному материалу по математике для учащихся 10 класса.
Цель экзамена: проверка уровня предметной компетентности учащихся 10 класса
по математике за курс 10 класса в рамках проведения промежуточной аттестации.
Требования, предъявляемые к знаниям и умениям учащихся на экзамене:
- знать основные тригонометрические формулы, и уметь применять их для
преобразования выражений;
- находить значение тригонометрических функций по известному значению одной из них;
- знать формулы корней тригонометрических уравнений и уметь применять их для решения тригонометрических уравнений;
- уметь решать показательные уравнения;
- знать основные свойства логарифмов, и уметь применять их для преобразования выражений;
- знать взаимное расположение прямых и плоскостей в пространстве;
- уметь вычислять значение выражения с корнями,
- уметь находить площадь поверхности в многогранниках.
Форма экзамена: письменно, по контрольно-измерительным материалам.
Количество вариантов - 3.
Время выполнения экзаменационной работы: 1 урок
Структура экзаменационной работы:
Каждый вариант экзаменационной работы содержит 2 части.
1 часть содержит 5 заданий по алгебре и началам анализа и 1 задание по геометрии базового уровня сложности. Эти задания направлены на проверку усвоения основных свойств, понятий, владения основными алгоритмами, умения решать простейшие уравнения.
2 часть содержит 1 задание по алгебре и началам анализа и 1 задание по геометрии повышенного и высокого уровня сложности. При выполнении этих заданий проверяется умение учащихся применять знания в несколько измененной ситуации. В заданиях второй части учащиеся должны записать решения и обосновать их.
Ответы к промежуточной аттестации по математике за курс 10 класса
| №№ заданий | Вариант №1.
| Вариант №2. | Вариант №3. | Вариант №4.
|
| Часть I |
|
| А1 | 7 | 9 | 8 | 12 |
| А2 | 2 | 3 | 0 | 4 |
| А3 | 0,5 | ─ 1,5 | 1,5 | 0,5 |
| А4 | ─ 2 | ─ 0,5 | ─ 0,5 | ─ 0,2 |
| А5 | 4 | 3 | 2 | 4 |
| В1 | ─ 0,75 | ─ 2 | 5 | 0,75 |
| Часть II |
|
| С1 | а) 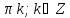 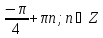
б) ─ 2π; ─  ; ─ π; ─ ; ─ π; ─  . . | а) 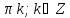 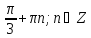
б) 2π;  . . | а)  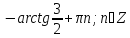
б) 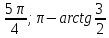 | а) 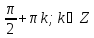
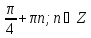
б) ─  ; ─ ; ─  . . |
|
С2 |
96 |
10 |
84 |
360 |
Критерии оценивания работы:
Каждое задание 1 части оценивается в один балл, задания 2 части оцениваются в 2 балла.
| Отметка
| Количество баллов |
| «5» | 9-10 |
| «4» | 7-8 |
| «3» | 4-6 |
| «2» | 0-3 |
Дата: «15» __апреля__ 2017 г.
Учитель: ________________ / Медведева И.Ю. /
Промежуточная аттестация по математике за курс 10 класса.
Вариант 1.
А1. Вычислите значение выражения  .
.
А2. Вычислите 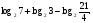
А3. Вычислите sin 210º + tg 2250.
А4. Найдите корень уравнения 21-3х = 128.
А5. Точки А,В, С и Д не лежат в одной плоскости.
Выберите верное утверждение:
1) прямая АВ параллельна прямой СД;
2) прямая АВ пересекает прямую СД;
3) прямая АС пересекает прямую ВД;
4) прямые АС и ВД – скрещиваются.
В1. Найдите tg x, если cosx =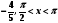
Для записи ответа на задание С1-С2 используйте лист
со штампом СОШ №59. Запишите обоснованное решение.
С1.а) Решите уравнение sin2х +2sin2 х =0.
б) Найдите все корни этого уравнения, принадлежащие
отрезку [-2π; -π/2].
С2. Найдите площадь поверхности правильной
четырехугольной пирамиды, стороны основания
которой равны 6 и высота равна 4.

Промежуточная аттестация по математике за курс 10 класса.
Вариант 2.
А1. Вычислите значение выражения  .
.
А2. Вычислите 
А3. Вычислите cos 120º+ tg 3150.
А4. Найдите корень уравнения 32-4х = 81.
А5. Точки А,В, С и Д лежат в одной плоскости. Выберите утверждение, которое не может быть верным:
1) прямая АВ параллельна прямой СД;
2) прямая АВ пересекает прямую СД;
3) прямые АС и ВД – скрещиваются;
4) прямая АС пересекает прямую ВД.
В1. Найдите tg x, если cos x =  ,
, 
Для записи ответа на задание С1-С2 используйте лист
со штампом ГБОУ СОШ №59. Запишите обоснованное решение.
С1.а) Решите уравнение 2sin2 х -  sin2х =0.
sin2х =0.
б) Найдите все корни этого уравнения, принадлежащие
отрезку [3π/2;3π].
С2. В правильной треугольной пирамиде SABC точка M– середина ребра AB, S – вершина. Известно, что BC=3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM. 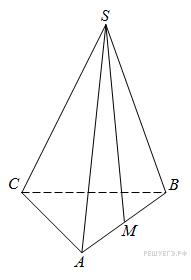
Промежуточная аттестация по математике за курс 10 класса.
Вариант 3.
А1. Вычислите значение выражения  *
*  + 2.
+ 2.
А2. Вычислите 2 +
+  .
.
А3. Вычислите cos 300º - tg 135º.
А4. Найдите корень уравнения 53-2х = 625.
А5. Точки А,В, С и Д лежат в одной плоскости. Выберите утверждение, которое не может быть верным:
1) прямая АВ параллельна прямой СД;
2) прямые АС и ВД – скрещиваются;.
3) прямая АС пересекает прямую ВД;
4) прямая АВ пересекает прямую СД.
В1. Найдите
Для записи ответа на задание С1-С2 используйте лист
со штампом ГБОУ СОШ №59. Запишите обоснованное решение.
С1. а) Решите уравнение
б) Укажите все корни этого уравнения, принадлежащие
отрезку 
С2. Стороны основания правильной четырёхугольной пирамиды равны 6, боковые рёбра равны 5. Найдите площадь поверхности этой пирамиды.

Повторная аттестация по математике за курс 10 класса.
Вариант 4.
А1. Вычислите значение выражения  .
.
А2. Вычислите  - 2
- 2 +
+  .
.
А3. Вычислите sin 210º - tg 3150.
А4. Найдите корень уравнения 24-5х = 32.
А5. Точки А, В, С и D не лежат в одной плоскости.
Выберите верное утверждение:
1) прямая АВ пересекает прямую СD;
2) прямая АВ параллельна прямой СD;
3) прямая ВС пересекает прямую АD;
4) прямые АС и ВD – скрещиваются.
В1. Найдите tg x, если
Для записи ответа на задание С1-С2 используйте лист
со штампом СОШ №59. Запишите обоснованное решение.
С1.а) Решите уравнение sin2х - 2cos2 х =0.
б) Найдите все корни этого уравнения, принадлежащие
отрезку [-2π; -π].
С2. Найдите площадь поверхности правильной
четырехугольной пирамиды, стороны основания
которой равны 10 и высота равна 12.

Бланк ответов №1
 Фамилия, имя
Фамилия, имя
класс 10
 Номер варианта
Номер варианта
Решение заданий А1 – В1 на черновике,
краткое, свой ответ запишите в бланк ответов
Ответом на задания А1-А5 должно быть некоторое целое число или
число, записанное в виде десятичной дроби. Это число надо записать
в бланк ответов №1 справа от номера задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа и
запятую в записи десятичной дроби пишите в отдельной клеточке
в соответствии с приведенными в бланке образцами.
Решение заданий С1-С2 записать подробно на листе
со штампом обр.учреждения







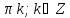
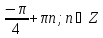
 ; ─ π; ─
; ─ π; ─  .
.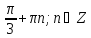
 .
.
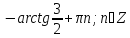
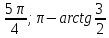
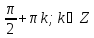
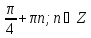
 ; ─
; ─  .
. .
.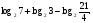
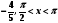

 .
.
 ,
, 
 sin2х =0.
sin2х =0.
 *
* 









