«Простые и составные числа» (5 класс)

Открытый урок-путешествие по теме:

«Простые и составные числа» (5 класс)

Цели и задачи:

Обучающие:

• отработка навыков умений систематизировать, обобщать знания о простых и составных числах;

• нахождении НОД и НОК и разложение числа на простые множители;

Развивающие:

• развивать логическое мышление;

• формировать навыки работы с дополнительным материалом;

• развивать познавательный интерес, интеллектуальные и творческие способности учащихся;

• формировать информационную культуру, овладение навыками поиска и анализа  информации;

Воспитательные:

• воспитывать уважительное отношение друг к другу;

• воспитывать аккуратность, эстетический вкус;

• обучать самостоятельной деятельности по овладению знаниями;   

• формировать осознанные мотивы учения, самосовершенствования, самовоспитания;

• воспитывать целеустремленность и настойчивость в достижении цели.

Оборудование:

• Мультимедиа проектор.

• Презентация к уроку.

Ход урока

1. Организационный момент

Ребята, сегодня у нас необычный урок математики, сегодня мы с вами совершим путешествие в галактику Простых и составных чисел.

2. Основная часть урока

Мы отправляемся в путешествие на звездолёте. Усаживайтесь удобнее. Погода за бортом отличная, настроение пассажиров приличное. Во время путешествия вам придётся выполнить ряд заданий, за правильно выполненное задание вы получите звезду. Тому, кто наберёт больше всех звёзд, присуждается звание «Лучший математик».

Счастливого всем полёта!

Мы приближаемся к созвездию с необычным названием Эратосфен.

На борту звездолёта известный экскурсовод, из его рассказа вы узнаете, почему так странно названо это созвездие.

Сообщение ученика о «решете Эратосфена».

Эратосфен Киренский ( 276 – 194 год до н.э.).

Один из самых разносторонних ученых античности. Особенно прославили Эратосфена труды по астрономии, географии и математике, однако он успешно трудился и в области филологии, поэзии, музыки и философии.

Имя Эратосфена вошло в науку в связи с методом отыскания простых чисел.

Ученик рассказывает последовательно, как составлялась таблица.

Посмотрим как применялся этот способ для поиска всех простых чисел, меньших 50.

1. Выписываем все числа от 1 до 50.

2. Вычеркиваем 1.

3. Затем последовательно вычеркиваем числа кратные 2, 3, 5, 7, и т.д. Каждый раз вычеркивались кратные первого « уцелевшего» числа.

В древности греки писали на покрытых воском табличках острой палочкой – стилем, а числа не вычеркивали, а выкалывали стилем, таблица в конце вычислений напоминала решето. С тех пор метод Эратосфена называют «решето Эратосфена»: в этом решете простые числа « отсеиваются» от остальных.

Учитель: Теперь вы знаете, в честь кого названо это созвездие. Продолжим путешествие.

Мы совершаем посадку на созвездие Решай – ка .

Жители этой планеты очень любят решать интересные задачи. Общество любителей математики предлагает и вам решить несколько задач.

I. Устная работа

№ 1.

Даны числа: 1, 2, 3, 7, 12, 15, 20, 28, 31, 43.

На сколько групп можно разбить эти числа и по какому признаку?

Группы:

- один делитель (1);

- два делителя (2, 3, 7, 31, 43);

- больше двух делителей (12, 15, 20, 28).

Как называются числам, которые имеют два делителя? Как называются числа, которые имеют больше двух делителей? А будет ли единица простым числом? Будет ли единица составным числом?

№ 2. С помощью таблицы простых чисел определите, является ли простым число: 47, 69,127, 301, 447, 517, 673, 879.

II Письменные задания
№ 3. ( у доски)

Маша испекла 30 кексов. Сколько друзей может пригласить Маша, чтобы каждому гостю досталось одинаковое количество кексов?

Решение. Надо найти делители числа 30. 30: 1; 2; 3; 5; 6; 10; 15; 30.

Ответ: Маша может пригласить 1 или 2, или 3 или 5 или 6 или 10 или 15 или 30 друзей.

№ 4. ( пишем и проговариваем)

Найдите делители чисел: 50, 7, 829, 31, 24, 10, 21, 5, 100.

Решение:

50: 1; 2; 5; 10; 25; 50.

7: 1; 7.

829: 1; 829.

31: 1; 31.

24: 1; 2; 3; 4; 6; 8; 12; 24.

10: 1; 2; 5; 10.

21: 1; 3; 7; 21.

5: 1; 5.

100: 1; 2; 4; 5; 10; 20; 25; 50; 100.

№ 5. (работа по вариантам, по одному человеку от каждого варианта у доски).

Найти:

I НОД ( 48, 28); НОК (12, 15, 20)

II НОД ( 42, 36); НОК (10, 16, 40)

III НОД ( 84, 28); НОК (18, 12, 30)

Решение:

I 48: 1; 2; 3; 4; 6; 8; 12; 16; 24;48. 28: 1; 2; 4; 7; 14; 28. НОД ( 48, 28) = 4

12: 12; 24; 36; 48; 60 72. 15: 15; 30; 45; 60; 75. 20: 20; 40; 60.

НОК (12, 15,20) = 60

II 42: 1; 2; 3; 6; 7; 14; 21; 42. 36: 1; 2; 3; 4; 6; 9; 12; 18; 36.

НОД ( 42, 36) = 6

10: 10; 20; 30; 40; 50; 60; 70; 80 16: 16; 32; 48; 64; 80

40: 40; 80; 120 НОК (10, 16, 40) = 80

III 84: 1; 2; 3; 4; 7; 12; 21; 28; 42; 84. 28: 1; 2; 4; 7; 14; 28.

НОД ( 84, 28) = 4;

15: 15; 30; 45; 60 12: 12; 24; 36; 48; 60 30: 30; 60

НОК (15, 12, 30) = 60

№ 7. Какое число разложено на простые множители?

2 * 3² * 7 =126

2³ * 3 * 5 = 120

3² * 5 * 11 = 495

№ 8. Найдите х и запишите полученные результаты в порядке убывания.

5х + 3х = 720 ( х = 90) 12х – 5х = 560 ( х = 80)

6х + 3х = 900 ( х = 100) 10х – 5х + 2х = 490 ( х = 70)

100; 90; 80; 70.

- Что интересного можно сказать о полученном ряде чисел? Какое следующее число?

- Назовите из полученного ряда число, кратное 40 ( 80 ).

- Какое число из полученного ряда можно заменить произведением двух одинаковых множителей ? (100 = 10 * 10) . Разложите это число на простые множители. ( 100 = 2² * 5² )

Продолжаем путешествие.

Мы приближаемся к созвездию Сказка.

Здесь, ребята, мы вместе с вами покажем сказку. (У ребят соответствующие таблички с числами, они выходят по ходу сказки).

28 сентября число 28 решило пригласить в гости всех своих делителей, меньших, чем оно само. Кто пойдёт к нему в гости?

Когда все гости собрались, число 28 огорчилось и предложило, чтобы каждый из своих гостей привёл ещё своих делителей. Сколько придёт новых гостей?

Чтобы утешить число 28, его гости соединились знаком «+». И, что же получилось?

Сумма оказалась равной самому числу 28!

Всякое число, которое равно сумме своих меньших делителей, называется совершенным.

28 – совершенное число. Совершенные числа встречаются очень редко: среди чисел до миллиона только четыре совершенных.Число 28 – единственное двузначное совершенное число, есть только одно трёхзначное совершенное число – 496. Число 8128 – четвертое совершенное число.

Проверьте, что число 496 совершенное, и найдите однозначное совершенное число. (однозначное совершенное число 6).

496: 1; 2; 4; 8; 16; 31; 62; 124; 248; 496.

1+2+4+8+16+31+62+124+248= 496

Учитель: Вы, ребята, все устали

Много думали, считали

Отдохнуть уже пора.

Следующее созвездие «Спортивное»

 Физкультминутка.  (Ученики повторяют движения за учителем).

Мы все вместе улыбнемся,

Подмигнем слегка друг другу,

Вправо, влево повернемся ( повороты влево- вправо)

И кивнем затем по кругу. (наклоны влево-вправо)

Все идеи победили,

Вверх взметнулись наши руки. ( поднимают руки вверх- вниз)

Груз забот с себя стряхнули

И продолжим путь науки. ( встряхнули кистями рук).

На нашем пути созвездие «Научно - исследовательское».

Интерес математиков к простым числам был огромен, начиная с древних времен. Само понятие простого числа было введено древнегреческим ученым Пифагором в 4 веке до н. э. В 3 веке до н.э. Евклид доказал, что простых чисел бесконечно много. Первым глубокие исследования о том как разбросаны простые числа среди остальных натуральных чисел, получил великий русский математик Пафнутий Львович Чебышев, основатель и руководитель математических исследований XIX века.

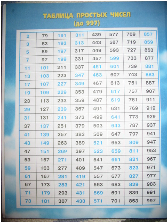
Давайте посмотрим в таблицу простых чисел.

?? Некоторые числа выделены другим цветом. Что можно сказать про эти числа. (Среди них одно простое четное число 2, а остальные нечетные. 2 и 3 последовательные натуральные числа, наименьшие простые – такая пара единственная, где одно число четное, а другое нечетное.)

Определение: Два последовательных нечетных простых числа, каждое из которых отличается на 2 называются числами близнецами, например: 11и 13; 17 и 19; 29 и 31.

Задание. Посмотрите в таблицу простых чисел и найдите еще числа-близнецы. ( учащихся разбить на группы по 4 человека). Посчитайте, сколько пар чисел – близнецов в каждой сотне.

(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), 8

(101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), 7

(227, 229), (239, 241), (269, 271), (281, 283), 4

(311, 313), (347, 349), 3

(419, 421), (431, 433), (461, 463), 3

(521, 523), (569, 571), (599, 601), 3

(617, 619), (641, 643), (659, 661), 3

(809, 811), (821, 823), (827, 829), (857, 859), (881, 883) 5

???? Можно ли сделать вывод о закономерности расположения чисел – близнецов в таблице простых чисел.

До сих пор математики не знают формулы, с помощью которой можно получить только простые числа.

1949 и 1951- годы близнецы.

Ближайшие годы близнецы- 2027 и 2029 годы.

Найдены гигантские числа-близнецы: 10016957 и 10016959.

Числа 10999949 и 10999951 – самые большие, ныне известные, числа-близнецы. 

Подведение итогов.

Пора возвращаться домой. Я думаю, путешествие прошло с большой пользой для вас. Что же нового мы узнали? Да, мы узнали, какие числа называются совершенным и числами - близнецами.

Множество натуральных чисел можно сравнить со звездами на небе.

И в заключении   мне хочется зачитать отрывок из книги Д. С. Фаермарка «Задача пришла с картины».

В бесконечном множестве натуральных чисел, так же как среди звезд Вселенной, выделяются отдельные числа и целые их «созвездия» удивительной красоты, числа с необыкновенными свойствами и своеобразной, только им присущей гармонией. Надо только уметь увидеть эти числа, заметить их свойства. Всмотритесь в натуральный ряд чисел – и вы найдете в нем много удивительного и диковинного, забавного и серьезного, неожиданного и курьезного. Видит тот, кто смотрит. Ведь люди и в летнюю звездную ночь не заметят… сияние Полярной звезды, если не направят свой взор в безоблачную высь.

Домашнее задание.

Проверить, что число 8128 – совершенное.

Итог урока.

Урок по математике в 5 классе по теме «Простые и составные числа»

Подготовила и провела учитель математики

МОУ «Средняя общеобразовательная школа № 35

им. К. Д. Воробьева» г. Курска

Чуйкова С. Ю.

Курск – 2011