ПРАКТИЧЕСКОЕ пособие
по теме:
«ЗАДАЧИ НА Проценты»
Аннотация
Данное практическое пособие посвящено теме «Проценты». Разработка пособия актуальна тем, что тема «Проценты» изучается непродолжительное время в школьном курсе, но задания по процентам включаются в материалы итоговой аттестации за курс основной школы, в КИМы и ЕГЭ. Понимание процентов и умение производить процентные расчеты в современной жизни необходимы каждому человеку. В данном пособии дается краткое определение понятия «Процент», рассматриваются основные способы решения типовых задач на проценты, рассматриваются задачи с практическим содержанием, которые связаны с применением процентных вычислений в повседневной жизни. Также дается материал для самостоятельного рассмотрения, предлагаемые задачи различны по уровню сложности.
Содержание
Аннотация
Содержание
Введение
I. Понятие «Процент» и основные способы решения задач на проценты
II. Типовые задачи на проценты
2.1. Задачи на проценты в торговле
2.2. Задачи на концентрацию, смеси и сплавы
2.2.1. Решение задач стандартным способом
2.2.2. Решение задач с помощью «квадрата Пирсона»
2.3. Задачи на проценты в экологии
2.4. Задачи на проценты в банковской сфере
2.4.1. Простые банковские проценты
2.4.2. Сложные банковские проценты III. Задания для самостоятельного рассмотрения
IV. Список использованных источников
Введение
Математика в настоящее время все шире проникая в повседневную жизнь и обиходный язык, все более внедряется в традиционно далекие от нее области. Интенсивная математизация различных областей человеческой деятельности особенно усилилась с внедрением современных информационных технологий, требующих математической грамотности человека буквально на каждом рабочем месте. Проценты – одно из математических понятий, которые часто встречаются в повседневной жизни.
Слово «процент» происходит от латинского pro centum, что буквально означает «на сотню», «со ста» или «за сотню». В популярной литературе возникновение этого термина связывается с внедрением в Европе десятичной системы счисления в XV в. Но идея выражения частей целого постоянно в одних и тех же величинах, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти». Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. По-видимому, процент возник в Европе вместе с ростовщичеством. Есть мнение, что понятие процент ввел бельгийский ученый Симон Стевин. В 1584 г. он опубликовал таблицы процентов. Употребление термина «процент» в России начинается в конце XVIII в. Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Интересно происхождение обозначения процента. Существует версия, что знак % происходит от итальянского pro cento (сто), которое в процентных расчетах часто сокращенно писалось cto. Отсюда путем дальнейшего сокращения в скорописи буква t превратилась в наклонную черту (/), возник современный знак процента. Также есть предположение, что знак % возник в результате опечатки. В Париже в 1685 г. была напечатана книга руководство по коммерческой арифметике, где по ошибке наборщик напечатал знак %.
В настоящее время понимание процентов и умение производить процентные расчеты необходимо каждому человеку, это способствует «вхождению» в современную информационно-экономическую среду и, в конечном счете, облегчает социализацию. Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки невозможны без умения производить несложные процентные вычисления. Любой человек должен уметь свободно решать задачи, предлагаемые самой жизнью, уметь просчитать различные предложения магазинов, кредитных отделов и различных банков и выбрать наиболее выгодные.
Поэтому цель данного практического пособия состоит в практическом изучении темы «Процент».
Для достижения поставленной цели, необходимо решить следующие задачи:
-
Дать определение понятию «Процент».
-
Изучить основные способы решения задач на проценты.
-
Изучить типы задач на проценты.
-
Составить и решить различные задачи по теме исследования
I. Понятие «Процент» и основные способы решения задач на проценты
Что такое проценты в математике? Нужно запомнить – что такое один процент. Это понятие - и есть главный ключ к решению задач на проценты, да и к работе с процентами вообще.
Один процент – это одна сотая часть какого-то числа.
Существует три основных типа задач на проценты:
| Задача 1. | Найти указанный процент от заданного числа.
Заданное число делится на 100 процентов, а затем произведение умножается на указанное число процентов. |
| Пример .
Решение | Вклад в банке имеет годовой прирост 21%. Начальная сумма вклада равнялась 60000 руб. На сколько рублей возрастёт сумма вклада в конце года? 60000 : 100∙ 21 = 21600 |
| Задача 2. | Найти число по заданному другому числу и его величине в процентах от искомого числа. Заданное число делится на его процентное выражение и результат умножается на 100. |
| Пример .
Решение | Зарплата в январе равнялась 14600 руб., что составило 36,5% от годовой зарплаты. Какова была годовая зарплата? 14600 : 36,5 ∙ 100 = 40000 рублей
|
| Задача 3. | Найти процентное выражение одного числа от другого. Меньшее число делится на большее и результат умножается на 100. |
| Пример .
Решение | Завод произвёл за год 100000 автомобилей, а в следующем году – только 41000 автомобилей. Сколько процентов это составило по отношению к выпуску предыдущего года?
41000 : 100000 ∙ 100 = 41%
|
II. Типы задач на проценты
2.1. Задачи на проценты, используемые в торговле
Задача № 1. Цена 1 кг конфет в магазине первоначально составляла 71 рублей. C декабря месяца цена сначала поднялась на 15%, а потом понизилась на 8%, затем снова поднялась на 13%. Какова конечная цена 1 кг конфет?
Решение:
I действие: 71 руб. - 100%
х - 15%
x= (71·15):100 ≈ 10,7 (руб.)
71 + 10,7 = 81,7 (руб.) – цена 1 кг конфет после повышения цены.
II действие: 81,7 – 100%
х - 8%
x= (81,7·8):100 ≈ 6,5 (руб.)
81,7 – 6,5 = 75,2 (руб.) - цена 1 кг конфет после понижения цены.
III действие: 75,2 – 100%
х - 13%
x = (75,2·13):100 ≈ 9,8 (руб.)
75,2 + 9,8 = 85 (руб.) - цена 1 кг конфет после повышения цены.
Ответ: цена 1 кг конфет стала 85 рублей.
Задача № 2. Книга «Математика» стоила 360 рублей. В ноябре цена книги «Математика» была снижена на 15%, а в декабре еще на 10%. Какой стала стоимость книги «Математика» в декабре?
Решение:
1) Стоимость книги «Математики» в ноябре составляла 85 % от 360 руб., т. е. 360·0,85 = 306(руб.).
2) Второе снижение цены происходило по отношению к новой цене книги «Математика»; теперь следует искать 90 % от 306 руб., т. е.
306·0,9 = 275,4 (руб.)
Ответ: 275 рублей 40 копеек.
Задача № 3. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 900 рублей после повышения цены на 10%?
Решение: Находим 10% от 40
10:100 ·40 = 0,1·40 = 4 руб.
40+4 = 44 (руб.)
Новая цена тетради составит 44 рубля. 900 : 44≈20,45, т.е. 20 тетрадей.
Ответ: на 900 рублей можно купить 20 тетрадей.
Задача № 4. Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
Решение: Запомним важное правило: за 100% принимается та величина, с которой мы сравниваем.
Цена была повышена на 16% по сравнению с чем? — с прежней ценой. Значит, прежняя цена — это 100%, новая цена — 100%+16% = 116%. Составляем пропорцию:
100% - х руб.
116% - 3480 руб.
Составляем и решаем уравнение 100 ·3480 = 116 · х
х = 100 ·3480:116
х = 3000.
Ответ: 3000 рублей стоил чайник до повышения цены.
Задача № 5. При покупке ребенку новых лыж с ботинками родителям пришлось заплатить на 35 % больше, чем два года назад, причем лыжи подорожали с тех пор на 20 %, а ботинки — на 70 %. Сколько процентов от стоимости лыж с ботинками составляла два года назад стоимость лыж?
| | Стоимость лыж (руб.) | Стоимость ботинок (руб.) | Стоимость лыж и ботинок вместе (руб.) |
| Два года назад | х | у | х + у |
| Сейчас | х + 0,2х = 1,2х | у + 0,7у = 1,7у | (х + у) + 0,35(х + у) |
Уравнение:
1,2х + 1,7у = (х + у) + 0,35(х + у)
1,2х + 1,7у = х + у + 0,35х + 0,35у
1,2х + 1,7у = 1,35х + 1,35у
1,7у – 1,35у = 1,35х – 1,2х
0,35у = 0,15х
х = 0,35у : 0,15
х = 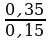 у
у
х = 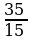 у
у
х = 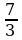 у
у
��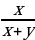
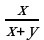 · 100% =
· 100% = 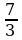 у : (
у : (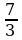 у + у) ·100% =
у + у) ·100% = 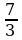 у :
у : 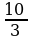 у · 100% =
у · 100% =
=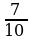 · 100% = 70%
· 100% = 70%
Ответ: 70% от стоимости лыж с ботинками составляла два года назад стоимость лыж.
Задачи для закрепления материала.
-
Цену на пальто снизили на 30%, затем новую цену повысили на 30%. Как изменилась цена на пальто?
-
Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10% за каждый месяц. На сколько процентов выросли цены за 3 месяца?
-
Антикварный магазин приобрел старинный кинжал за 30 тысяч рублей. И выставил его на продажу, повысив цену на 60%. Но этот кинжал был продан лишь через неделю, когда магазин снизил его новую цену на 20%. Какую прибыль получил магазин при продаже старинного кинжала?
2.2. Задачи на концентрацию, смеси и сплавы
2.2.1. Решение задач стандартным способом
Задача № 1. Сколько килограммов сахара в 10 килограммах сиропа, если процентное содержание сахара составляет 15%?
Решение:
10 · 0,15 = 1,5 (кг) соли.
Ответ: 1,5 кг.
Процентное содержание вещества в растворе (например, 15%), иногда называют процентным раствором, например, 15%-й сиропа.
Задача № 2. Сплав содержит 10 кг олова и 15 кг меди. Каково процентное содержание олова и меди в сплаве?
Решение: Процентное содержание вещества в сплаве – это часть, которую составляет вес данного вещества от веса всего сплава.
1) 10 + 15 = 25 (кг) – сплав;
2) 10:25 · 100% = 40% – процентное содержание олова в сплаве;
3) 15:25 · 100% = 60% – процентное содержание меди в сплаве;
Ответ: 40%, 60%.
Задача № 3. К 15 л 10%-ого раствора уксуса добавили 5%-ый раствор уксуса и получили 8%-ый раствор. Какое количество литров 5%-ого раствора добавили?
Решение. Пусть добавили х л 5%-ого уксусного раствора. Тогда нового раствора стало
(15 + х) л, в котором содержится 0,8 . (15 + х) л уксуса. В 15 л 10%-ого раствора содержится 15 . 0,1 = 1,5 (л) уксуса, в х л 5%-ого раствора содержится 0,05х (л) уксуса.
Составим уравнение.
1,5 + 0,05х = 0,08 . (15 + х)
1,5+0,05х=1,2+0,08х
- 0,03х= - 0,3
х = 10.
Ответ: добавили 10 л 5%-ого раствора.
Задача № 4. 5 литров сливок с содержанием жира 35% смешали с 4 литрами 20%-ых сливок и к смеси добавили 1 литр чистой воды. Какой жирности получилась смесь?
Решение. 0,35·5+0,2·4=р·(5+4+1), откуда р=0,255, что составляет 25,5%
Ответ: 25,5%
Задача № 5. Имеются два слитка сплава золота с медью. Первый слиток содержит 230 г золота и 20 г меди, а второй слиток – 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором оказалось 84 % золота. Определить массу (в граммах) куска, взятого от первого слитка.
Решение. Определим процентное содержание золота в обоих слитках.
1) 230+20=250(г) - масса 1 слитка,
2) 230:250=0,92 (92%) - процентное содержание золота в 1 слитке.
3) 240+60=300(г) - масса 2 слитка,
4) 240:300=0,8 (80%)- процентное содержание золота во 2 слитке.
Пусть х масса куска, взятого от 1 слитка, (300-х)- масса куска, взятого от 2 слитка, получим уравнение:
0,92х+0,8(300-х)=0,84·300
0,92х+240-0,8х=252
0,12х=12
х=100
Ответ: 100 г.
2.2.2. Решение задач с помощью «Квадрата Пирсона»
Данный способ решения задач на проценты был предложен английским математиком Карлом Пирсоном, и заключается в следующем: чертится квадрат и проводятся диагонали. В левом верхнем углу ставят больший показатель крепости (А), в левом нижнем углу ставят меньший показатель крепости (В), на пересечении диагоналей ставят требуемый показатель крепости (С). В правом нижнем углу после вычитания из А С ставят У, а в правом верхнем углу после вычитания из С В получают Х
А – С = У
С – В = Х.
Надо взять Х частей с концентрацией А и У частей с концентрацией В, чтобы получить смесь с концентрацией С.
Одним из преимуществ этого способа является то, что он доступен ученикам, которые не умеют решать уравнения. Также квадрат Пирсона очень полезен для домохозяек, чтобы получать нужную концентрацию уксуса или сиропа. Недостатком данного способа можно назвать, что его нельзя применять при решении задач на смешивание трех и более растворов.
Задача 1. Один раствор содержит 20% соли, а второй – 70%. Сколько нужно граммов первого и второго раствора взять, чтобы получить 100г. 50%-го солевого раствора?
Решение.
Решим задачу с помощью квадрата Пирсона.



С
А Х 70 30 3



50
В У
2
20 20
Значит, 100 г. смеси составляет 5 частей.
Одна часть – 100/(3+2) = 20(г),
70%-ый раствор – 20*3=60 (г),
20%-ый раствор – 20*2=40 (г).
Ответ: 20% -го 40 г, 70%-го 60г.
Задачи для закрепления материала.
-
При смешивании 5%-ного раствора кислоты с 40%-ным раствором кислоты получили 140 г 30%-ного раствора. Сколько граммов каждого раствора было для этого взято?
-
Смешали 4 литра 15%-ого водного раствора некоторого вещества с 6 литрами 25%-ого водного раствора того же вещества. Сколько процентов составляет концентрация полученного раствора?
-
Хозяйке для засолки огурцов необходимо получить 6%-ый раствор уксусной кислоты, используя 70%-ый раствор уксусной кислоты и воду. Сколько необходимо взять 70%-ого раствора и воды, чтобы получить 700 г раствора необходимой концентрации?
2.3. Задачи на проценты в экологии
Задача № 1. В 1 м2 городского воздуха содержится около 5000 микробов. А в 1 м2 лесного массива - около 500 микробов. Какой процент микробы 1м2 лесного массива составляют от микробов 1м2 городского воздуха?
Решение:
500:5000 = 0,1 = 10%.
Ответ: 10%
Задача № 2. В 2013 году было посажено 250 га кукурузы, а в 2014 году и в 2015 году площадь кукурузы составила 72% от площади, засаженной в 2013 году. Сколько гектаров кукурузы было посажено в 2014 и 2015 году?
Решение:
|
| га | % |
| 2013 г. | 250 | 100 |
| 2014-15 гг. | х | 72 |
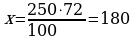 (га)
(га)
Ответ: по 180 га.
Задача № 3. В городе через канализационную очистительную систему (КОС) в 2014 году поступало 2840 тонн загрязняющих веществ. Из них 23% проходят недостаточную очистку, а 7% остаются без очистки. Какое количество загрязняющих веществ возвращается в природные водоемы практически без очистки?
Решение:
1) 23% +7% = 30 %
2) 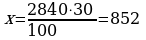 (т)
(т)
Ответ: 852 тонны.
Задача № 4. Сколько тонн отходов от автотранспорта было выброшено в 2013 году в атмосферу города, если угарный газ составил 10300 тонн, оксид азота составил 13% от величины угарного газа, оксиды серы составили 3,5% от величины угарного газа?
Решение:
1)10300:100·13 =1339 (т)
2)10300:100·3,5 =360,5 (т)
3)10300+1339+360,5= 11999,5 (т)
Ответ: 11999,5 тонн.
Задача № 5. В 2013 году было вырублено 10 га леса, в 2014 — в два раза больше, в 2015 году — в 7 раз больше, чем в 2014 году. На сколько процентов увеличилась площадь вырубаемого леса?
Решение:
-
10 · 2 = 20(га) – 2014 году
-
20 · 7 = 140(га) – вырублено в 2015 году
-
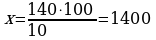 %
%
-
1400% – 100% = 1300 %
Ответ: на 1300%.
Задачи для закрепления материала.
-
На острове Мадагаскар из 28 местных видов птиц вымерло 24. Определите этот, самый высокий в мире, процент исчезнувших птиц.
-
Влажность воздуха к полудню по сравнению с утренней снизилась на 12%, а затем повысилась на 5% по сравнению с полуднем. Сколько процентов от утренней влажности составляет влажность воздуха к вечеру и на сколько процентов она снизилась?
-
В мире ежегодно добывается 1600 млн. м3 древесины, около 20% всей древесины идет на топливо. Сколько кубических метров древесины сжигается?
2.4. Задачи на проценты в банковской сфере
2.4.1. Простые банковские проценты
Если проценты начисляют на постоянную сумму, это означает, что начисляют простые проценты.
S = a * (1 + n * P/100) – формула простых процентов,
Где S – искомая сумма, n – период, P – начисляемый процент.
Задача №1. Вкладчик положил в банк 50000 рублей. Банк начисляет ежемесячно 3 % дохода на сумму первоначального вклада. Какая сумма окажется на счете вкладчика через 16 месяцев?
Решение:
S = 50000 *(1 + 16 * 3/100) = 74000.
Ответ: На вкладе через 16 месяцев окажется 74000рублей.
Задача № 2. Каким должен быть начальный вклад, чтобы при ставке 4% в месяц увеличился за 8 месяцев до 33000 рублей?
Решение:
S0 · (1+8 ·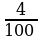 ) = 33000,
) = 33000,
S0 = 33 000 · 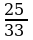 = 25000 рублей
= 25000 рублей
Ответ: начальный вклад должен быть 25000 рублей.
2.4.2. Сложные банковские проценты
Если процент начисляют на изменяющуюся сумму – это сложные проценты.
S = a * (1 + n * P/100)n – формула сложных процентов.
Задача №1. Вкладчик положил в банк 40 000р. Банк начисляет ежемесячно 5% дохода на сумму вклада, находящуюся на счете вкладчика к началу месяца. Какой доход получит вкладчик за 3 месяца?
Решение:
За первый месяц доход составит 0,05*40000 = 2000 (р), и на вкладе окажется 42000р.
За второй месяц доход составит 0,05*42000 = 2100 (р), и на вкладе окажется 44100р.
За третий месяц доход составит 0,05*44100 = 2205 (р), и на вкладе окажется 46305р.
Тогда доход за 3 месяца составит 46305-40000=6305р.
Ответ: Доход составит 6305р.
Задача № 2. На банковский счет было положено 10 тысяч рублей. После того, как деньги пролежали один год, со счета сняли 1 тысячу рублей. Еще через год на счету стало 11 тысяч рублей. Какой процент годовых начисляет банк?
Решение:
Пусть банк начисляет р% годовых.
1) Сумма в 10000 рублей, положенная на банковский счет под р% годовых, через год возрастет до величины
10000 + 0,01p ·10000 = 10000 + 100р руб.
Когда со счета снимут 1000 руб., там останется 9000 + 100р руб.
2) Еще через год последняя величина за счет начисления процентов возрастет до величины 9000 + 100р + 0,01p(9000 + +100р) = р2 + 190р + 9000 руб.
По условию эта величина равна 11000 руб., поэтому имеем квадратное уравнение.
р 2 + 190р + 9000 = 11000;
р 2 + 190р - 2000 = 0
Решим это квадратное уравнение, используя теорему Виета, p1 = 10, p2 = -200.
Отрицательный корень не подходит.
Ответ: начислялось 10% годовых.
Задания для закрепления материала.
-
Сколько лежал в банке вклад 20000 рублей, если по ставке 20% годовых, он достиг величины 28000 рублей? Какие проценты применяются?
-
В банк положили 50000 рублей под 30% (при сложных процентах). Какова величина вклада через 4 года?
-
Михаил получил в подарок к своему 25-летию 2000 рублей и положил их в банк, который начисляет в качестве базовой ставки 7% в год. Какова будет сумма этого вклада к тому времени, когда Михаил уйдет на пенсию (в 65 лет)?
III. Задания для самостоятельного рассмотрения
-
Садовник для поливки роз смешивает удобрение «Росток» с 30%-ым содержанием калия и удобрение «Розочка» с 10%-ым содержанием калия и получает 600 граммов 15%-ого раствора. Сколько граммов каждого удобрения было взято?
-
На весенней распродаже в одном магазине шарф стоимостью 350 рублей уценили на 40%, а через неделю еще на 5%. В другом магазине шарф такой же стоимости уценили сразу на 45%. В каком магазине выгоднее купить этот шарф?
-
Кусок сплава меди и цинка в 36 кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?
-
В суровую зиму в лесу может погибнуть до 90% птиц. Если в лесу обитало 3400 птиц, то сколько птиц осталось?
-
Гектар лиственного леса вырабатывает 2 килограмма летучих защитных веществ, а гектар хвойного леса - 250% от этой величины. Сколько килограммов летучих защитных веществ вырабатывает гектар хвойного леса?
-
Через 6 лет нам нужны деньги в размере 20000 рублей при процентной ставке 20% (сложные проценты). Какую сумму нужно положить в банк?
-
Для получения 4 тонн нержавеющей стали, содержащей 20% хрома, на ОАО «Мечел» сплавили два сорта стали, содержащие соответственно 30% и 10% хрома. Определить массы каждой марки стали, взятой для сплавления.
-
Магазин закупает цветочные горшки по оптовой цене 140 рублей за штуку и продает с наценкой 25%. Какое наибольшее число таких горшков можно купить в этом магазине на 1300 рублей?
-
Вкладчик открыл счет в банке, внеся 2000 рублей на вклад, годовой доход по которому составляет 12%, и решил в течение 6 лет не брать процентные начисления. Какая сумма будет лежать на его счете через 6 лет?
-
В России лесом занято около 1 млрд. га, в том числе 80% всей площади – хвойными. Бором занято около 25%, а еловыми лесами – около 17% всей площади хвойных лесов. Сколько гектаров занимают бор и еловые леса?
-
Два банковских филиала обслуживали в прошлом году одинаковое количество клиентов. В этом году количество клиентов в первом филиале увеличилось на 150%, а во втором – в 2,5 раза. В каком филиале стало больше клиентов?
-
Флакон шампуня стоит 150 рублей. Какое наибольшее число флаконов можно купить на 700 рублей во время распродажи, когда скидка составляет 35%?
IV. Список использованных источников
-
Денищева Л.О., Бойченко Е.М., Глазков Ю.А., и др. Готовимся к Единому государственному экзамену. Математика. – М.: Дрофа, 2011;
-
Дорофеев Г.В., Седова Е.А. Процентные вычисления. 10-11 классы: учеб.-метод. пособие. – М.: Дрофа, 2003;
-
Никольский С.Н., Потапов М.К., Решетников Н.Н. Алгебра в 7 классе: методические материалы. – М.: Просвещение, 2014;
-
Рязановский А.р. Задачи на части и проценты//Математика в школе. - №1. 1992;
-
Шорина С.П. Обоснование старинного способа решения задач на смеси // Математика в школе. – 1997. - №6.








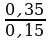 у
у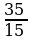 у
у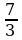 у
у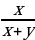
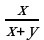 · 100% =
· 100% = 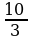 у · 100% =
у · 100% =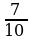 · 100% = 70%
· 100% = 70%





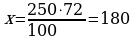 (га)
(га)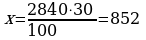 (т)
(т)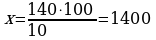 %
%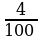 ) = 33000,
) = 33000, 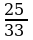 = 25000 рублей
= 25000 рублей

















