Пояснительная записка.
Рабочая программа по курсу «Алгебра и начала математического анализа» для 11 класса составлена на основе требований федерального компонента государственного образовательного стандарта среднего (полного) общего образования по математике Министерства образования и науки Российской Федерации (приказ Минобразования России от 5 марта 2004 года №1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования» с изменениями: приказ Министерства образования и науки Российской Федерации от 17.12.2010 №1897, приказ Минобрнауки России от 31.01.2012 года №69 «О внесении изменений в федеральный компонент государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования, утвержденный приказом Министерства образования Российской Федерации от 5марта2004 г. №1089») и в соответствии с базисным учебным планом школ РФ (приказ МО РФ от 09.03.2004 №1312 с изменениями: приказ Минобрнауки России от 01.02.2012 №74 «О внесении изменений в федеральный базисный учебный план и примерные учебные планы для образовательных учреждений Российской Федерации, реализующих программы общего образования, утвержденные приказом Министерства образования Российской Федерации от 9марта2004 г. №1312»), в соответствии с федеральным перечнем рекомендованных учебников на 2015-2016 года, на основе программы для общеобразовательных учреждений (Алгебра и начала математического анализа, 10-11 классы. Автор: Т. А. Бурмистрова. М., «Просвещение», 2010 год) и авторской программы по алгебре и началам математического анализа к учебнику для 11 класса общеобразовательных школ авторов Ю.М.Колягин, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин –М.: Просвещение, 2012 г. Указанная программа рассчитана на изучение предмета из расчета 3 часа в неделю (всего 102 часа). В базисном учебном плане МБОУ «Зубово-Полянская гимназия» на изучение алгебры и начал анализа в 11 классах общеобразовательного профиля отводится 2,5 часа в неделю: 2ч в первом полугодии, 3 ч во втором. Поэтому рабочая программа составлена исходя из базисного учебного плана.
В рабочую программу включены все рекомендуемые темы для 11 класса. Данная рабочая программа призвана обеспечить знания учащихся средней (полной) школы на базовом уровне.
На изучение предмета на базовом уровне согласно Федеральному базисному плану отводится 85 часов (2,5 часа в неделю): 2ч в первом полугодии, 3 ч во втором.
В примерную учебную программу по математике автора Т. А. Бурмистрова внесены следующие изменения и дополнения:
в распределение количества часов на изучение отдельно взятых тем
- уменьшено количество часов на изучение тем «Тригонометрические функции», «Производная и ее геометрический смысл», «Применение производной к исследованию функций», «Первообразная и интерграл», «Комбинаторика», «Элементы теории вероятностей» что объясняется степенью сложности учебного материал и значимости его для итоговой аттестации обучающихся.
Общая характеристика учебного предмета
При изучении курса алгебры на базовом уровне продолжаются и получают развитие содержательные линии: «Числа и вычисления», «Тождественные преобразования алгебраических выражений», «Функции», «Уравнения и неравенства», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа».
Изучение алгебры в старшей школе на базовом уровне направлено на достижение следующих целей:
- овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
- интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности в точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
- формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
В рамках указанных содержательных линий решаются следующие задачи:
- систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
- расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
- развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
- знакомство с основными идеями и методами математического анализа.
Содержание программы носит локальный (созданный для данного образовательного учреждения) и индивидуальный (разработанный учителем) характер. При проведении уроков используются разнообразные формы организации учебной деятельности (беседы, работы в группах, практикумы, игровые моменты, деловые игры и другие).
Образовательные и воспитательные задачи обучения математике должны решаться комплексно с учетом возрастных особенностей учащихся, специфики математики как науки и учебного предмета, определяющей ее роль и место в общей системе школьного обучения и воспитания.
Принципиальным положением организации математического образования в школе становится уровневая дифференциация обучения. Это означает, что, осваивая курс, одни школьники в своих результатах ограничиваются уровнем обязательной подготовки, зафиксированным в настоящей программе, другие в соответствии со своими склонностями достигают более высоких рубежей. При этом достижение уровня обязательной подготовки становится непременной обязанностью ученика в его учебной работе. В то же время каждый имеет право самостоятельно решить, ограничиться этим уровнем или же продвигаться дальше.
Учитывая разную степень подготовленности учащихся класса к освоению данной программы, следует всецело способствовать удовлетворению потребностей и запросов школьников, проявляющих интерес, склонности и способности к математике, а также имеющих сложности и трудности в обучении. Для первой категории предусмотрена разработка индивидуальных заданий и рекомендация дополнительной литературы с целью привлечения их к участию в олимпиадах, конкурсах. Для второй категории осуществлен индивидуальный подход, выражающийся в специальном подборе заданий по уровням сложности, в разработке опорных конспектов и схем для овладения тем или иным учебным материалом. Акцент в преподавании делается на практическое применение приобретённых навыков.
Межпредметные и межкурсовые связи широко используются при изучении тригонометрических функций. Например, в физике при изучении тем: «Колебания и волны», «Равномерное и неравномерное движения».
Рабочая программа составлена также с учетом специфики образовательного учреждения.
Описание места учебного предмета в учебном плане
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения математики на этапе среднего (полного) общего образования отводится не менее 280 часов из расчета 4 часа в неделю.
Данная рабочая программа рассчитана на 85 часов (2.5 часа в неделю) , из них часов отводится на контрольные работы.
Содержание учебного предмета.
Тригонометрические функции ( 16 часов)
Обязательный минимум содержания образовательной области математика: область определения тригонометрических функций, множество значений тригонометрических функций, четность, нечетность, периодичность тригонометрических функций, свойства функций у=cosx, y=sinx, графики функций у=cosx, y=sinx, свойства функции y=tgx, график функции y=tgx
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Научиться находить область определения тригонометрических функций.
Научиться находить множество значений тригонометрических функций.
Научиться определять четность, нечетность, периодичность тригонометрических функций.
Знать свойства тригонометрических функций 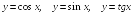 и уметь строить их графики.
и уметь строить их графики.
Уровень возможной подготовки обучающегося
Научиться находить область определения и множество значений тригонометрических функций в более сложных случаях.
Научиться определять четность, нечетность, периодичность тригонометрических функций в более сложных случаях.
Знать свойства тригонометрических функций 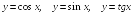 и уметь строить их графики. Уметь выполнять преобразования графиков.
и уметь строить их графики. Уметь выполнять преобразования графиков.
Описывать по графику и в простейших случаях по формуле поведение и свойства тригонометрических функций, находить по графику функции наибольшие и наименьшие значения;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для; практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Научится определять свойства обратных тригонометрических функций и выполнять эскизы их графиков, используя эти свойства.
Производная и ее геометрический смысл (16 часов)
Обязательный минимум содержания образовательной области математика: понятие о пределе и непрерывности функции, определение производной, правила дифференцирования, производная степенной функции, производные элементарных функций, геометрический смысл производной.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Понимать механический смысл производной.
Находить производные элементарных функций, пользуясь таблицей производных.
Находить производные элементарных функций, пользуясь правилами дифференцирования.
Понимать геометрический смысл производной.
Применение производной к исследованию функций ( 11 часов)
Обязательный минимум содержания образовательной области математика: возрастание и убывание функции, экстремумы функции, наибольшее и наименьшее значения функции, производная второго порядка, выпуклость и точки перегиба, построение графиков функции.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Применять производные для исследования функций на монотонность в несложных случаях.
Применять производные для исследования функций на экстремумы в несложных случаях.
Применять производные для исследования функций и построения их графиков в несложных случаях.
- Применять производные для нахождения наибольших и наименьших значений функции
Уровень возможной подготовки обучающегося
Научиться применять дифференциальное исчисление для исследования элементарных и сложных функций и построения их графиков.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Первообразная и интеграл (8 часов)
Обязательный минимум содержания образовательной области математика: первообразная, правила нахождения первообразных, площадь криволинейной трапеции, интеграл и его вычисление, вычисление площадей фигур с помощью интегралов для решения физических задач.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Научиться находить первообразные, пользуясь таблицей первообразных.
Научиться вычислять интегралы в простых случаях.
Научиться находить площадь криволинейной трапеции.
Уровень возможной подготовки обучающегося
Освоить технику нахождения первообразных.
Усвоить геометрический смысл интеграла.
Освоить технику вычисления интегралов.
Научиться находить площади фигур в более сложных случаях.
Комбинаторика (4 часа)
Обязательный минимум содержания образовательной области математика: правило произведения, размещения с повторениями, перестановки, размещения без повторений, сочетания без повторений и бином Ньютона
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь решать комбинаторные задачи.
Уровень возможной подготовки обучающегося
Элементы теории вероятностей (4 часа)
Обязательный минимум содержания образовательной области математика: вероятность события, сложение вероятностей, вероятность произведения независимых событий.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уровень возможной подготовки обучающегося
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией.
Уравнение и неравенство с двумя переменными (7 часов)
Обязательный минимум содержания образовательной области математика: линейные уравнения и неравенства с двумя переменными, нелинейные уравнения и неравенства с двумя переменными.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
применять методы решения уравнения с двумя переменными;
изображать множество точек, являющихся решением уравнения первой степени с двумя неизвестными;
решать неравенства с двумя переменными и их системы с помощью графиков;
Уровень возможной подготовки обучающегося
решать уравнения, простейшие системы уравнений с двумя неизвестными, используя свойства функций и их графиков;
решать уравнения, простейшие системы неравенств, используя свойства функций и их графиков; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
построения и исследования простейших математических моделей.
Итоговое повторение курса алгебры и начал анализа (19 часов)
Обязательный минимум содержания образовательной области математика
Корень степени n.
Степень с рациональным показателем.
Логарифм.
Синус, косинус, тангенс, котангенс. Прогрессии.
Общие приемы решения уравнений. Решение уравнений. Системы уравнений с двумя переменными. Неравенства с одной переменной.
Область определения функции.
Область значений функции.
Периодичность. Четность (нечетность). Возрастание (убывание).
Экстремумы. Наибольшее (наименьшее) значение.
Графики функций.
Производная.
Исследование функции с помощью производной.
Первообразная. Интеграл.
Площадь криволинейной трапеции.
Тематическое планирование
| № п/п | Наименование разделов и тем | Максимальная нагрузка учащегося, ч. | Из них |
|
| Теория ч. | Практическая часть |
|
| Конт..раб.
| Самост.работы | Тесты | ИКТ |
| I. | Тригонометрические функции | 16 | 7 | 1 | 3 | 2 | 9 |
| II. | Производная и ее геометрический смысл | 16 | 9 | 1 | 2 | 1 | 2 |
| III. | Применение производной к исследованию функции | 11 | 5 | 1 | 3 | 1 | 5 |
| IV | Первообразная и интеграл | 8 | 4 | 1 | 3 | 1 | 1 |
| V. | Комбинаторика | 4 | 4 | - | - | - | - |
| VI. | Элементы теории вероятностей | 4 | 3 | 1 | - | - | - |
| VII | Уравнения и неравенства с двумя переменными | 7 | 2 | 1 | 2 | - | 1 |
| VIII | Итоговое повторение курса алгебры и начал математического анализа | 19 | 13 | 1 | 3 | 3 | 10 |
|
| Итого | 85 | 47 | 7 | 16 | 7 | 28 |
Календарно -тематическое планирование
| № п/п | Наименование разделов и тем | Количество часов | Из них |
| Планир.дата | Фактич.дата |
| Теория ч. | Практическая часть |
|
| Контр.раб. | Самост. работы | Тесты | ИКТ |
| I | Тригонометрические функции | 16 |
|
|
|
|
|
|
|
| 1 | Область определения и множество значений тригонометрических функций |
| + |
|
|
| + |
|
|
| 2 | Область определения и множество значений тригонометрических функций |
|
|
| + |
|
|
|
|
| 3 | Четность, нечетность, переодичность тригонометрических функций |
| + |
|
|
|
|
|
|
| 4 | Четность, нечетность, переодичность тригонометрических функций |
|
|
|
| + | + |
|
|
| 5 | Переодичность тригонометрических функций |
| + |
|
|
| + |
|
|
| 6 | Свойства функции y=cos x и ее график |
| + |
|
|
| + |
|
|
| 7 | Свойства функции y=cos x и ее график |
|
|
|
|
|
|
|
|
| 8 | Свойства функции y=cos x и ее график |
|
|
|
|
|
|
|
|
| 9 | Свойства функции y=sin x и ее график |
| + |
|
|
| + |
|
|
| 10 | Свойства функции y=sin x и ее график |
|
|
|
|
|
|
|
|
| 11 | Свойства функции y=sin x и ее график |
|
|
| + |
|
|
|
|
| 12 | Свойства функции y=tg x и ее график |
| + |
|
|
| + |
|
|
| 13 | Свойства функции y=tg x и ее график |
|
|
|
|
|
|
|
|
| 14 | Обратные тригонометрические функции |
|
|
|
|
|
|
|
|
| 15 | Урок обобщения и систематизации знаний по теме « Тригонометрические функции» |
|
|
| + |
| + |
|
|
| 16 | Контрольная работа №1по теме « Тригонометрические функции» |
|
| + |
|
| + |
|
|
| II | Производная и ее геометрический смысл | 16 |
|
|
|
|
|
|
|
| 17 | Предел последовательности |
| + |
|
|
| + |
|
|
| 18 | Непрерывность функции |
| + |
|
|
|
|
|
|
| 19 | Определение производной |
| + |
|
|
|
|
|
|
| 20 | Определение производной |
|
|
|
|
|
|
|
|
| 21 | Правила дифференцирования |
| + |
|
|
|
|
|
|
| 22 | Правила дифференцирования |
| + |
|
|
|
|
|
|
| 23 | Правила дифференцирования |
|
|
| + |
|
|
|
|
| 24 | Производная степенной функции |
| + |
|
|
|
|
|
|
| 25 | Производная степенной функции |
|
|
|
|
|
|
|
|
| 26 | Производные элементарных функций |
| + |
|
| + |
|
|
|
| 27 | Производные элементарных функций |
|
|
|
|
|
|
|
|
| 28 | Производные элементарных функций |
|
|
|
|
|
|
|
|
| 29 | Геометрический смысл производной |
|
|
|
|
|
|
|
|
| 30 | Геометрический смысл производной |
| + |
|
|
|
|
|
|
| 31 | Урок обобщения и систематизации знаний «Производная и ее геометрический смысл» |
|
|
|
|
|
|
|
|
| 32 | Контрольная работа №2 по теме «Производная и ее геометрический смысл» |
|
|
|
|
|
|
|
|
| III | Применение производной к исследованию функции | 11 |
|
|
|
|
|
|
|
| 33 | Возрастание и убывание функции |
| + |
|
|
| + |
|
|
| 34 | Возрастание и убывание функции |
|
|
| + |
|
|
|
|
| 35 | Экстремумы функции |
| + |
|
|
|
|
|
|
| 36 | Экстремумы функции |
|
|
|
|
| + |
|
|
| 37 | Наибольшее и наименьшее значения функции |
|
|
|
| + | + |
|
|
| 38 | Наибольшее и наименьшее значения функции |
|
|
| + |
| + |
|
|
| 39 | Производная второго порядка, выпуклость и точки перегиба |
| + |
|
|
|
|
|
|
| 40 | Построение графиков функции |
|
|
| + |
| + |
|
|
| 41 | Построение графиков функции |
|
|
|
|
|
|
|
|
| 42 | Урок обобщения и систематизации знаний по теме «Применение производной к исследованию функции» |
|
|
|
|
|
|
|
|
| 43 | Контрольная работа №3 по теме «Применение производной к исследованию функции» |
|
|
|
|
|
|
|
|
| IV | Первообразная и интеграл | 8 |
|
|
|
|
|
|
|
| 44 | Первообразная |
| + |
|
|
|
|
|
|
| 45 | Первообразная |
|
|
| + |
|
|
|
|
| 46 | Правила нахождения первообразных |
| + |
|
|
|
|
|
|
| 47 | Правила нахождения первообразных |
|
|
| + |
|
|
|
|
| 48 | Площадь криволинейной трапеции. Интеграл и его вычисление. |
| + |
|
|
|
|
|
|
| 49 | Площадь криволинейной трапеции. Интеграл и его вычисление. |
|
|
| + |
|
|
|
|
| 50 | Применение интегралов для решения физических задач |
| + |
|
|
|
|
|
|
| 51 | Контрольная работа №4 по теме «Первообразная и интеграл» |
|
| + |
|
|
|
|
|
| V | Комбинаторика | 4 |
|
|
|
|
|
|
|
| 52 | Правило произведения. Размещения с повторениями. |
| + |
|
|
|
|
|
|
| 53 | Перестановки |
| + |
|
|
|
|
|
|
| 54 | Размещения без повторений |
| + |
|
|
|
|
|
|
| 55 | Сочетания без повторений и бином Ньютона |
| + |
|
|
|
|
|
|
| VI | Элементы теории вероятностей | 4 |
|
|
|
|
|
|
|
| 56 | Вероятность события |
| + |
|
|
|
|
|
|
| 57 | Сложение вероятностей |
| + |
|
|
|
|
|
|
| 58 | Вероятность произведения независимых событий |
| + |
|
|
|
|
|
|
| 59 | Контрольная работа по теме «Элементы теории вероятностей» |
|
| + |
|
|
|
|
|
| VII | Уравнения и неравенства с двумя переменными | 7 |
|
|
|
|
|
|
|
| 62 | Линейные уравнения и неравенства с двумя переменными |
| + |
|
|
|
|
|
|
| 63 | Линейные уравнения и неравенства с двумя переменными |
|
|
| + |
|
|
|
|
| 64 | Нелинейные уравнения и неравенства с двумя переменными |
| + |
|
|
|
|
|
|
| 65 | Нелинейные уравнения и неравенства с двумя переменными |
|
|
| + |
|
|
|
|
| 66 | Контрольная работа №6 по теме «Уравнения и неравенства с двумя переменными» |
|
| + |
|
|
|
|
|
| VIII | Итоговое повторение курса алгебры и начал математического анализа | 19 |
|
|
|
|
|
|
|
| 67 | Репетиционный экзамен в формате ЕГЭ (2016) |
|
| + |
|
|
|
|
|
| 68 | Репетиционный экзамен в формате ЕГЭ (2016) |
|
| + |
|
|
|
|
|
| 69 | Репетиционный экзамен в формате ЕГЭ (2016) |
|
| + |
|
|
|
|
|
| 70 | Репетиционный экзамен в формате ЕГЭ (2016) |
|
| + |
|
|
|
|
|
| 71 | Повторение главы IV (10 класс), Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 72 | Повторение главы V (10 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 73 | Повторение главы VI (10 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 74 | Повторение главы VII (10 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 75 | Повторение главы VIII (10 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 76 | Повторение главы IX (10 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 77 | Повторение главы I (11 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 78 | Повторение главы II (11 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 79 | Повторение главы III (11 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 80 | Повторение главы IV (11 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 81 | Повторение главы V (11 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 82 | Повторение главы VI (11 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 83 | Повторение главы VII (11 класс) Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
| 84 | Итоговая контрольная работа |
|
|
|
|
|
|
|
|
| 85 | Анализ контрольной работы. Решение задач из КИМ ЕГЭ |
|
|
|
|
|
|
|
|
|
| Итого | 85 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Планируемые результаты изучения учебного предмета
на базовом уровне.
В результате изучения математики на базовом уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира;
Алгебра
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Начала математического анализа
уметь
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера;
Учебно-методическое обеспечение предмета
Для учителя:
1.Программа для общеобразовательных учреждений по алгебре для 10-11 классов, составительБурмистрова Т.А., автор Колягин Ю.М. – М.: Просвещение, 2011г.
2. Учебник: Алгебра и начала анализа для 11 класса, авторов: Ю.М.Колягин, Ю.В.Сидоров, М.В.Ткачёва, Н. Е.Фёдорова и М.И.Шабунин, под редакцией А.Б.Жижченко, – М.: Просвещение, 2011г.
3. Дидактические материалы для 11 класса «Алгебра и начала математического анализа» авторов: М.И.Шабунин, М.В.Ткачёва,
Н.Е.Фёдорова, О. Н. Доброва, – М.: Просвещение, 2012г.
4.Единый государственный экзамен 2010-2013 г.. Математика. Учебно-тренировочные материалы для подготовки учащихся / ФИПИ-М.: Интеллект-Центр, 2010-2013.
Для учащихся:
1. Учебник: Алгебра и начала анализа для 11 класса, авторов: Ю.М.Колягин, Ю.В.Сидоров, М.В.Ткачёва, Н. Е.Фёдорова и М.И.Шабунин, под редакцией А.Б.Жижченко, – М.: Просвещение, 2011г.
2. Дидактические материалы для 11 класса «Алгебра и начала математического анализа» авторов: М.И.Шабунин, М.В.Ткачёва,
Н.Е.Фёдорова, О. Н. Доброва, – М.: Просвещение, 2012г.
Дополнительная литература:
1. Федеральный перечень учебников, рекомендуемых Министерством образования РФ к использованию в общеобразовательном процессе в общеобразовательных учреждениях на 2013-2014 учебный год.
2. Математика. Еженедельное приложение к газете «Первое сентября».
3. Математика в школе. Еженедельный научно-методический журнал.
Интернет-ресурсы:
1. Министерство образование РФ: http//www.ed.ru/ http//www.edu.ru
2. Тестирование online: 5-11 классы: http//www.kokch.kts.ru/cdo
3. Досье школьного учителя математики: http//www.mathvaz.ru
4. Новые технологии в образование: http//www.edu.secna.ru
5. Мегаэнциклопедия Кирилла и Мефодия: http//www.mega.km.ru
6. Сайты «Энциклопедий»: http//www.rubricon.ruhttp//www.encyclopedia.ru
7. Сайт для самообразования и он-лайн тестирования: http//www.bztest.ru
8.Сайт федеральных педагогических измерений: www.fipi.ru
Список источников к программе
1. Федеральный Закон «Об образовании в Российской Федерации».
2. Федеральные государственные образовательные стандарты общего образования (ФГОС ОО).
3. Концепция духовно-нравственного развития и воспитания личности гражданина России в сфере общего образования.
4. Приказ Министерства труда и социальной защиты Российской Федерации от 18 октября 2013 г. № 544-н «Об утверждении профессионального стандарта «Педагог (педагогическая деятельность в сфере дошкольного, начального общего, основного общего, среднего общего образования) (воспитатель, учитель)».
5. Федеральный компонент государственного образовательного стандарта (ФК ГОС).
6. Примерные программы основного общего и среднего (полного) общего образования по математике (письмо Департамента государственной политики в образовании Министерства образования и науки Российской Федерации).
7. Приказ Министерства образования и науки «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2014 – 2017 учебный год».
8. Закон Республики Мордовия «Об образовании в Республике Мордовия».
9. Распоряжение правительства Российской Федерации «О Концепции развития математического образования в Российской Федерации».
10. Методические рекомендации по реализации Концепции математического образования в Республике Мордовия на 2014 – 2020 гг.
11. Федеральный перечень учебников на 2014 - 2015уч. год утвержден приказом Минобрнауки РФ от 31 марта 2014 г. № 253;
12. Федеральная служба по надзору в свете защиты прав потребителей и благополучия человека. Постановление Главного государственного санитарного врача РФ от 29 декабря 2010 г. № 189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях»», с изменениями.
5







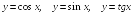 и уметь строить их графики.
и уметь строить их графики.


















