Рабочая программа по алгебре 9 класс

Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования.

Интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей.

Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.

Воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Знать/понимать

Уметь

9 класс

- значение математической науки для решения задач, возникающих в теории и практике;

- широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

- значение практики и вопросов, возникающих в самой математике, для формирования и развитие математической науки;

- историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;

- универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;

- вероятностный характер различных процессов окружающего мира.

- выполнять арифметические действия, сочетая устные и письменные приемы; находить значение корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;

- составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

- выполнять основные действия со степенями с цельными показателями, с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

- применять свойства арифметических квадратов корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

- решать линейные, квадратные уравнения, рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные уравнения;

- решать линейные и квадратные неравенства с одной переменной и их системы;

- решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

- изображать числа точками на координатной прямой;

- определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;

- распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;

- находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;

- определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;

- описывать свойства изученных функций, строить их графики;

- извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

- вычислять средние значения результатов измерений;

- находить частоту события, используя собственные наблюдения и готовые статистические данные;

- находить вероятности случайных событий в простейших случаях.

7 класс

8 класс

9 класс

Арифметика

Натуральные числа

Степень с натуральным показателем

Дроби

Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной.

Рациональные числа

Этапы развития представления о числе

Запись больших и маленьких чисел с использованием степеней числа 10

Действительные числа

Упорядочение знаний о классах действительных чисел.

Бесконечные десятичные дроби.

Сравнение действительных чисел, арифметические действия над ними, соотнесение их с координатной прямой.

Числовые последовательности

Понятие последовательности.

Арифметическая и геометрическая прогрессии.

Формулы общего члена арифметической и геометрической прогрессий, суммы первых нескольких членов арифметической и геометрической прогрессий.

Сложные проценты.

Измерения, приближения, оценки

Размеры объектов окружающего мира (от элементарных частиц до Вселенной).

Представление зависимости между величинами в виде формул

Проценты. Нахождение процента от величины, величины по ее проценту.

Алгебра

Алгебраические выражения

Буквенные выражения. Числовое значение буквенного выражения. Равенство буквенных выражений.

Рациональные выражения и их преобразования

Преобразование буквенных выражений: раскрытие скобок, приведение подобных слагаемых.

Свойства степеней с натуральными показателями

Многочлены

Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности. Формула разности квадратов, формула суммы кубов и разности кубов. Разложение многочлена на множители.

Уравнения и неравенства

Уравнение с одной переменной

Решение рациональных уравнений второй степени.

Решение рациональных уравнений. Примеры решения уравнений высших степеней; метод замены переменной, разложения на множители.

Корень уравнения

Уравнение с двумя переменными; решение уравнения с двумя переменными. Уравнение с несколькими переменными. Примеры решения нелинейных систем. Примеры решения уравнений в целых числах.

Линейное уравнение

Неравенство с одной переменной. Решение неравенств. Линейные неравенства с одной переменной и их системы. Квадратные неравенства. Примеры решения дробно- линейных неравенств.

Переход от словесной формулировки соотношений между величинами к алгебраической

Числовые неравенства и их свойства. Доказательство числовых и алгебраических неравенств

Решение текстовых задач алгебраическим способом

Координаты

Числовые промежутки: интервал, отрезок, луч

Формула расстояния между двумя точками плоскости

Декартовы координаты на плоскости

Графическая интерпретация уравнений с двумя переменными и их систем, неравенств с двумя переменными и их систем.

Координаты середины отрезка

Уравнение прямой

Числовые функции

Чтение графиков функций

Графическая интерпретация уравнений с двумя переменными и их систем.

Квадратичная функция, ее график, парабола. Возрастание и убывание квадратичной функции, ее наибольшее и наименьшее значение, нули, промежутки знакопостоянства. Координаты вершины параболы, ось симметрии.

Графики реальных зависимостей

Степенные функции с натуральным показателем, их графики

Использование графиков для решения уравнений и систем

Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост. Числовые функции, описывающие эти процессы.

Параллельный перенос графиков вдоль осей координат и симметрия относительно осей

Элементы логики, комбинаторики, статистики и теории вероятностей

Доказательство.

Определения, доказательства, следствия. Контрпример.

Множества и комбинаторика

Множество. Элемент множества, подмножество. Объединение и пересечение множеств. Диаграммы Эйлера.

Примеры решения комбинаторных задач: правило умножения, формула для вычисления числа перестановок.

Статистические данные

Представление данных в виде таблиц, диаграмм, графиков

Понятие о статистическом выводе на основе выборки

Средние результатов измерений.

Понятие и примеры случайных событий

Понятие о статистическом выводе

Вероятность

Частота события, вероятность

Равновозможные события и подсчет их вероятности

Классическая формула подсчета вероятностей

Геометрические вероятности

Линейные и квадратные неравенства (повторение).

Рациональное неравенство. Метод интервалов.

Множества и операции над ними.

Система неравенств. Решение системы неравенств.

Рациональное уравнение с двумя переменными. Решение уравнения p(x,y)=0. Формула расстояния между двумя точками координатной плоскости. График уравнения (x - a)²+(y - b)²=r². Система уравнений с двумя переменными. Решение системы уравнений. Неравенства и системы неравенств с двумя переменными.

Методы решения систем уравнений (метод подстановки, алгебраического сложения, введения новых переменных).

Системы уравнений как математические модели реальных ситуаций.

Функция. Независимая переменная. Зависимая переменная. Область определения функции. Естественная область определения функции. Область значений функции.

Способы задания функции (аналитический, графический, табличный, словесный).

Свойства функций (монотонность, ограниченность, выпуклость, наибольшее и наименьшее значения, непрерывность). Исследование функций: y= C, y=kx+m, y=kx², y=k/x, y=ax²+bx+c, y=, y=|x|.

Четные и нечетные функции. Алгоритм исследования функции на четность. Графики четной и нечетной функций.

Степенная функция с натуральным показателем, ее свойства и график. Степенная функция с отрицательным целым показателем, ее свойства и график.

Функция , ее свойства и график.

Числовая последовательность. Способы задания числовых последовательностей (аналитический, словесный, рекуррентный). Свойства числовых последовательностей.

Арифметическая прогрессия. Формула n-го члена. Формула суммы членов конечной арифметической прогрессии. Характеристическое свойство.

Геометрическая прогрессия. Формула n-го члена. Формула суммы членов конечной геометрической прогрессии. Характеристическое свойство. Прогрессии и банковские расчеты.

Комбинаторные задачи. Правило умножения. Факториал. Перестановки.

Группировка информации. Общий ряд данных. Кратность варианты измерения. Табличное представление информации. Частота варианты. Графическое представление информации. Полигон распределения данных. Гистограмма. Числовые характеристики данных измерения (размах, мода, среднее значение).

Вероятность. Событие (случайное, достоверное, невозможное). Классическая вероятностная схема. Противоположные события. Несовместные события. Вероятность суммы двух событий. Вероятность противоположного события. Статистическая устойчивость. Статистическая вероятность.

№

Тема

Количество часов

Контрольные и диагностические материалы

1

Вводное повторение

4

2

Неравенства и системы неравенств

15

1

3

Системы уравнений

15

1

4

Числовые функции

24

2

5

Прогрессии.

16

1

6

Элементы комбинаторики, статистики и теории вероятностей

12

1

7

Повторение.

16

1

Всего

102

7

№ урока

Дата проведения (по плану)

Дата проведения (фактическая)

Наименование разделов и тем уроков

Кол-во

часов

Домашнее задание

Тип урока

Элементы содержания образования

Основные виды деятельности

Вводное повторение

1

1.09

Действия над многочленами. Формулы сокращенного умножения. Основные методы разложения на множители.

1

№1, 3 стр.5

Комбинированный

2

4.09

Преобразование числовых и алгебраических выражений. Решение уравнений.

1

№21, 28 стр. 7-9

Применение и совершенствование знаний

3

5.09

Функция. Виды функций. Построение графиков функций

1

№7г, 11г, 13б стр. 6

Комбинированный

4

8.09

Математические модели реальных ситуаций.

1

Применение и совершенствование знаний

Глава 1

Неравенства и системы неравенств

15

§ 1.

Линейные и квадратные неравенства

3

Иметь представление о решении линейных и квадратных неравенств с одной переменной.

Знать, как проводить исследование функции на монотонность.

Уметь:

– решать линейные и квадратные неравенства с одной переменной, содержащие модуль;

– решать неравенства, используя графики.

.

5

11.09

Неравенство с одной переменной. Линейные неравенства. Решение неравенства.

1

П. 1 стр. 5 – 13;

№1.1а, б 1.3а, б, 1.4, а, б стр. 11

Комбинированный

6

12.09

Квадратные неравенства. Решение неравенства.

1

№1.8, 1.12 стр. 12

Комбинированный

7

15.09

Линейные и квадратные неравенства. Равносильные неравенства.

1

№1.16, а, б, 1.17 стр. 13

Комплексное применение знаний и умений

§ 2.

Рациональные неравенства

5

Иметь представление о решении рациональных неравенств методом интервалов.

Знать и применять правила равносильного преобразования неравенств

Уметь:

-решать дробно-рациональные неравенства методом интервалов, в случае различных кратностей корней линейных выражений,

-применяют правила равносильного преобразования неравенств.

8

18.09

Рациональные неравенства с одной переменной.

1

П.2 стр. 13 – 25; №2.2, 2.3 стр. 14

Усвоение новых знаний

9

19.09

Рациональные неравенства.

1

№2.6, 2.7, а, б стр. 14

Комбинированный

10

22.09

Решение рациональных неравенств.

1

№2.9, 2.16, а, б стр. 15

Комбинированный

11

25.09

Решение рациональных неравенств методом интервалов.

1

№2.13, 2.15, а, б стр. 15

Применение и совершенствование знаний

12

26.09

Рациональные неравенства. Решение неравенств.

1

№2.20а, б, 2.21 стр. 16

Комплексное применение знаний и умений

§ 3.

Множества и операции над ними

2

Элемент множества, подмножество данного множества, пустое множество. Пересечение и объединение множеств

Знать определение простейшие понятия теории множеств.

Уметь задавать множества, производить операции над множествами

Уметь решать текстовые задачи, используя круги Эйлера.

13

29.09

Понятие множества. Подмножества.

1

П. 3 стр. 25 – 32; №3.4, 3.6, а, б, 3.16 стр. 20 - 21

Усвоение новых знаний

14

02.10

Операции над множествами: пересечение, объединение.

1

П.3 стр. 32 – 42; № №3.7, 3.12, а, б стр. 20

Комбинированный

§ 4.

Системы рациональных неравенств

4

Системы линейных неравенств, частное и общее решение системы неравенств

Знать способы решения систем рациональных неравенств.

Уметь:

- решать системы линейных и квадратных неравенств,

-решать двойные неравенства,

-решать системы простых рациональных неравенств методом интервалов,

– решать системы квадратных неравенств, используя графический метод.

15

03.10

Системы рациональных неравенств. Двойные неравенства.

1

П. 4 стр. 42 – 50; №4.3, 4.5 стр. 23

Усвоение новых знаний

16

06.10

Решение систем рациональных неравенств.

1

№4.9, 4.11 стр. 24

Комбинированный

17

09.10

Математическая модель реальной ситуации. Решение текстовых задач алгебраическим способом.

1

№4.13, 4.15 стр. 25

Применение и совершенствование знаний

18

10.10

Обобщение знаний по теме «Неравенства и системы неравенств»

1

Стр. 29 – 30 №3, 5, 6, 8

Систематизация и обобщение знаний и умений

19

13.10

Контрольная работа №1 по теме «Неравенства и системы неравенств»

1

Контроль знаний и умений

Глава 2

Системы уравнений

15

Рациональное уравнение с двумя переменными, решение уравнения с двумя переменными, равносильные уравнения, равносильные преобразования, график уравнения, система уравнений, решение системы уравнений.

Иметь понятие о решении системы уравнений и неравенств.

Знать равносильные преобразования уравнений и неравенств с двумя переменными.

Уметь определять понятия, приводить доказательства.

§ 5.

Основные понятия

3

20

16.10

Рациональные уравнения с двумя переменными. Решение рациональных уравнений. График уравнения с двумя переменными.

1

П. 5 стр. 52 – 60; №5.1, 5.2, 5.4 а. Б стр. 32

Усвоение новых знаний

21

17.10

Формула расстояния между точками координатной плоскости. График уравнения (х – a)²+(y- b)² = r²

1

П. 5 стр. 60 – 63; №5.3, а, б, 5.8, а, 5.15а стр. 32 - 35

Комбинированный

22

20.10

Системы уравнений с двумя переменными. Использование графика функции при решении систем уравнений и систем неравенств.

1

П. 5 стр. 64 – 70; №5.18, а, б, 5.21а, 5.22а, б, 5.25, а, б стр. 36 - 37

Применение и совершенствование знаний

§ 6.

Методы решения систем уравнений

5

Знать: метод подстановки, метод алгебраического сложения, метод замены переменной (введения новых переменных), равносильные системы уравнений. Алгоритм метода подстановки.

Уметь решать системы уравнений методом подстановки, методом алгебраического сложения, методом замены переменной (введения новых переменных).

23

23.10

Система уравнений; решение системы методом подстановки.

1

П. 6 стр. 72 – 73; № №6.2, 6.4, а, б стр. 39

Комбинированный

24

24.10

Система уравнений; решение системы методом алгебраического сложения.

1

П. 6 стр. 73 – 74; №6.6, 6.8, а, б стр. 40

Комбинированный

25

06.11

Решение систем уравнений методом подстановки и методом алгебраического сложения.

1

П. 6 стр. 72 – 74; №6.5а, б, 6.4 виг стр. 39 - 40

Применение и совершенствование знаний

26

07.11

Система уравнений; решение системы методом замены переменной.

1

П.6 стр. 75 – 78; №6.9 стр. 40

Комбинированный

27

10.11

Решение систем уравнений, используя разные методы.

1

№6.16а, б, 6.14 стр. 41

Комплексное применение знаний и умений

§ 7.

Системы уравнений как математические модели реальных ситуаций

6

Составление математической модели, работа с составленной моделью, система двух нелинейных уравнений, применение всех методов решение системы уравнении

Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью.

Уметь составлять математические модели реальных ситуаций и работать с составленной моделью.

Уметь решать простые нелинейные системы уравнений двух переменных различными методами, составлять математические модели реальных ситуаций и работать с составленной моделью.

28

13.11

Системы уравнений как математические модели реальных ситуаций.

1

П. 7 стр. 79 – 86; № 7.3, 7.4 стр. 44

Усвоение новых знаний

29

14.11

Три этапа математической модели.

1

№7.11, 7.12 стр. 45

Комбинированный

30

17.11

Составление математической модели при решении задач.

1

№7.17, 7.18 стр. 45

Комбинированный

31

20.11

Решение текстовых задач с помощью систем уравнений.

1

№7.23, 7.24 стр. 46

Комплексное применение знаний и умений

32

21.11

Составление математических моделей при решении текстовых задач алгебраическим способом.

1

№7.27, 7.28 стр. 47

Комплексное применение знаний и умений

33

24.11

Обобщение знаний по теме «Системы уравнений»

1

Стр. 52 №4, 5, 6, 9

Систематизация и обобщение знаний и умений

34

27.11

Контрольная работа №2 на тему «Системы уравнений»

1

Контроль знаний и умений

Глава 3

Числовые функции

24

§ 8.

Определение числовой функции. Область определения, область значения функции

4

Функция, независимая и зависимая переменная, область определение и множество значений функции, график функции, кусочно-заданная функция

Знать определения числовой функции, области определения, области значения функции, графика функции.

Уметь находить область определения функции.

35

28.11

Определение числовой функции.

1

П. 8 стр. 88 – 96; №8.2, 8.3 стр. 55

Усвоение новых знаний

36

01.12

Понятие функции. Область определения функции.

1

№8.6, 8.8а, б, 8.9 стр. 56

Комбинированный

37

4.12

График функции. Область значения функции.

1

№8.14, 8.16а, б, 8.18а, б стр. 57

Комбинированный

38

05.12

Нахождение области определения функции.

1

№8.22, 8.27 стр. 57 - 59

Комбинированный

§ 9.

Способы задания функций

2

Способы задания функции (аналитический, графический, табличный, словесный).

Знать способы задания функции: аналитический, графический, табличный, словесный.

Уметь:

-при задании функции применять различные способы: аналитический, графический, табличный, словесный,

- решать графически уравнения.

39

08.12

Способы задания функции.

1

П. 9 стр. 96 – 102; №9.2, 9.4 стр. 61 – 62

Комбинированный

40

11.12

Аналитический, графический, табличный и словесный способы задания функции.

1

№9.7, 9.9б, г стр. 65

Комплексное применение знаний и умений

§ 10.

Свойства функций

4

Возрастающая и убывающая на множестве функция, монотонная функция, исследование на монотонность, ограниченная снизу, ограниченная сверху на множестве функции, ограниченная функция, наименьшее и наибольшее значения на множестве, непрерывная функция, выпуклая вверх, выпуклая вниз, элементарные функции.

Знать свойства функции: монотонность, наибольшее и наименьшее значения функции, ограниченность, выпуклость и непрерывность.

Уметь исследовать функции на монотонность, наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность.

41

12.12

График функции, возрастание и убывание функции. Монотонность функции.

1

П.10 стр. 103 – 115; 10.2, 10.7 стр. 68 - 69

Комбинированный

42

15.12

Наибольшее и наименьшее значения функции.

1

№10.11а, б, 10.13а, б, 10.15 стр. 69

Комбинированный

43

18.12

Ограниченность, выпуклость и непрерывность функции.

1

№10.9, 10.14астр.69

Комбинированный

44

19.12

Нули функции, промежутки знакопостоянства.

1

Комбинированный

§ 11.

Чётные и нечётные функции

3

Четная функция, нечетная функция, симметричное множество, алгоритм исследования функции на четность, график нечетной функции, график четной функции.

Знать понятия четной и нечетной функции, алгоритм исследования функции на чётность и нечётность.

Уметь применять алгоритм исследования функции на четность и строить графики четных и нечетных функций

45

22.12

Чётные и нечётные функции

1

П. 11 стр. 116 – 122; №11.3а, б, 11.4а, б, 11.6а, б стр. 72

Усвоение новых знаний

46

25.12

Алгоритм исследования функции на четность. Симметричность множества.

1

№ 11.8а, б, 11.10, 11.15, 11.17 стр. 75

Комбинированный

47

26.12

Обобщение знаний по теме «Числовые функции»

1

Стр. 89 №1, 4, 10

Систематизация и обобщение знаний и умений

48

29.12

Контрольная работа №3 по теме «Определение числовой функции. Свойства числовой функции»

1

Контроль знаний и умений

§ 12.

Функция у = хⁿ (nN), их свойства и графики

3

Степенная функция с натуральным показателем, свойства и график степенной функции с натуральным показателем, свойства и график степенной функции с четным показателем, свойства и график степенная функция с нечетным показателем, решение уравнений графически

Знать о понятии степенной функции с натуральным показателем, о свойствах и графике функции.

Уметь:

- определять графики функций с четным и нечетным показателем,

-строить и читать графики степенных функций.

49

09.01

Степенные функции с натуральным показателем.

1

П. 12 стр. 122 – 129; № 12.4, 12.6а, 12.7а, б стр. 78

Усвоение новых знаний

50

12.01

Свойства степенных функций с натуральным показателем.

1

№12.11, 12.13а, б стр. 79

Комбинированный

51

15.01

Графики степенных функций с натуральным показателем.

1

№12.18а, 12.17а, б, 12.19, а стр. 79 - 80

Комплексное применение знаний и умений

§ 13.

Функция у = х^-n (nN), их свойства и графики

3

Степенная функция с отрицательным целым показателем, её свойства и график, график степенная функция с четным отрицательным целым показателем, график степенная функция с нечетным отрицательным целым показателем, решение уравнений графически.

Знать о понятии степенной функции с отрицательным целым показателем, о свойствах и графике функции.

Уметь:

- определять графики функций с четным и нечетным отрицательным целым показателем,

-решать графически уравнения,

-строить графики степенных функций с любым показателем

52

16.01

Степенные функции с отрицательным показателем.

1

П. 13 стр. 130 – 137; №13.3а, б, 13.6 стр. 83

Усвоение новых знаний

53

19.01

Свойства степенных функций с отрицательным показателем.

1

№13.8, 13.9а, б, 13.10а стр. 83

Комбинированный

54

22.01

Графики степенных функций с отрицательным показателем.

1

№13.11а, 13.12стр. 84

Комплексное применение знаний и умений

§ 14.

Функция у=³√х , её свойства и график

3

Функция кубического корня, график функции у=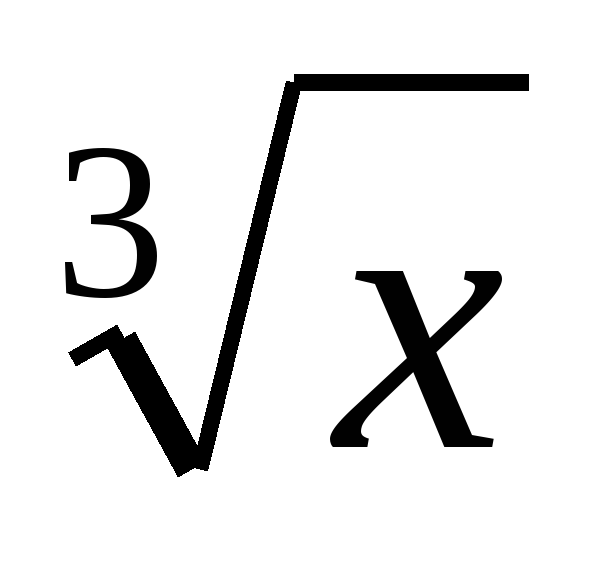,свойства данной функции.

Знать определение функции кубического корня, её свойства. Уметь:

– определять график функции кубического корня,

– строить график функции кубического корня,

– читать свойства по графику функции.

55

23.01

Функция корень кубический.

1

П. 14 стр. 137 – 144; №14.2, 14.3, 14.9 стр. 86

Комбинированный

56

26.01

Свойства и график функции корень кубический.

1

№14.15а, б, 14.17 стр. 87

Комплексное применение знаний и умений

57

29.01

Обобщение знаний по теме «Степенная функция».

1

Стр. 89 №6, 7, 10

Систематизация и обобщение знаний и умений

58

30.01

Контрольная работа №4 по теме «Степенные функции, их свойства и графики»

1

Контроль знаний и умений

Глава 4

Прогрессии

16

§ 15.

Числовые последовательности

4

Числовая последовательность, способы задания последовательности (аналитическое, словесное, рекуррентное), свойства числовых последовательностей, монотонные последовательности (возрастающая, убывающая).

Знать определение числовой последовательности, способы задания числовой последовательности.

Уметь задать числовую последовательность аналитически, словесно, рекуррентно.

59

02.02

Понятие последовательности. Числовые последовательности.

1

П. 15 стр. 146 – 149; №15. 2а, б, 15.4 15.8 стр. 91 - 92

Усвоение новых знаний

60

05.02

Аналитическое задание последовательности

1

П.15 стр. 149 – 152; №15.12, 15.15, а, б стр. 92

Комбинированный

61

06.02

Словесное и рекуррентное задание последовательности

1

П.15стр. 152 – 154; №15.18, 15.20а, б стр. 93

Комбинированный

62

09.02

Монотонные последовательности

1

П. 15 стр. 154 – 155; №15.22а, б, 15.23а, б, 15.26а, б стр. 93

Комбинированный

§ 16.

Арифметическая прогрессия

4

Арифметическая прогрессия, разность, возрастающая прогрессия, конечная прогрессия, формула n-го члена арифметической прогрессии, формула суммы членов конечной арифметической прогрессии, характеристическое свойство арифметической прогрессии.

Знать определение и формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии, характеристическое свойство арифметической прогрессии.

Уметь:

-применять формулы n-го члена арифметической прогрессии, суммы членов конечной арифметической прогрессии при решении задач,

- применять характеристическое свойство арифметической прогрессии при решении математических задач.

63

12.02

Арифметическая прогрессия. Разность прогрессии.

1

П. 16 стр. 156 – 157; №16.2, 16.4, 16.8 стр. 97

Усвоение новых знаний

64

13.02

Формула общего (n-го) члена арифметической прогрессии

1

П.16 стр. 157 – 161; №16.7а, б, 16.14, 16.18а, б стр. 98 - 99

Комбинированный

65

16.02

Сумма первых нескольких членов арифметической прогрессии

1

П.16 стр. 161 – 165; №16.25, 16.27 стр. 100

Комбинированный

66

19.02

Характеристическое свойство арифметической прогрессии

1

П. 16 стр. 165 – 166; №16.32, 16.34, 16. 38 стр. 101

Комплексное применение знаний и умений

§ 17.

Геометрическая прогрессия

7

Геометрическая прогрессия, знаменатель прогрессии, возрастающая прогрессия, конечная прогрессия, формула n-го члена геометрической прогрессии, показательная функция, формула суммы членов конечной геометрической прогрессии, характеристическое свойство геометрической прогрессии, формула простых и сложных процентов.

Знать определение и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии, характеристическое свойство геометрической прогрессии.

Уметь применять формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии, характеристическое свойство геометрической прогрессии при решении задач.

67

20.02

Геометрическая прогрессия. Знаменатель прогрессии.

1

П. 17 стр. 167 – 168; №17.1а, б, 17.3, 17.6, 17.8а, б стр. 107

Усвоение новых знаний

68

26.02

Формула общего (n-го) члена геометрической прогрессии

1

П.17 стр. 169 – 174; №17.13а, б, 17.14а, б, 17.16а, 17.18а, б стр. 108

Комбинированный

69

27.02

Сумма первых нескольких членов геометрической прогрессии

1

П.17 стр. 175 – 176; №17.25, 17.28 стр. 111

Комбинированный

70

02.03

Характеристическое свойство геометрической прогрессии

1

П. 17 стр. 177 – 180; №17.30, 17.31а, б стр. 111

Комплексное применение знаний и умений

71

05.03

Простые и сложные проценты.

1

П. 17 стр. 180 – 181; №17.35, 17.33 стр. 112

Усвоение новых знаний

72

06.03

Решение текстовых задач на использование простых и сложных процентов

1

Индивидуальные задания

Комплексное применение знаний и умений

73

09.03

Обобщение знаний по теме «Прогрессии»

Стр. 116 №7, 8, 9

Систематизация и обобщение знаний и умений

74

12.03

Контрольная работа №5 по теме «Прогрессии»

1

Контроль знаний и умений

Глава 5

Элементы комбинаторики, статистики и теории вероятностей

12

§ 18.

Комбинаторные задачи

3

Метод перебора вариантов, дерево возможных вариантов, правило умножения, факториал.

Знать, как решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения

Уметь решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения.

75

13.03

Комбинаторные задачи

1

П. 18 стр. 184 – 193; №18.3, 18.4 стр. 118

Усвоение новых знаний

76

16.03

Правило умножения. вычисление факториала

1

П. 18 стр. 188 – 190 №18.18.9, 18.12 стр. 120

Усвоение новых знаний

77

19.03

Примеры решения комбинаторных задач: перебор вариантов, правило умножения.

1

№18.16, 18.17 стр. 120

Комбинированный

§ 19.

Статистика: дизайн информации

3

Методы статистической обработки результатов измерений, общий ряд данных и ряд данных конкретного измерения, варианта ряда данных, её кратность, частота и процентная частота, сгруппированный ряд данных, многоугольники

распределения, числовые характеристики информации (мода, объем, размах, среднее).

78

20.03

Статистические данные. Представление данных в виде таблиц, диаграмм, графиков.

1

П. 19 стр. 194 – 203; №19.4 стр. 124

Усвоение новых знаний

79

02.04

Средние результатов измерений.

1

П.19 стр. 204 – 208; № 19.7 стр. 125

Комбинированный

80

03.04

Понятие о статистическом выводе на основе выборки. Понятие и примеры случайных событий.

1

№19.9 стр. 126

Комбинированный

§ 20.

Простейшие вероятностные задачи

3

Случайные события: достоверное и невозможное события, несовместные события, событие, противоположное данному событию, сумма двух случайных событий. Классическая вероятностная схема. Классическое определение вероятности

Знать классическую вероятностную схему, классическое определение вероятности, понятия случайное событие, достоверное и невозможное события, несовместные события, события, противоположные данному событию.

Уметь находить вероятность события.

81

06.04

Частота события, вероятность.

1

П.20 стр. 209 -213; № 20.4 стр.130

Усвоение новых знаний

82

09.04

Равновозможные события и подсчет их вероятности.

1

П.20 стр. 214 – 220; №20.8, 20.9 стр. 131

Комбинированный

83

10.04

Представление о геометрической вероятности.

1

П. 20 стр. 220 – 222; №20.12 стр. 131

Комбинированный

§ 21.

Экспериментальные данные и вероятности событий

2

Статистическая устойчивость, статистическая вероятность.

Иметь представление о статистической устойчивости, статистической вероятности.

Уметь решать простейшие статистические задачи

84

13.04

Экспериментальные данные и вероятности событий

1

П. 21 стр. 223 – 228; №21.3 стр.134

Комплексное применение знаний и умений

85

16.04

Статистическая устойчивость. Статистическая вероятность события.

1

Стр. 229 основные результаты, домашняя контрольная работа № 5 стр. 138

Систематизация и обобщение знаний и умений

86

17.04

Контрольная работа №6 по теме «Элементы комбинаторики, статистики и теории вероятностей»

1

Контроль знаний и умений

Итоговое повторение

16

87

20.04

Числовые выражения

1

Комплексное применение знаний и умений

88

23.04

Алгебраические выражения

1

89

24.04

Алгебраические выражения

1

90

27.04

Функции и графики

1

91

30.04

Функции и графики

1

92

04.05

Уравнения и системы уравнений

1

93

07.05

Уравнения и системы уравнений

1

94

08.05

Неравенства и системы неравенств

1

95

11.05

Неравенства и системы неравенств

1

96

14.05

Задачи на составление уравнений

1

97

15.05

Задачи на составление систем уравнений

1

98

18.05

Задачи на составление уравнений или систем уравнений

1

99

21.05

Арифметические и геометрические прогрессии

1

100

22.05

Итоговая контрольная работа

1

Контроль знаний и умений

101

25.05

Анализ итоговой контрольной работы

1

102

Подведение итогов.

1