Рабочая программа по геометрии для 9 класса

Рабочая программа по геометрии для 9 класса.

Составитель: Соловьева Н.Н., учитель математики

МБОУ «Средняя школа № 83» г.Ульяновска

Данная программа составлена на основе программы:Геометрия.

Сборник рабочих программ.7-9 классы.(Сост.Бурмистрова Т.А.).

Учебник:Геометрия.7-9 классы.(Атанасян Л.С.,Бутузов В.Ф., Кадомцев С.П.)

1.Планируемые результаты освоения учебного предмета.

ЛИЧНОСТНЫЕ

По окончании изучения курса выпускник научится:

• умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

• критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

• представление о математической науке как сфере человеческой деятельности, об этапах ее раз-вития, о ее значимости для развития цивилизации;

могут быть сформированы:

• креативность мышления, инициатива, находчивость, активность при решении математических задач;

• умение контролировать процесс и результат учебной математической деятельности;

• способность к эмоциональному восприятию математических объектов, задач, решений, рас-суждений.

ПРЕДМЕТНЫЕ

По окончании изучения курса выпускник научится:

• выполнять действия над векторами:сложение векторов,применяя правила треугольника,параллелограмма, многоугольника; вычитание векторов; умножения вектора на число;

• выражать векторы через два неколлинеарных вектора;

• вычислять координаты вектора по координатам его начала и конца;

• вычислять координаты середины отрезка по координатам его концов;

• вычислять длину вектора по его координатам;

• вычислять расстояние между двумя точками;

• составлять уравнение окружности и прямой и использовать их при решении задач;

• вычислять значения синуса,косинусе,тангенса,котангенса углов от0до180°,применятьформулы приведения;

• применять теорему о площади треугольника при решении задач;

• применять теорему синусов при решении задач;

• применять теорему синусов при решении задач;

• решать треугольник;

• вычислять скалярное произведение векторов по его определению и по координатам векторов;

• применять формулы для вычисления углов,сторон,периметра и площади правильного мно-гоугольника, его радиуса вписанной и описанной окружностей

• применять формулы для вычисления длины окружности и дуги окружности;

• применять формулы для вычисления площади круга и кругового сектора;

• применять свойства движений при решении задач;

• применять формулы для вычисления площадей поверхностей и объемов многогранников ител вращения;

Выпускники получат возможность научиться:

• применять координатный метод при доказательстве теорем и решении задач;

• строить образы геометрических фигур при движении;

• решать задачи повышенного уровня сложности;

• владеть различными способами и методами решения планиметрических задач;

• находить решения«жизненных» (компетентностных)задач,в которых используются матема-тические средства;

• создавать продукт(результат проектной деятельности),для изучения и описания которогоиспользуются математические средства.

МЕТАПРЕДМЕТНЫЕ

Регулятивные

По окончании изучения курса выпускник научится:

1. первоначальные представления об идеях и о методах математики как универсальном языке

науки и техники, средстве моделирования явлений и процессов;

1. умение видеть математическую задачу в контексте проблемной ситуации в других дисци-плинах, в окружающей жизни;

1. умение находить в различных источниках информацию, необходимую для решения матема-тических проблем, представлять ее в понятной форме, принимать решение в условиях не-полной и избыточной, точной и вероятностной информации;

1. умение понимать и использовать математические средства наглядности (графики, диаграм-мы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;

Выпускники получат возможность научиться:

1. умение выдвигать гипотезы при решении учебных задач, понимать необходимость их про-верки;

1. умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;

1. понимание сущности алгоритмических предписаний и умение действовать в соответствии с

предложенным алгоритмом;

1. умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

1. умение планировать и осуществлять деятельность, направленную на решение задач исследо-вательского характера;

Познавательные

По окончании изучения курса выпускник научится:

1. выделять существенное и несущественное в тексте задачи, составлять краткую запись условия задачи;

o моделировать условия текстовых задач освоенными способами;

o устанавливать закономерности и использовать их при выполнении заданий(продолжать ряд,заполнять пустые клетки в таблице, составлять равенства и решать задачи по аналогии);

o осуществлять синтез числового выражения(восстановление деформированных равенств),усло-вия текстовой задачи (восстановление условия по рисунку, схеме, краткой записи);

o конструировать геометрические фигуры из заданных частей,достраивать часть до заданнойгеометрической фигуры, мысленно делить геометрическую фигуру на части;

o сравнивать и классифицировать числовые и буквенные выражения,текстовые задачи,геомет-рические фигуры по заданным критериям;

o понимать информацию,представленную в виде текста,схемы,таблицы,дополнять таблицынедостающими данными, находить нужную информацию в учебнике.

Выпускники получат возможность научиться: o моделировать условия текстовых задач, o решать задачи разными способами;

o устанавливать причинно-следственные связи,строить логическое рассуждение,проводить ана-логии и осваивать новые приёмы вычислений, способы решения задач;

o проявлять познавательную инициативу при решении конкурсных задач;

o выбирать наиболее эффективные способы вычисления значения конкретного выражения;

o сопоставлять информацию,представленную в разных видах,обобщать её,использовать привыполнении заданий, переводить информацию из одного вида в другой, находить нужную информацию в детской энциклопедии, Интернете.

Коммуникативные

По окончании изучения курса выпускник научится:

1. сотрудничать с товарищами при выполнении заданий в паре: устанавливать очерёдность дей-

ствий;

o осуществлять взаимопроверку;

o обсуждать совместное решение(предлагать варианты,сравнивать способы вычисления или ре-шения задачи);

o объединять полученные результаты(при решении комбинаторных задач); o задавать вопросы с целью получения нужной информации.

Выпускники получат возможность научиться:

o учитывать мнение партнёра,аргументировано критиковать допущенные ошибки,обосновыватьсвоё решение;

o выполнять свою часть обязанностей в ходе групповой работы,учитывая общий план действий

• конечную цель;

1. задавать вопросы с целью планирования хода решения задачи, формулирования познаватель-ных целей в ходе проектной деятельности.

ГЕОМЕТРИЯ

Геометрические фигуры

По окончании изучения курса выпускник научится:

 Пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;

• Распознавать и изображать на чертежах и рисунках геометрические фигуры и их комбинации;

• Классифицировать геометрические фигуры;

• Находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 0 до 180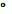 , применяя определения, свойства и признаки фигур и их элементов, отношения фигур (равен-ство, подобие, симметрия, поворот, параллельный перенос);

• Оперировать с начальными понятиями тригонометрии и выполнять элементарные операции над функциями углов;

• Доказывать теоремы;

• Решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательства;

• Решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;

• Решать простейшие планиметрические задачи.

Выпускник получит возможность научиться:

• Овладеть методами решения задач на вычисление и доказательство: методом от противного, мето-дом подобия, методом перебора вариантов и методом геометрических мест точек;

• Приобрести опыт применения алгебраического и тригонометрического аппарата и идей движения при решении геометрических задач;

• Овладеть традиционной схемой решения задач на построение с помощью циркуля и линейки: ана-лиз, построение, доказательство и исследование;

• Научиться решать задачи на построение методом геометрических мест точек и методом подобия;

• Приобрести опыт исследования свойств планиметрических фигур с помощью компьютерных про-грамм;

• Приобрести опыт выполнения проектов.

Измерение геометрических величин

По окончании изучения курса выпускник научится:

• Использовать свойства измерения длин, углов и площадей при решении задач на нахождение дли-ны отрезка, длины окружности, длины дуги окружности, градусной меры угла;

• Вычислять площади треугольников, прямоугольников, трапеций, кругов и секторов;

• Вычислять длину окружности и длину дуги окружности;

• Вычислять длины линейных элементов фигур и их углы, используя изученные формулы, в том числе формулы длины окружности и длины дуги окружности, формулы площадей фигур;

• Решать задачи на доказательство с использованием формул длины окружности и длины дуги окружности, формул площадей фигур;

• Решать практические задачи, связанные с нахождением геометрических величин( используя при необходимости справочники и технические средства).

Выпускник получит возможность научиться:

• Вычислять площади фигур, составленных из двух или более прямоугольников, параллелограммов, треугольников, круга и сектора;

• Вычислять площади многоугольников, используя отношения равновеликости и равносоставленно-сти.

• Применять алгебраический и тригонометрический аппарат и идеи движения при решении задач на вычисление площадей многоугольников.

Координаты

По окончании изучения курса выпускник научится:

• Вычислять длину отрезка по координатам его концов; вычислять координаты середины отрезка;

• Использовать координатный метод для изучения свойств прямых и окружностей.

Выпускник получит возможность научиться:

• Овладеть координатным методом решения задач на вычисление и доказательство;

• Приобрести опыт использования компьютерных прогамм для анализа частных случаев взаимного расположения окружностей и прямых;

• Приобрести опыт выполнения проектов.

Векторы

По окончании изучения курса выпускник научится:

• Оперировать с векторами: находить сумму и разность двух векторов, заданных геометрически, находить вектор, равный произведению заданного вектора на число;

• Находить для векторов, заданных координатами: длину вектора, координаты суммы и разности двух и более векторов, координаты произведения вектора на число, применяя при необходимости переместительный, сочетательный или распределительный законы;

• Вычислять скалярное произведение векторов, находить угол между векторами, устанавливать пер-пендикулярность прямых.

Выпускник получит возможность научиться:

• Овладеть векторным методом для решения задач на вычисление и доказательство;

• Приобрести опыт выполнения проектов.

СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА

Векторы (8 часов)

Понятие вектора.Равенство векторов.Откладывание вектора от данной точки.Сумма двухвекторов. Законы сложения векторов. Вычитание векторов. Произведения вектора на число. Примене-ние векторов к решению задач.

Метод координат (10 часов)

Разложение вектора по двум неколлинеарным векторам.Координаты вектора.Связь между координатами вектора и координатами его начала и конца. Простейшие задачи в коорди-натах. Уравнение окружности. Уравнение прямой. Взаимное расположение двух окружностей. Метод координат к решению задач.

Соотношения между сторонами и углами треугольника.

Скалярное произведение векторов (11часов)

Си-нус, косинус, тангенс, котангенс угла. Основное тригонометрическое тождество. Формулы приведе-ния. Формулы для вычисления координат точки. Теорема о площади треугольников. Теорема синусов. Теорема косинусов. Решение треугольников. Измерительные работы. Скалярное произведение векто-ров. Скалярное произведение в координатах. Свойство скалярного произведения.

Правильные многоугольники. Длина окружности и площадь круга (12 часов)

Правильный многоугольник.Окружность, вписанная в правильного многоугольника. Окружность, описанная около правильный многоугольник Формулы для вычисления площади правильного многоугольника, его стороны и ра-диуса вписанной окружности. Длина окружности. Длина дуги. Площадь круга. Площадь кругового сектора.

Движения (8 часов)

Понятие движения.Отображение плоскости на себя.Понятие движения.Параллельныйперенос. Поворот.

Начальные сведения из стереометрии( 8 часов)

Предмет стереометрии.Многогранник.Призма.Параллеле-пипед. Свойства прямоугольного параллелепипеда. Объём тела. Пирамида. Цилиндр. Конус. Сфера и шар.

Обобщающее повторение (7 часов)