ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Дисциплина «Математика» является одной из обязательных дисциплин общеобразовательного цикла подготовки квалифицированного работника по профессии 23.01.08. слесарь по ремонту строительных машин.
Примерная программа по учебным предметам геометрия и алгебра и начала математического анализа, 10 – 11 классы составлена на основании: Закона Донецкой Народной Республики «Об образовании» (принят Постановлением Народного Совета 19 июня 2015 года, с изменениями, внесенными Законами от 04.03.2016 № 111-IНС, от 03.08.2018 № 249-IНС от 12.06.2019 № 41-IIНС, от 18.10.2019 № 64-IIНС, от 13.12.2019 № 75-IIНС, от 06.03.2020 № 107-IIНС, от 27.03.2020 № 116-IIНС); Государственного образовательного стандарта среднего общего образования Донецкой Народной Республики, утвержденного приказом Министерства образования и науки Донецкой Народной Республики от 07.08.2020 г. № 121-НП, в соответствии с требованиями Примерной основной образовательной программы основного общего образования Донецкой Народной Республики в редакции 2020 года, с учетом учебно-методического комплекса Л.А. Атанасян и др. «Геометрия, 10-11» и с учетом учебно-методического комплекса Ш.А.Алимов и др. «Алгебра и начала математического анализа, 10-11».
Геометрия – один из важнейших компонентов математического образования, она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции, математической культуры и эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления и формирование понятия доказательства.
В базовом курсе геометрия содержание образования развивается в следующих направлениях:
расширение системы сведений о свойствах плоских фигур, систематическое изучение свойств пространственных тел, развитие представлений о геометрических измерениях;
совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
Примерные программы по курсу алгебры и математического анализа выполняют две основные функции:
информационно-методическую функцию, которая позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитании и развитии обучающихся средствами данного учебного предмета;
организационно-планирующую функцию, предусматривающую выделение этапов обучения, структурирование учебно-методического материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации обучающихся.
При изучении курса алгебры и начал математического анализа продолжаются и получают развитие содержательные линии:«Числа и вычисления», «Выражения и их преобразования», «Функции», «Уравнения и неравенства, системы», «Арифметическая и геометрическая прогрессии», «Элементы комбинаторики, теории вероятностей и статистики».Вводится новая тематическая линия «Начала математического анализа».
Изучение курса алгебры и начал математического анализа направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для последующего обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
воспитание культуры личности средствами математики: понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
Изучение курса геометрии на базовом уровне среднего общего образования направлено на достижение следующих целей:
системное и осознанное усвоение курса геометрии;
формирование математического стиля мышления, включающего в себя индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию;
развитие интереса обучающихся к изучению геометрии;
использование математических моделей для решения прикладных задач, задач из смежных дисциплин;
приобретение опыта осуществления учебно-исследовательской, проектной и информационно-познавательной деятельности;
развитие индивидуальности и творческих способностей, направленное на подготовку выпускников к осознанному выбору профессии.
В рамках указанных содержательных линий курса алгебры и начал математического анализа решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование техники вычислений, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и прикладных задач;
развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств и их систем;
расширение и систематизация сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей,
знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать функции и решать геометрические, физические и другие прикладные задачи;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
приобретение опыта математической деятельности, позволяющего свободно применять изученные факты и методы при решении задач различных разделов курса, а также использовать их в нестандартных ситуациях;
формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
В соответствии с принятой Концепцией развития математического образования в Донецкой Народной Республике, математическое образование решает, в частности, следующие ключевые задачи:
«предоставлять каждому обучающемуся возможность достижения уровня математических знаний, необходимого для дальнейшей успешной жизни в обществе»;
«обеспечивать необходимое стране число выпускников, математическая подготовка которых достаточна для продолжения образования в различных направлениях и для практической деятельности, включая преподавание математики, математические исследования, работу в сфере информационных технологий и др.»;
«в основном общем и среднем общем образовании необходимо предусмотреть подготовку обучающихся в соответствии с их запросами к уровню подготовки в сфере математического образования».
Соответственно, выделяются три направления требований к результатам математического образования:
практико-ориентированное математическое образование (математика для жизни);
математика для использования в профессии;
творческое направление, на которое нацелены те обучающиеся, которые планируют заниматься творческой и исследовательской работой в области математики, физики, экономики и других областях.
При изучении курса алгебры и начал математического анализам продолжаются и получают развитие содержательные линии:«Числа и вычисления», «Выражения и их преобразования», «Функции», «Уравнения и неравенства, системы», «Арифметическая и геометрическая прогрессии», «Элементы комбинаторики, теории вероятностей и статистики».Вводится новая тематическая линия «Начала математического анализа».
В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование техники вычислений, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и прикладных задач;
развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств и их систем;
расширение и систематизация сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей,
знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать функции и решать геометрические, физические и другие прикладные задачи;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
приобретение опыта математической деятельности, позволяющего свободно применять изученные факты и методы при решении задач различных разделов курса, а также использовать их в нестандартных ситуациях;
формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
Цели освоения программы базового уровня – обеспечение возможности использования математических знаний и умений в повседневной жизни и возможности успешного продолжения образования по специальностям, не связанным с прикладным использованием математики.
Обучающиеся, осуществляющие обучение на базовом уровне, должны освоить общие математические умения, необходимые для жизни в современном обществе; вместе с тем они получают возможность изучить предмет глубже, с тем, чтобы в дальнейшем при необходимости изучать математику для профессионального применения. При изучении математики большое внимание уделяется развитию коммуникативных умений (формулировать, аргументировать и критиковать), формированию основ логического мышления в части проверки истинности и ложности утверждений, построения примеров и контрпримеров, цепочек утверждений, формулировки отрицаний, а также необходимых и достаточных условий. В зависимости от уровня программы больше или меньше внимания уделяется умению работать по алгоритму, методам поиска алгоритма и определению границ применимости алгоритмов. Требования, сформулированные в разделе «Геометрия», в большей степени относятся к развитию пространственных представлений и графических методов, чем к формальному описанию стереометрических фактов.
Выпускник научится: для использования в повседневной жизни и обеспечения возможности успешного продолжения образования по специальностям, не связанным с прикладным использованием математики.
Выпускник получит возможность научиться: для развития мышления, использования в повседневной жизни и обеспечения возможности успешного продолжения образования по специальностям, не связанным с прикладным использованием математики.
В основе программы дисциплины лежат следующие нормативные документы:
Закон Донецкой Народной Республики "Об образовании" (принят Постановлением Народного Совета 19 июня 2015 года, с изменениями, внесенными Законами от 04.03.2016 № 111-IНС, от 03.08.2018 № 249-IНС от 12.06.2019 № 41-IIНС, от 18.10.2019 № 64-IIНС, от 13.12.2019 № 75-IIНС, от 06.03.2020 № 107-IIНС, от 27.03.2020 № 116-IIНС);
Государственный образовательный стандарт среднего общего образования Донецкой Народной Республики, утвержденный приказом Министерства образования и науки Донецкой Народной Республики от 07.08.2020 г. № 121-НП;
Примерная основная образовательная программа среднего общего образования Донецкой Народной Республики в редакции 2020 года;
Приказ МОН ДНР № 328 от 20.07.2015 г «О порядке организации и осуществления образовательной деятельности по образовательным программам среднего профессионального образования»;
Учебный план по профессии: 08.01.06 (Мастер сухого строительства).
1. ПАСПОРТ РАБОЧЕЙ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ «математика»
1.1.Область применения программы
Рабочая программа учебной дисциплины "Математика" является частью программы подготовки квалифицированных рабочих и служащих ГПОУ «Макеевский строительный центр профессионально-технического образования имени Ф.И.Бачурина» в соответствии с ГОС СПО по специальности: 23.01.08. Слесарь по ремонту строительных машин
1.2.Место дисциплины в структуре программы подготовки квалифицированных рабочих, служащих
Учебная дисциплина «Математика» относится к обязательной части общеобразовательного цикла ППКРС.
1.3. Цели и задачи учебной дисциплины - требования к результатам освоения учебной дисциплины
Изучение геометрии по данной программе способствует формированию у обучающихся личностных, метапредметных, предметных результатов обучения, соответствующих требованиям образовательного стандарта среднего (полного) общего образования.
Личностные результаты:
1)воспитание гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада учёных Донбасса в развитие мировой науки;
2) формирование мировоззрения, соответствующего современному уровню развития науки и общественной практики;
3) ответственное отношение к обучению, готовность и способность к саморазвитию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
4) осознанный выбор будущей профессиональной деятельности на базе ориентирования в мире профессий и профессиональных предпочтений; отношение к профессиональной деятельности как к возможности участия в решении личных, общественных, государственных и общенациональных проблем; формирование уважительного отношения к труду; развитие опыта участия в социально значимом труде;
5) умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности;
6) умение управлять своей познавательной деятельностью;
7) умение взаимодействовать с одноклассниками, детьми младшего возраста и взрослыми в образовательной, общественно-полезной, учебно-исследовательской, проектной и других видах деятельности;
8) критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
1) умение самостоятельно определять цели своей деятельности, ставить и формулировать для себя новые задачи в учёбе;
2) умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
3) умение самостоятельно принимать решения, проводить анализ своей деятельности, применять различные методы познания;
4) владение навыками познавательной, учебно-исследовательской и проектной деятельности;
5) формирование понятийного аппарата, умения создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
6) умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
7) формирование компетентности в области использования информационно-коммуникационных технологий;
8) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
9) умение самостоятельно осуществлять поиск в различных источниках, отбор, анализ, систематизацию и классификацию информации, необходимой для решения математических проблем, представлять её в понятной форме; принимать решение в условиях неполной или избыточной, точной или вероятностной информации; критически оценивать и интерпретировать информацию, получаемую из различных источников;
10) умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
11) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
12) умение использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации.
Предметные результаты:
1) осознание значения математики для повседневной жизни человека;
2) представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
3) умение описывать явления реального мира на математическом языке; представление о математических понятиях и математических моделях как о важнейшем инструментарии, позволяющем описывать и изучать разные процессы и явления;
4) представление об основных понятиях, идеях и методах геометрии;
5) владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
6) практически значимые математические умения и навыки, способность их применения к решению математических и нематематических задач.
7) владение навыками использования компьютерных программ при решении математических задач;
8) практически значимые математические умения и навыки, способность их применения к решению математических и нематематических задач, предполагающие умения:
выполнять вычисления с действительными числами;
- решать рациональные, иррациональные, показательные, логарифмические, степенные и тригонометрические уравнения, системы уравнений;
- решать рациональные, иррациональные, показательные, логарифмические, степенные и тригонометрические неравенства, системы неравенств;
- решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений, систем уравнений и неравенств;
- использовать алгебраический «язык» для описания предметов окружающего мира и создания соответствующих математических моделей;
- выполнять тождественные преобразования рациональных, иррациональных, показательных, логарифмических, степенных, тригонометрических выражений;
- выполнять операции над множествами;
- исследовать функции с помощью производной и строить их графики;
- вычислять площади фигур и объёмы тел с помощью определённого интеграла;
- проводить вычисление статистических характеристик, выполнять приближённые вычисления;
- решать комбинаторные и вероятностные задачи.
1.4. Количество часов, отведенное на освоение программы учебной дисциплины:
Максимальной учебной нагрузки обучающегося – 383 часов, в том числе:
обязательной аудиторной учебной нагрузки обучающегося - 333 часов;
самостоятельной работы обучающегося - 50 часов.
2. СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
2.1. Объем учебной дисциплины и виды учебной работы
| Вид учебной работы | Объем часов |
| Максимальная учебная нагрузка (всего) | 383 |
| Обязательная аудиторная учебная нагрузка (всего) | 333 |
| в том числе: |
|
| лабораторные занятия (не предусмотрено) | - |
| практические занятия | - |
| контрольные работы | 33 |
| Самостоятельная работа обучающегося (всего) | 50 |
| в том числе: |
|
| индивидуальные задания творческого характера |
|
| домашняя индивидуальная работа |
|
| работа над конспектом лекций |
|
| работа над учебной литературой |
|
| Итоговая аттестация в форме экзамен |
2.2. Тематический план и содержание учебной дисциплины Математика
| Наименование разделов и тем | Содержание учебного материала, лабораторные и практические работы, самостоятельная работа обучающихся, курсовая работ (проект) (если предусмотрены) | Объем часов | Уровень освоения |
| 1 | 2 | 3 | 4 |
| Тема 1. Обобщение и систематизация материала. | 1. Дроби. Действия с дробями. | 1 | 1 |
| 2.Тождественные преобразования выражений. Формулы сокращенного умножения. | 1 | 1 |
| 3. Степень, свойства степени Квадратный корень, его свойства | 1 | 1 |
| 4. Неравенства, их системы. Метод интервалов при решении нелинейных неравенств |
|
|
| 5. Контрольная работа (диагностическая) | 1 | 3 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) | 1 |
|
| Тема 2. Действительные числа. | 1. Целые и рациональные числа. | 2 | 2 |
| 2. Действительные числа | 1 | 2 |
| 3. Бесконечно убывающая геометрическая прогрессия | 1 | 2 |
| 4. Арифметический корень натуральной степени | 2 | 2 |
| 5. Степень с рациональным и действительным показателем | 3 | 2 |
| 6. Решение задач | 3 | 2 |
| 7. Контрольная работа по теме «Действительные числа» | 1 | 3 |
| 8. Анализ контрольной работы | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Действительные числа» | 2
1 |
|
| Тема 3. Введение в предмет стереометрии | 1. Основные понятия стереометрии. Аксиомы стереометрии. | 1 | 2 |
| 2. Некоторые следствия из аксиом. | 1 | 2 |
| Тема 4. Параллельность прямых и плоскостей. | 1. Параллельность прямых, прямой и плоскости. | 2 | 1 |
| 2. Параллельность прямой и плоскости. | 2 | 2 |
| 3. Взаимное расположение прямых в пространстве. Угол между двумя прямыми. | 1 | 2 |
| 4. Параллельность плоскостей. | 2 | 2 |
| 5. Контрольная работа №1 по теме «Параллельность прямых и плоскостей» | 1 | 3 |
| 6. Тетраэдр | 2 | 2 |
| 7. Параллелепипед. | 2 | 2 |
| 8. Решение задач. | 1 | 2 |
| 9. Контрольная работа№2 по теме «Параллельность прямых и плоскостей» | 1 | 3 |
| Анализ контрольной работы. | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Параллельность прямых, прямой и плоскости, плоскостей в пространстве») |
2
|
|
| Тема 5. Степенная функция. | 1. Степенная функция, ее свойства и график | 2 | 2 |
| 2. Взаимно обратные функции | 1 | 2 |
| 3. Равносильные уравнения. | 2 | 2 |
| 4. Равносильные уравнения. | 2 | 2 |
| 5. Равносильные неравенства | 2 | 2 |
| 6. Решение задач | 2 | 2 |
| 7. Контрольная работа по теме «Степенная функция» | 1 | 3 |
| 8. Анализ контрольной работа | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Рациональные уравнения и неравенства») |
2
|
|
| Тема 6. Показательная функция | 1. Показательная функция, ее свойства и график | 2 | 2 |
| 2. Показательные уравнения | 2 | 2 |
| 3. Показательные уравнения | 2 | 2 |
| 4. Контрольная работа №1 по теме «Показательная функция» | 1 | 3 |
| 5. Показательные неравенства | 2 | 2 |
| 6. Системы показательных уравнений и неравенств | 2 | 2 |
| 7. Решение задач | 2 | 2 |
| 8. Контрольная работа №2 по теме «Показательная функция» | 1 | 3 |
| 9. Анализ контрольной работа | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Арифметический корень» |
2
|
|
| Тема 7. Перпендикулярность прямых и плоскостей | 1. Перпендикулярные прямые в пространстве. | 1 | 2 |
| 2. Перпендикулярность прямой и плоскости. | 2 | 2 |
| 3. Признак перпендикулярности прямой и плоскости. | 2 | 2 |
| 4. Перпендикуляр и наклонная. Расстояние от точки до плоскости. | 2 | 2 |
| 5. Теорема о трех перпендикулярах. | 2 | 2 |
| 6. Угол между прямой и плоскостью. | 2 | 2 |
| 7. Контрольная работа №1 по теме «Перпендикулярность прямых и плоскостей» | 1 | 3 |
| 8. Анализ контрольной работы. | 1 | 2 |
| 9. Двугранный угол. | 2 | 2 |
| 10. Перпендикулярность плоскостей. | 2 | 2 |
| 11. Признак перпендикулярности плоскостей. | 2 | 2 |
| 12. Прямоугольный параллелепипед. | 2 | 2 |
| 13. Урок обобщения и систематизации знаний | 2 | 2 |
| 14. Контрольная работа №2 по теме «Перпендикулярность прямых и плоскостей» | 1 | 3 |
| 15. Анализ контрольной работы. | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Показательная функция» |
3
|
|
| Тема 8. Логарифмическая функция. | 1. Логарифмы | 1 | 2 |
| 2. Свойства логарифмов | 2 | 2 |
| 3. Десятичные и натуральные логарифмы | 1 | 2 |
| 4. Логарифмическая функция, ее свойства и график | 2 | 2 |
| 5. Логарифмические уравнения | 2 | 2 |
| 6. Логарифмические неравенства | 2 | 2 |
| 7. Решение задач | 1 | 2 |
| 8. Контрольная работа по теме «Логарифмическая функция» | 1 | 3 |
| 9. Анализ контрольной работы | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Перпендикулярность прямых, прямой и плоскости, плоскостей» |
2 |
|
| Тема 9. Тригонометрические формулы. | Радианная мера угла | 1 | 2 |
| Поворот точки вокруг начала координат | 1 | 2 |
| Определение синуса, косинуса тангенса | 1 | 2 |
| Знаки синуса, косинуса тангенса | 1 | 2 |
| Зависимость между синусом, косинусом, тангенсом одного и того же угла | 2 | 2 |
| Тригонометрические тождества | 2 | 2 |
| Контрольная работа №1 по теме «Тригонометрические формулы» | 1 | 3 |
| Синус, косинус тангенс углов  и и 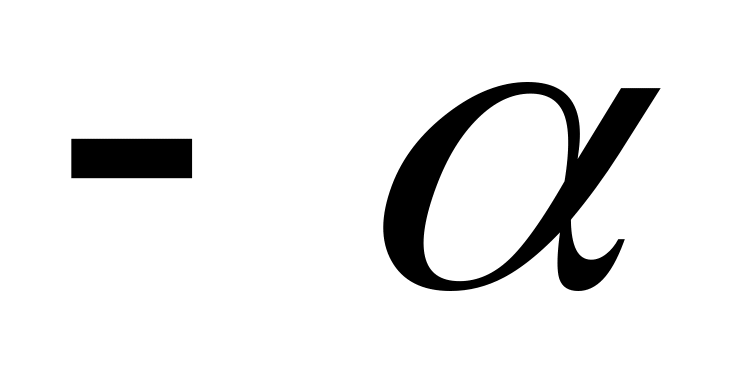 | 2 | 2 |
| Формулы сложения | 2 | 2 |
| Синус, косинус и тангенс двойного угла | 2 | 2 |
| Формулы приведения | 2 | 2 |
|
| Формулы приведения | 2 | 2 |
| Контрольная работа №2 по теме «Тригонометрические формулы» | 1 | 3 |
| Сумма и разность синусов. | 2 | 2 |
| Сумма и разность косинусов | 2 | 2 |
| Решение задач. | 2 | 2 |
| Контрольная работа по теме «Тригонометрические формулы» | 1 | 3 |
| Анализ контрольной работы | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) | 3
|
|
|
|
|
|
|
|
| Обязательная аудиторная нагрузка – 120 из нее Самостоятельная работа – 17, контрольная работа - 12 |
|
|
|
| II - курс |
|
|
| Тема 1. Обобщение и систематизация материала. | 1. Действительные числа 2. Степенная функция, ее свойства и график 3. Показательные уравнения и неравенства 4. Логарифмические уравнения и неравенства. 5. Диагностическая контрольная работа | 1 1 1 1 1 | 2 2 2 2 3 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем. | 1 |
|
| Тема 2. Тригонометрические уравнения. | Уравнение 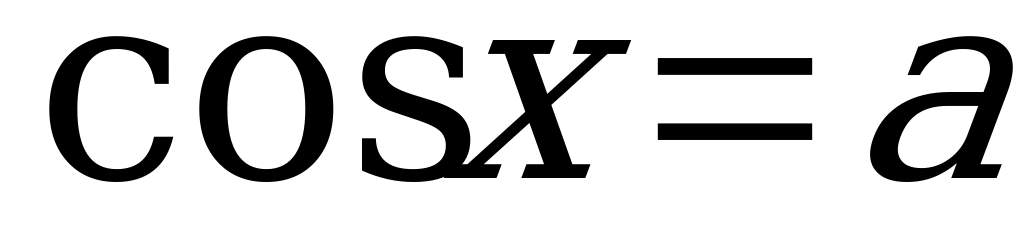 | 2 | 2 |
| Уравнение 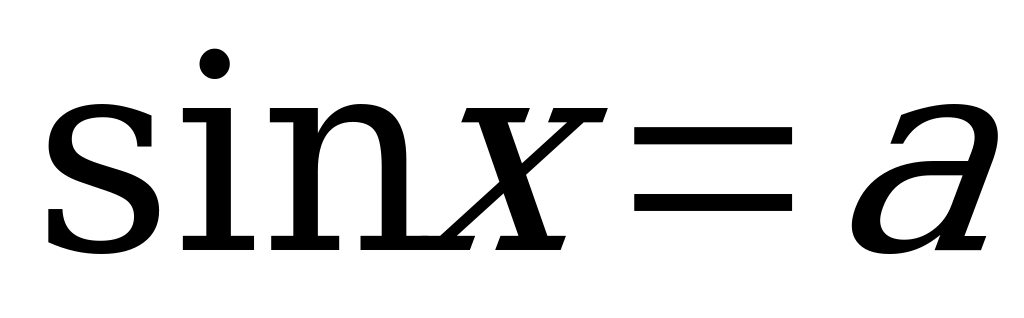 | 2 | 2 |
| Уравнения 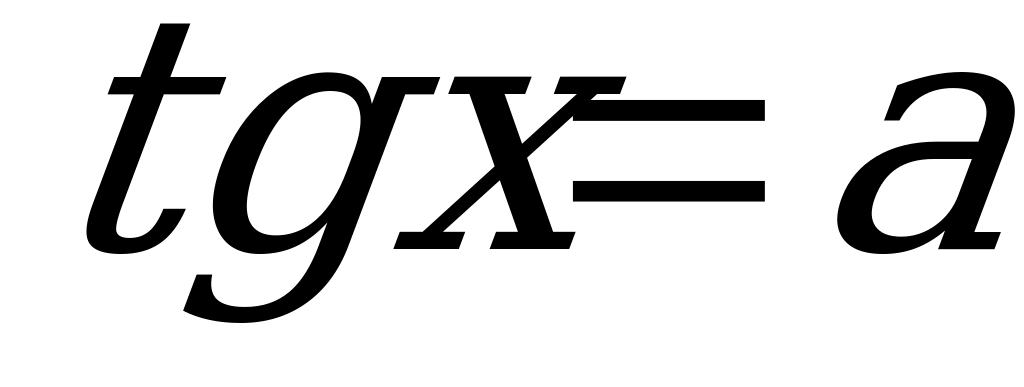 | 2 | 2 |
| Решение тригонометрических уравнений | 2 | 2 |
| Решение уравнений. | 2 | 2 |
| Контрольная работа по теме «Тригонометрические уравнения» | 1 | 3 |
| Анализ контрольной работы | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Призма», «Пирамида», «Параллелепипед», «Правильные многогранники» | 2 |
|
| Тема 3. Тригонометрические функции. | Область определения и множество значений тригонометрических функций | 1 | 2 |
| Четность, нечетность, периодичность тригонометрических функций | 1 | 2 |
| Свойства функции 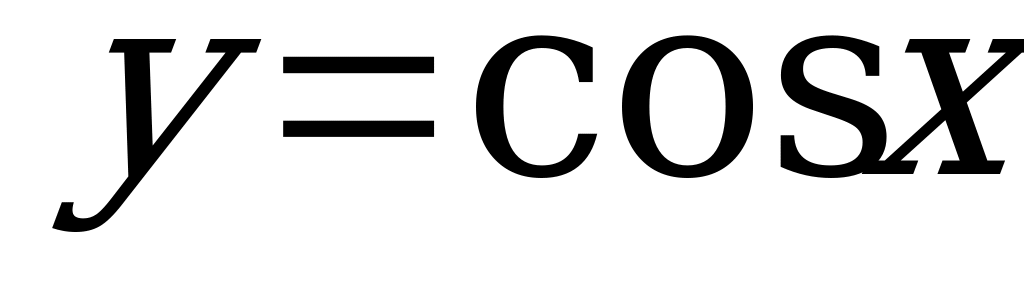 и ее график и ее график | 2 | 2 |
| Свойства функции 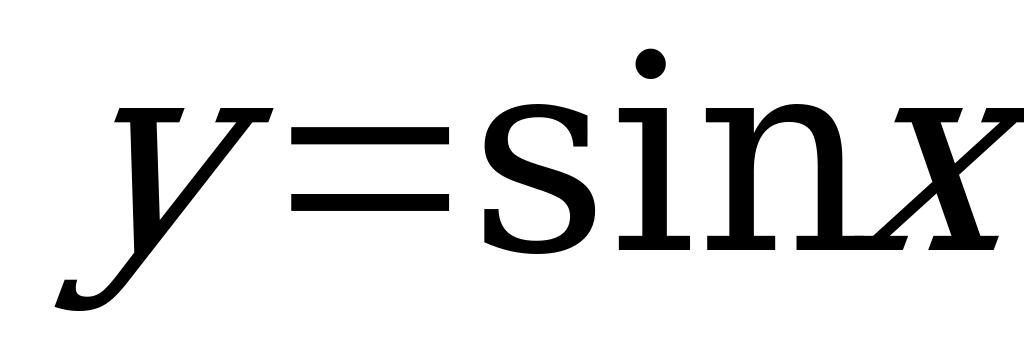 и ее график и ее график | 2 | 2 |
| Свойства функций 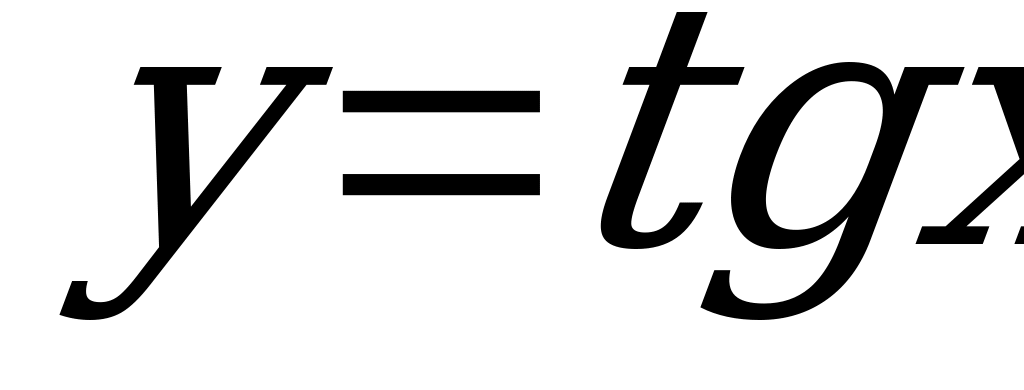 и её график и её график | 1 | 2 |
| Решение задач | 2 | 2 |
| Контрольная работа по теме «Тригонометрические функции» | 1 | 3 |
| Анализ контрольной работы | 1 | 1 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Показательная функция», «Решение показательных уравнений», «Решение показательных неравенств». | 2 |
|
| Тема 4. Векторы в пространстве | Понятие вектора в пространстве | 1 | 2 |
| Равенство векторов. | 2 | 2 |
| Сложение и вычитание векторов. | 2 | 2 |
| Умножение вектора на число | 2 | 2 |
| Компланарные векторы | 2 | 2 |
| Решение задач | 2 | 2 |
| Контрольная работа по теме «Векторы в пространстве» | 1 | 3 |
| Анализ контрольной работы. | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «векторы в пространстве». |
2 |
|
| Тема 5. Метод координат. Движение. | Прямоугольная система координат в пространстве. | 2 | 2 |
| Координаты вектора. | 3 | 2 |
| Простейшие задачи в координатах. | 4 | 2 |
| Контрольная работа №1 по теме «Метод координат. Движение» | 1 | 3 |
| Скалярное произведение векторов. Угол между векторами. | 4 | 2 |
| Вычисление углов между прямыми и плоскостями. | 2 | 2 |
| Движения. | 2 | 2 |
| Контрольная работа №2 по теме «Метод координат. Движение» | 1 | 3 |
| Анализ контрольной работы. | 1 | 3 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Понятие производной», «Правила дифференцирования». |
2 |
|
| Тема 6. Многогранники. | Понятие многогранника. Призма. | 2 | 2 |
| Площадь полной поверхности призмы. | 2 | 2 |
| Правильная призма. | 2 | 2 |
| Пирамида. | 2 | 2 |
| Правильная пирамида. | 2 | 2 |
| Контрольная работа №1 по теме «Многогранники» | 1 | 3 |
| Усеченная пирамида. | 2 | 2 |
| Правильные многогранники | 1 | 2 |
| Элементы симметрии правильных многогранников | 1 | 2 |
|
| Решение задач. | 2 | 2 |
| Контрольная работа №2 по теме «Многогранники» | 1 | 3 |
| Анализ контрольной работы. | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) | 2
|
|
| Тема7. Производная и ее геометрический смысл. | Производная | 2 | 2 |
| Производная степенной функции | 2 | 2 |
| Правила дифференцирования | 4 | 2 |
| Производные некоторых элементарных функций | 3 | 2 |
| Контрольная работа №1 по теме «Производная и ее геометрический смысл» | 1 | 3 |
| Геометрический смысл производной | 2 | 2 |
| Уравнение касательной к графику функции | 2 | 2 |
| Решение упражнений. | 2 | 2 |
| Контрольная работа №2 по теме «Производная и ее геометрический смысл» | 1 | 3 |
| Анализ контрольной работы | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) Домашняя индивидуальная работа (составление презентации на тему: «Объем прямоугольного параллелепипеда.», «Объем прямой призмы», «Объем цилиндра», «Объем пирамиды», «Объем конуса», «Объем шара». |
2 |
|
| Тема 8. Применение производной функции. | Возрастание и убывание функции | 1 | 2 |
| Экстремумы функции | 2 | 2 |
| Применение производной к построению графиков функций | 2 | 2 |
| Наибольшее и наименьшее значения функции | 2 | 2 |
|
| Решение задач | 2 | 2 |
| Контрольная работа по теме «Применение производной функции» | 1 | 3 |
| Анализ контрольной работы | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) |
2 |
|
| Тема 9. Интеграл. | Первообразная | 1 | 2 |
| Правила нахождения первообразной | 2 | 2 |
| Площадь криволинейной трапеции и интеграл | 2 | 2 |
| Вычисление интегралов. Вычисление площадей с помощью интегралов | 2 | 2 |
| Решение задач | 2 | 2 |
| Контрольная работа по теме «Интеграл» | 1 | 3 |
| Анализ контрольной работы | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем)
| 2 |
|
| Тема 10. Повторение | Тригонометрические формулы. | 1 | 2 |
| Тригонометрические уравнения | 1 | 2 |
| Тригонометрические функции. | 1 | 2 |
| Векторы в пространстве. Скалярное произведение векторов | 1 | 2 |
| Производная и ее геометрический смысл. Итог. | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем)
| 1 |
|
|
| Обязательная аудиторная нагрузка – 129 час. из нее самостоятельная работа – 18, контрольная работа - 12 |
|
|
|
| III - курс |
|
|
| Тема 1. Обобщение и систематизация материала | Тригонометрические формулы | 1 | 2 |
| Тригонометрические уравнения | 1 |
|
| Тригонометрические функции | 1 | 2 |
| Векторы в пространстве | 1 | 2 |
| Диагностическая контрольная работа | 1 | 3 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем)
| 1
|
|
| Тема 2. Цилиндр, шар, конус | Цилиндр. | 2 | 2 |
| Площадь поверхности цилиндра. | 2 | 2 |
| Конус. | 2 | 2 |
| Площадь поверхности конуса. | 2 | 2 |
| Решение задач | 2 | 2 |
| Контрольная работа №1 по теме «Цилиндр, шар, конус» | 1 | 3 |
| Анализ контрольной работы | 1 | 2 |
| Усеченный конус. | 2 | 2 |
| Сфера и шар. | 2 | 2 |
| Уравнение и площадь сферы. | 1 | 2 |
| Взаимное расположение сферы и плоскости. | 1 | 2 |
| Решение задач | 2 | 2 |
| Контрольная работа №2 по теме «Цилиндр, шар, конус» | 1 | 3 |
| Анализ контрольной работы. | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) | 4
|
|
| Тема 3. Объемы тел. | Объём прямоугольного параллелепипеда. | 2 | 2 |
| Объём прямой и наклонной призмы. | 3 | 2 |
| Объём цилиндра. | 2 | 2 |
| Объём пирамиды. | 2 | 2 |
| Решение задач | 2 | 2 |
| Контрольная работа №1 по теме «Объемы тел» | 1 | 3 |
| Анализ контрольной работы | 1 | 2 |
| Объём конуса. | 2 | 2 |
| Объём шара и его частей. | 2 | 2 |
| Решение задач | 2 | 2 |
| Контрольная работа №2 по теме «Объемы тел» | 1 | 3 |
| Анализ контрольной работы. | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) | 4 |
|
|
Тема 7. Комбинаторика. Элементы теории вероятностей. Статистика. | Правило произведения | 1 | 2 |
| Перестановки. Размещения | 1 | 2 |
| Сочетания и их свойства | 1 | 2 |
| Бином Ньютона | 2 | 2 |
| Решение задач | 2 | 2 |
| Контрольная работа по теме «Комбинаторика» | 1 | 3 |
| Анализ контрольной работы. | 1 | 2 |
| События. Комбинации событий. Противоположное событие. | 1 | 2 |
| Вероятность события. Сложение вероятностей | 1 | 2 |
| Независимые события. Умножение вероятностей. | 1 | 2 |
| Статистическая вероятность. Случайные величины | 1 | 2 |
| Центральные тенденции. Меры разброса | 1 | 2 |
| Решение задач | 2 | 2 |
| Контрольная работа по теме «Комбинаторика. Элементы теории вероятностей. Статистика» | 1 | 3 |
| Анализ контрольной работы | 1 | 2 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) | 2 |
|
| Тема 8. Повторение. | Действительные числа | 1 | 2 |
| Степенная функция, ее свойства и график | 1 | 2 |
| Показательные уравнения и неравенства | 2 | 2 |
| Логарифмические уравнения и неравенства. | 2 | 2 |
| Параллельность прямых и плоскостей | 1 | 2 |
| Перпендикулярность прямых и плоскостей | 1 | 2 |
| Многогранники | 1 | 2 |
| Тела вращения | 1 | 2 |
| Тригонометрические формулы | 1 | 2 |
| Тригонометрические уравнения | 2 | 2 |
| Тригонометрические функции | 1 | 2 |
| Векторы в пространстве | 1 | 2 |
| Производная и ее геометрический смысл | 1 | 2 |
| Применение производной |
|
|
| Интеграл | 1 | 2 |
| Объемы тел вращения. | 2 | 2 |
| Объемы многогранников | 1 | 2 |
| Итоговая контрольная работа. | 2 | 3 |
| Итоговое занятие | 1 | 3 |
| Самостоятельная работа обучающихся - систематическая проработка конспектов занятий, учебной литературы (по вопросам к параграфам, заданиям, главам учебных пособий, составленным преподавателем) | 7 |
|
|
Обязательная аудиторная нагрузка – 90, из нее самостоятельная работа – 15, контрольная работа - 8 |
90 |
|
|
Всего: Обязательная аудиторная нагрузка – 333, из нее самостоятельная работа – 50, контрольная работа - 33 |
333 |
|
Для характеристики уровня освоения учебного материала используются следующие обозначения:
1. – ознакомительный (узнавание ранее изученных объектов, свойств);
2. - репродуктивный (выполнение деятельности по образцу, инструкции или под руководством);
13. – продуктивный (планирование и самостоятельное выполнение деятельности, решение проблемных задач).
3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ ДИСЦИПЛИНЫ
3.1. Требования к минимальному материально-техническому обеспечению
Реализация программы дисциплины требует наличия учебного кабинета математики.
Оборудование учебного кабинета:
- рабочие места на 25-30 обучающихся;
- рабочее место преподавателя;
- комплекты демонстрационных таблиц по темам:
"Алгебра и начала анализа 10 кл.";
"Алгебра и начала анализа 11 кл.";
"Комбинаторика";
"Тригонометрические функции";
"Производная и ее применение";
"Теория вероятностей и математическая статистика";
- комплект инструментов для работы у доски;
- комплект моделей геометрических тел;
- комплект дидактических материалов обучающего и контролирующего характера по разделам дисциплины.
3.2. Информационное обеспечение обучения
Основные источники:
1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. «Геометрия 10-11 класс: учеб. для общеобразовательных организаций: базовый и углубленный уровень». – М.: Просвещение, 2016.
2. Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 10 класса. – М.: Просвещение, 2004.
3. Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 11 класса. – М.: Просвещение, 2004.
Зив Б.Г., Мейлер В.М., Баханский А.П. Задачи по геометрии для 7 – 11 классов. – М.: Просвещение, 2004.
4. Саакян С.М., Бутузов В.Ф. Изучение геометрии в 10 – 11 классах: Методические рекомендации к учебнику. Книга для учителя. – М.: Просвещение, 2003.
5. Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь. 10 класс. – М., Просвещение, 2013.
6. Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь. 11 класс. – М., Просвещение, 2013.
7. Литвиненко В.Н. Готовимся к ЕГЭ. 10 класс. – М., Просвещение, 2011.
8. Литвиненко В.Н. Готовимся к ЕГЭ. 11 класс. – М., Просвещение, 2012.
9. Федченко Л.Я., Литвиненко Г.Н.Разноуровневые задания для тематических и итоговых контрольных работ по геометрии. 10-11 классы.- Д., 2008.
10. Потемкин В.Л., Потемкина Л.Л. Геометрия. 10 – 11 классы. Задачник – практикум. – Д., 2017г.
11. Государственный образовательный стандарт среднего общего образования.
12. Алимов Ш.А. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10-11 классы: учеб.для общеобразовательных организаций: базовый и углубленный уровень / Ш.А.Алимов, Ю.М. Колягин и др. – М.: Просвещение, 2016.
13. Дидактические материалы по алгебре и началам анализа: кн. для обучающихся 10 кл. / М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, Р.Г. Газарян. – М.: Просвещение, 2005.
14. Дидактические материалы по алгебре и началам анализа: кн. для обучающихся 11 кл. / М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, Р.Г. Газарян. – М.: Просвещение, 2005.
15. Ткачева М.В. Алгебра и начала математического анализа. Тематические тесты. 10 класс / М.В. Ткачева, Н.Е. Федорова. − М.: Просвещение, 2011.
16. Ткачева М.В. Алгебра и начала математического анализа. Тематические тесты. 11 класс / М.В. Ткачева, Н.Е. Федорова. − М.: Просвещение, 2011.
17. Ткачёва М.В. Алгебра и начала математического анализа. Методические рекомендации. 10-11 класс: пособие для учителей общеобразовательных организаций / М.В. Ткачева, Н.Е. Федор. − М.: Просвещение, 2011.
18. Федченко Л.Я. Разноуровневые задания для тематических и итоговых контрольных работ по алгебре и началам анализа. 10-11 классы / Л.Я.Федченко. – Донецк, 2008.
19. Потемкина Л.Л., Потемкин В.Л. Алгебра и начала анализа 10 – 11 классы. Задачник – практикум / В.Л.Потемкин, Л.Л.Потемкина. – Донецк, 2017.
20. Федченко Л.Я., ПолищукИ.В., Потёмкина Л.Л. Алгебра и начала анализа 10 – 11кл. «Приложения к программам среднего общего образования», Донецк, 2017.
4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ ДИСЦИПЛИНЫ
Контроль и оценка результатов освоения дисциплины осуществляется преподавателем на аудиторных занятиях в процессе проведения письменных и устных опросов обучающихся, контрольной и самостоятельных работ, тестирования, практических работ, дифференцированного зачета, а также при проверке индивидуальных заданий обучающихся, предназначенных для внеаудиторной самостоятельной работы.
| Результаты обучения (личностные, предметные, метапредметные) | Формы и методы контроля и оценки результатов обучения |
| личностные результаты: 1)воспитание гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада учёных Донбасса в развитие мировой науки; 2) формирование мировоззрения, соответствующего современному уровню развития науки и общественной практики; 3) ответственное отношение к обучению, готовность и способность к саморазвитию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности; 4) осознанный выбор будущей профессиональной деятельности на базе ориентирования в мире профессий и профессиональных предпочтений; отношение к профессиональной деятельности как к возможности участия в решении личных, общественных, государственных и общенациональных проблем; формирование уважительного отношения к труду; развитие опыта участия в социально значимом труде; 5) умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности; 6) умение управлять своей познавательной деятельностью; 7) умение взаимодействовать с одноклассниками, детьми младшего возраста и взрослыми в образовательной, общественно-полезной, учебно-исследовательской, проектной и других видах деятельности; 8) критичность мышления, инициатива, находчивость, активность при решении математических задач. метапредметные результаты: 1) умение самостоятельно определять цели своей деятельности, ставить и формулировать для себя новые задачи в учёбе; 2) умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией; 3) умение самостоятельно принимать решения, проводить анализ своей деятельности, применять различные методы познания; 4) владение навыками познавательной, учебно-исследовательской и проектной деятельности; 5) формирование понятийного аппарата, умения создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации; 6) умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы; 7) формирование компетентности в области использования информационно-коммуникационных технологий; 8) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни; 9) умение самостоятельно осуществлять поиск в различных источниках, отбор, анализ, систематизацию и классификацию информации, необходимой для решения математических проблем, представлять её в понятной форме; принимать решение в условиях неполной или избыточной, точной или вероятностной информации; критически оценивать и интерпретировать информацию, получаемую из различных источников; 10) умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки; 11) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; 12) умение использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации. предметные результаты: 1) осознание значения математики для повседневной жизни человека; 2) представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации; 3) умение описывать явления реального мира на математическом языке; представление о математических понятиях и математических моделях как о важнейшем инструментарии, позволяющем описывать и изучать разные процессы и явления; 4) представление об основных понятиях, идеях и методах геометрии; 5) владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач; 6) практически значимые математические умения и навыки, способность их применения к решению математических и нематематических задач. 7) владение навыками использования компьютерных программ при решении математических задач; 8) практически значимые математические умения и навыки, способность их применения к решению математических и нематематических задач, предполагающие умения: - выполнять вычисления с действительными числами; - решать рациональные, иррациональные, показательные, логарифмические, степенные и тригонометрические уравнения, системы уравнений; - решать рациональные, иррациональные, показательные, логарифмические, степенные и тригонометрические неравенства, системы неравенств; - решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений, систем уравнений и неравенств; - использовать алгебраический «язык» для описания предметов окружающего мира и создания соответствующих математических моделей; - выполнять тождественные преобразования рациональных, иррациональных, показательных, логарифмических, степенных, тригонометрических выражений; - выполнять операции над множествами; - исследовать функции с помощью производной и строить их графики; - вычислять площади фигур и объёмы тел с помощью определённого интеграла; - проводить вычисление статистических характеристик, выполнять приближённые вычисления; - решать комбинаторные и вероятностные задачи. | письменные и устные опросы обучающихся; аудиторные самостоятельные работы; тестирование; учебные задания для решения практических задач; домашние индивидуальные задания по решению задач профессиональной направленности; подготовка докладов, рефератов; экзамен
|
11















