Пояснительная записка
Рабочая программа курса алгебры 9 класса составлена в соответствии с требованиями Федерального государственного образовательного стандарта второго поколения основного общего образования, соответствует положениям Федерального государственного образовательного стандарта основного общего образования, в том числе требованиям к результатам освоения основной образовательной программы, фундаментальному ядру содержания общего образования, Примерной программе по математике. Программа отражает идеи и положения Концепции духовно-нравственного развития и воспитания личности гражданина России, Программы формирования универсальных учебных действий (УУД), составляющих основу для саморазвития и непрерывного образования, выработки коммуникативных качеств, целостности общекультурного, личностного и познавательного развития учащихся. Программы общеобразовательных учреждений. Алгебра. 7-9 классы. / Сост. Бурмистрова Т.А. – М. «Просвещение», 2014 г. Авторская программа по алгебре Ю.Н. Макарычев, Н.Г. Миндюк и др.
Рабочая программа по алгебре составлена с использованием нормативно-правовой базы:
1. Закона 273 – ФЗ «Об образовании в Российской Федерации» от 29 декабря 2012 года.
2. На основании приказа Министерства образования и науки Российской Федерации от 31 декабря 2015 года № 1577 «О внесении изменений в федеральный государственный образовательный стандарт основного общего образования, утверждённый приказом Министерства образования и науки Российской Федерации» от 17 декабря 2010 года № 1897.
3. На основании разработанного Положения «О структуре, порядке разработки и утверждения рабочих программ учебных курсов, предметов, дисциплин (модулей) в общеобразовательном учреждении реализующая программы общего образования, утвержденного приказом директора.
Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы. Обучение математике направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Задачи:
Развитие:
Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей; математической речи; двигательной моторики; внимания; памяти; навыков само и взаимопроверки.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
Культуры личности, отношения к математике как к части общечеловеческой культуры, волевых качеств; коммуникабельности; ответственности.
Предлагаемая учебная программа позволяет обеспечить формирование, как предметных умений, так и универсальных учебных действий школьников, а также способствует достижению определённых во ФГОС личностных результатов, которые в дальнейшем позволят учащимся применять полученные знания и умения для решения различных жизненных задач.
Рабочая программа опирается на УМК:
- Алгебра: учебник для 9 класса общеобразовательных учреждений. Составители:.Макарычев Ю. Н. и др., 2015.
- Дидактические материалы по алгебре.9 класс. / Ю.Н. Макарычев, Н.Г. Миндюк, Л.М. Короткова. / М: Просвещение, 2015
Согласно Федеральному базисному учебному плану для образовательных организаций Российской Федерации для обязательного изучения математики на этапе основного общего образования отводится не менее 136 часов из расчета 4 часа в неделю. Количество контрольных работ – 8 (в том числе итоговая контрольная работа).
2. Планируемые результаты освоения учебного предмета
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
личностные:
сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими, в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
метапредметные:
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родо-видовых связей;
умение устанавливать причинно-следственные связи; строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаковосимволические средства, модели и схемы для решения учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ- компетентности);
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
Предметными результатами изучения алгебры в 9 классе являются следующие умения:
1.Квадратичная функция:
строить график квадратичной функции и применять графические представления для решения неравенств второй степени с одной переменной; выполнять простейшие преобразования графиков функций;
находить область определения и область значений функции, промежутки знакопостоянства, промежутки возрастания и убывания функций, наибольшее и наименьшее значения, точки пересечения графика квадратичной функции с осями координат, нули функции;
находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; решать квадратные уравнения, определять знаки корней; выполнять разложение квадратного трехчлена на множители; решать квадратное неравенство методом интервалов.
2.Уравнения и неравенства с одной переменной:
решать целые уравнения методом введения новой переменной; разложением на множители и графическим способом;
решать системы двух уравнений с двумя переменными графическим способом.
3.Уравнения и неравенства с двумя переменными:
решать уравнения с двумя переменными способом подстановки и сложения;
решать задачи на совместную работу, на движение и другие составлением систем уравнений.
4.Прогрессии:
понимать значения терминов «член последовательности», «номер члена последовательности»;
находить разность арифметической прогрессии, сумму n первых членов арифметической прогрессии и любой член арифметической прогрессии;
вычислять любой член геометрической прогрессии по формуле, знать свойства членов геометрической прогрессии, находить сумму n первых членов геометрической прогрессии;
выявлять, какая последовательность является арифметической (геометрической), если да, то находить d (q);
5.Степень с рациональным показателем:
строить график функции у = хn, знать свойства степенной функции с натуральным показателем, уметь решать уравнения хn = а при четных и нечетных значениях n;
выполнять простейшие преобразования и вычисления выражений, содержащих корни, применяя определение и изученные свойства арифметического корня n-й степени;
выполнять простейшие преобразования выражений, содержащих степени с дробным показателем, используя при этом изученные свойства степеней с рациональным показателем.
3. Содержание изучаемого предмета
Повторение (10 ч)
Глава 1. Свойства функций. Квадратичная функция (26 ч)
Функция. Свойства функций. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция у = ах2 + bх + с, её свойства и график. Неравенства второй степени с одной переменной. Метод интервалов. Четная и нечетная функция. Функция у = хn. Определение корня n-й степени. Вычисление корней n -й степени.
Цель: расширить сведения о свойствах функций, ознакомить обучающихся со свойствами и графиком квадратичной функции, сформировать умение решать неравенства вида ах2 + bх + с0 ах2 + bх + с где а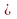 0. Ввести понятие корня n -й степени.
0. Ввести понятие корня n -й степени.
В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область определения функции, график. Даются понятия о возрастании и убывании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.
Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квадратного трехчлена, разложении квадратного трехчлена на множители.
Изучение квадратичной функции начинается с рассмотрения функции у=ах2, её свойств и особенностей графика, а также других частных видов квадратичной функции – функции у=ах2+n, у=а(х-m)2. Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции у = ах2 + bх + с может быть получен из графика функции у = ах2 с помощью двух параллельных переносов. Приёмы построения графика функции у = ах2 + bх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.
При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак.
Формирование умений решать неравенства вида ах2 + bх + с0 ах2 + bх + с где а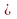 0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей параболы ее расположение относительно оси Ох).
0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей параболы ее расположение относительно оси Ох).
Обучающиеся знакомятся с методом интервалов, с помощью которого решаются несложные рациональные неравенства.
Обучающиеся знакомятся со свойствами степенной функции у=хn при четном и нечетном натуральном показателе n.. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида 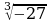 ,
, 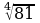 . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
. Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
Глава 2. Уравнения и неравенства с одной переменной (24 ч)
Целые уравнения. Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени.
Цель: систематизировать и обобщить сведения о решении целых с одной переменной, Выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем; выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем.
В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях. Вводятся понятия целого рационального уравнения и его степени. Обучающиеся знакомятся с решением уравнений третьей степени и четвертой степени с помощью разложения на множители и введения вспомогательной переменной. Метод решения уравнений путем введения вспомогательных переменных будет широко использоваться дальнейшем при решении тригонометрических, логарифмических и других видов уравнений.
В данной теме завершаемся изучение систем уравнений с двумя. переменными. Основное внимание уделяется системам, в которых одно из уравнений первой степени, а другое второй. Известный обучающимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к решению квадратного уравнения.
Ознакомление обучающихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени, должно осуществляться с достаточной осторожностью и ограничиваться простейшими примерами.
Привлечение известных обучающимся графиков позволяет привести примеры графического решения систем уравнений. С помощью графических представлений можно наглядно показать обучающимся, что системы двух уравнений с двумя переменными второй степени могут иметь одно, два, три, четыре решения или не иметь решений.
Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач, решаемых с помощью систем уравнений.
Глава 3. Уравнения и неравенства с двумя переменными ( 28ч)
Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы.
Цель — выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем.
В данной теме завершается изучение систем уравнений с двумя переменными. Основное внимание уделяется системам, в которых одно из уравнений первой степени, а другое второй. Известный учащимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к решению квадратного уравнения. Учащиеся должны уметь решать системы двух уравнений с двумя переменными, указанные в содержании. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления системы уравнений; решать составленную систему уравнений; интерпретировать результат. Решать системы неравенств с двумя переменными.
Глава 4. Прогрессии (25ч)
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия.
Цель: дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.
При изучении темы вводится понятие последовательности, разъясняется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий.
Работа с формулами n-го члена и суммы первых n членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем.
Рассматриваются характеристические свойства арифметической и геометрической прогрессий, что позволяет расширить круг предлагаемых задач.
Глава 5. Повторение(23 ч)
Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры основной общеобразовательной школы.
4. Тематическое планирование
| Номер | Содержание материала | Количество часов | Виды контроля |
| 1.
| Повторение
| 10 | с/р, к/р |
| 2. | Свойства функций. Квадратичная функция | 26 | с/р, к/р |
| 3. | Уравнения и неравенства с одной переменной. | 24 | с/р, к/р |
| 4. | Уравнения и неравенства с двумя переменными. | 28 | с/р, к/р |
| 5. | Арифметическая и геометрическая прогрессии | 25 | с/р, к/р |
| 6. | Итоговое повторение | 23 | с/р, к/р |
5. Литература
Алгебра, учебник для 9 класса для общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б. Суворова : Просвещение, 2016.
Алгебра: элементы статистики и теории вероятностей. Учебное пособие для учащихся 7 – 9 классов общеобразовательных учреждений / / Ю.Н. Макарычев, Н.Г. Миндюк: Просвещение, 2015.
Дидактические материалы по алгебре для 9 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк: Просвещение 2015.
Сборника рабочих программ по алгебре. 7 – 9 классы», - М.: Просвещение, 2014. Составитель Т.А. Бурмистрова
«Алгебра. Контрольные работы 7-9» - М. Просвещение, 2008. Авторы: Л. В. Кузнецова, С.С. Минаев, Л. О. Рослова
Сборник тестовых заданий для тематического и обобщающего контроля» -. Интеллект-Центр 2017, автор Крайнева Л. Б.
«Тесты для промежуточной аттестации» -Легион. Ростов-на-Дону 2019 под редакцией Ф. Ф. Лысенко.
«Алгебра. Разноуровневые контрольные тесты 9 класс» Н. В. Барышникова, издательство «Учитель» Волгоград 2018.г.
«Алгебра. Проверочные работы с элементами тестирования» Воробьева Е. А. издательство «Лицей» 2018.г.
Календарно-тематическое планирование
| № п/п | Содержание учебного материала | Кол-во часов | Виды контроля | Дата проведения |
| План | Фактич |
| | Повторение | 10 |
|
|
|
| 1-2 | Рациональные дроби и их свойства | 2 |
|
|
|
| 3-4 | Преобразование рациональных выражений. | 2 | с/р |
|
|
| 5 | Построение графиков функций. | 1 |
|
|
|
| 6 | Неравенства. Системы неравенств | 1 | с/р |
|
|
| 7 | Решение задач на составление рациональных уравнений | 1 |
|
|
|
| 8 | Решение уравнений | 1 | с/р |
|
|
| 9 | Степень с целым показателем | 1 | с/р |
|
|
| 10 | Входная контрольная работа | 1 | к/р |
|
|
|
| 1. Свойства функций. Квадратичная функция | 26 |
|
|
|
| 11-13 | Функция. Область определения и область значений функции | 3 |
|
|
|
| 14-15 | Свойства функций | 2 |
|
|
|
| 16-17 | Квадратный трехчлен и его корни | 2 |
|
|
|
| 18-20 | Разложение квадратного трехчлена на множители | 3 | с/р |
|
|
| 21-23 | Функция y=ax2 , ее график и свойства | 3 |
|
|
|
| 24-27 | Графики функций y=ax2+n и y=a(x-m)2 | 4 | с/р |
|
|
| 28-30 | Построение графика квадратичной функции | 3 | с/р |
|
|
| 31-32 | Функция y=xn | 2 |
|
|
|
| 33-34 | Корень n-ой степени. | 2 | с/р |
|
|
| 35 | Контрольная работа № 1 "Квадратичная функция" | 1 | к/р |
|
|
| 36 | Анализ контрольной работы | 1 |
|
|
|
|
| Глава II. Уравнения и неравенства с одной переменной. | 24 |
|
|
|
| 37-40 | Целое уравнение и его корни | 4 |
|
|
|
| 41-46 | Дробные рациональные уравнения | 6 | с/р |
|
|
| 47-52 | Решение неравенств второй степени с одной переменной | 6 | с/р |
|
|
| 53-58 | Решение неравенств методом интервалов | 6 |
|
|
|
| 59 | Контрольная работа № 2 по теме "Уравнения и неравенства с одной переменной | 1 | к/р |
|
|
| 60 | Анализ контрольной работы | 1 |
|
|
|
|
| Глава III. Уравнения и неравенства с двумя переменными. | 28 |
|
|
|
| 61-64 | Уравнение с двумя переменными и его график | 4 | с/р |
|
|
| 65-68 | Графический способ решения систем уравнений | 4 | с/р |
|
|
| 69-72 | Решение систем второй степени | 4 | с/р |
|
|
| 73-77 | Решение задач с помощью систем уравнений второй степени | 5 | с/р |
|
|
| 78-81 | Неравенства с двумя переменными | 4 | с/р |
|
|
| 82-86 | Системы неравенств с двумя переменными | 5 | с/р |
|
|
| 87 | Контрольная работа № 3 "Решение систем уравнений и неравенств" | 1 | к/р |
|
|
| 88 | Анализ контрольной работы. | 1 |
|
|
|
|
| Глава IV. Арифметическая и геометрическая прогрессии | 25 |
|
|
|
| 89-90 | Последовательности | 2 |
|
|
|
| 91-94 | Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии | 4 | с/р |
|
|
| 95-99 | Формула суммы n первых членов арифметической прогрессии | 5 | с/р |
|
|
| 100 | Контрольная работа № 4 по теме "Арифметическая прогрессия" | 1 | к/р |
|
|
| 101 | Анализ контрольной работы. | 1 |
|
|
|
| 102-106 | Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии | 5 | с/р |
|
|
| 107-111 | Формула суммы n первых членов геометрической прогрессии | 5 | с/р |
|
|
| 112 | Контрольная работа № 5 по теме "Геометрическая прогрессия" | 1 | к/р |
|
|
| 113 | Анализ контрольной работы. | 1 |
|
|
|
|
| Итоговое повторение | 23 |
|
|
|
| 114 | Алгебраические выражения | 1 |
|
|
|
| 115-117 | Алгебраические выражения | 3 | с/р |
|
|
| 118-119 | Уравнения | 2 | с/р |
|
|
| 120 | Системы уравнений | 1 |
|
|
|
| 121-123 | Системы уравнений | 3 | с/р |
|
|
| 124 | Текстовые задачи | 1 |
|
|
|
| 125-127 | Текстовые задачи | 3 | с/р |
|
|
| 128-129 | Неравенства | 2 | с/р |
|
|
| 130 | Функции и графики | 1 |
|
|
|
| 131-133 | Функции и графики | 3 | с/р |
|
|
| 134-135 | Итоговая контрольная работа | 2 | к/р |
|
|
| 136 | Итоговый урок | 1 |
|
|
|







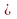 0. Ввести понятие корня n -й степени.
0. Ввести понятие корня n -й степени.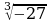 ,
, 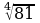 . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
. Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.









