МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
« ШКОЛА № 5»
| Рассмотрено на заседании ЭМС Протокол №2 «26»08.2014 г Председатель ЭМС зам.директора по НМР _____________А.Г.Миносьянц
| СОГЛАСОВАНО: «28»08.2014г Зам.директора по УВР. ___________С.Е.Каминская | УТВЕРЖДАЮ: «30» 08.2014г Директор МБОУ «Школа №5 __________Курбанова Т.В. |
РАБОЧАЯ ПРОГРАММА УЧЕБНОГО ПРЕДМЕТА
«АЛГЕБРА»
для обучающихся 7 классе ФГОС
|
|
Разработчики рабочей программы учебного предмета «АЛГЕБРА»: Салатова Ирина Николаевна, учитель математики высшей квалификационной категории Гончарова С.В. учитель математики первой квалификационной категории |
г. Муравленко, 2014
Пояснительная записка
Рабочая программа основного общего образования составлена на основе:
-
Федерального закона РФ от 29.12.2012 № 273-ФЗ "Об образовании в Российской Федерации";
-
Образовательной программы «Отличная школа» МБОУ СОШ № 5» » Утверждена Приказом директора школы №567 от 30.08.2014 г.
-
Положением МБОУ СОШ № 5 «О рабочей программе по учебному предмету в рамках реализации ФГОС второго поколения» № 450 от 19.09.2013 г.
-
Примерная программа основного общего образования по математике. Программы общеобразовательных учреждений. Алгебра. 7-9 классы. «Просвещение», 2010 г. Составитель Т.А.Бурмистрова.
Данная учебная программа ориентирована на учащихся 7 класса
Новая парадигма образования, реализуемая ФГОС, – это переход от школы информационно-трансляционной к школе деятельностной, формирующей у обучающихся универсальные учебные действия, необходимые для решения конкретных личностно значимых задач.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Структура рабочей программы
Рабочая программа включает в себя 5 разделов:
1.Пояснительная записка.
2.Общая характеристика учебного предмета.
3.Описание места учебного предмета курса в учебном плане Личностные, метапредметные и предметные результаты освоения конкретного учебного предмета, курса (для ООО).
4. Содержание тем учебного курса.
5. Описание учебно-методическое и материально-технического обеспечения образовательного процесса.
Программа модифицирована. Внесение изменения в рабочую программу составляют 15 %. За счет перераспределения времени выделении резерв в каждом полугодии для реализации выполнения программы в условиях Крайнего Севера, из – за необходимости коррекции знаний учащихся. Данная программа содержит все темы, включенные в федеральный компонент содержания образования. Наряду с федеральным компонентом программы реализуется региональный компонент, который представлен следующими темами «Статистические характеристики», « Решение задач с помощью систем уравнений».
Изучение алгебры направлено на реализацию целей и задач, сформулированных в Федеральном государственном стандарте общего образования по математике:
- овладение системой математических знаний и умений, необходимых для применения в практической деятельности, продолжения образования;
- интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе;
- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры.
В ходе освоения содержания курса учащиеся получают возможность:
-
сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
-
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
-
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
-
развить логическое мышление и речь — умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
-
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В ходе преподавания алгебры в 7 классах, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
-
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
-
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
-
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
-
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
-
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
-
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Срок реализации рабочей программы – 1 год.
Система оценки достижений учащихся заключается:
-
Оценка письменных контрольных работ обучающихся по математике.
-
Ответ оценивается отметкой «5», если:
-
работа выполнена полностью;
-
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
-
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
-
Отметка «4» ставится в следующих случаях:
-
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
-
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
-
Отметка «3» ставится, если:
-
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
-
Отметка «2» ставится, если:
-
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
2. Оценка устных ответов обучающихся по математике
-
Ответ оценивается отметкой «5», если ученик:
-
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
-
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
-
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
-
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
-
отвечал самостоятельно, без наводящих вопросов учителя;
-
возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
-
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
-
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
-
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
-
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
-
Отметка «3» ставится в следующих случаях:
-
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
-
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
-
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
-
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
-
Отметка «2» ставится в следующих случаях:
-
не раскрыто основное содержание учебного материала;
-
обнаружено незнание учеником большей или наиболее важной части учебного материала;
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
3. Общая классификация ошибок.
3.1. Грубыми считаются ошибки:
-
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
-
незнание наименований единиц измерения;
-
неумение выделить в ответе главное;
-
неумение применять знания, алгоритмы для решения задач;
-
неумение делать выводы и обобщения;
-
неумение читать и строить графики;
-
неумение пользоваться первоисточниками, учебником и справочниками;
-
потеря корня или сохранение постороннего корня;
-
отбрасывание без объяснений одного из них;
-
равнозначные им ошибки;
-
вычислительные ошибки, если они не являются опиской;
-
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
-
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
-
неточность графика;
-
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
-
нерациональные методы работы со справочной и другой литературой;
-
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
-
нерациональные приемы вычислений и преобразований;
-
небрежное выполнение записей, чертежей, схем, графиков.
Основным инструментарием для оценивания результатов является:
Устный опрос – устная форма контроля знаний и умений, используется взаимопроверка, самопроверка по образцу, заслушивание ответа и его оценивание учителем.
Математический диктант – письменная форма контроля, применяемая для проверки умения правильно понимать и записывать числа, математические термины и понятия.
Самостоятельная работа – письменная форма контроля, рассчитанная на 5 – 20 мин, применяется для оценивания уровня сформированности знаний и умений по изучаемому вопросу в теме.
Практическая работа – форма контроля, применяется для оценивания умения выполнять определенные практические действия, применяя знания математики.
Контрольная работа – письменная форма контроля знаний, умений и навыков по изучаемой теме, рассчитана на выполнение в течение урока.
Контрольно-измерительные материалы (тесты)
Общая характеристика учебного предмета
Данная программа составлена на основе примерной программы общеобразовательных учреждений. Алгебра. 7-9 классы. «Просвещение», 2011 г. Составитель Т.А.Бурмистрова с учётом требований федерального компонента государственного стандарта общего образования и в соответствии с авторской программой Ю.Н. Макарычева.
Цели обучения алгебре в 7 классах определены следующим образом:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношение к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
В ходе обучения алгебре по данной программе с использованием учебника и методического пособия для учителя, решаются следующие задачи:
-
развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.);
-
усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач;
-
осуществление функциональной подготовки учащихся;
-
овладение конкретными знаниями необходимыми для применения в практической деятельности;
выявление и развитие математических способностей, интеллектуального развития ученика.
В курсе алгебры можно выделить следующие основные содержательные линии: арифметика; алгебра; функции.
Содержание линии «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами. А также приобретению практических навыков, необходимых в повседневной жизни.
Содержание линии «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разделов математики, смежных предметов и окружающей реальности.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики.
Описание места учебного предмета курса в учебном плане
Образовательная область – математика.
Согласно федеральному базисному учебному плану на изучение алгебры в 7 классе отводится не менее 136 часов из расчета 4 ч в неделю. Преподавание ведется по первому варианту в 7 классе – 3 часа в неделю, всего 105 часов.
Личностные, метапредметные и предметные результаты освоения конкретного учебного предмета, курса (для ООО)
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования
Личностные:
-
сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию и саморазвитию на основе мотивации к обучению и познанию;
-
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
-
сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими, в образовательной, общественно полезной учебно – исследовательской, творческой и других видах деятельности;
-
представление о математической науке как сфере человеческой деятельности, об этапах ее развития цивилизации;
-
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
-
креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
-
умение контролировать процесс и результат учебной математической деятельности.
Метапредметные:
-
умение самостоятельно планировать альтернативные пути достижений целей, осознано выбирать наиболее эффективные способы решения учебных и познавательных задач;
-
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
-
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;
-
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий классификация на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
-
сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий
Предметные :
-
умение работать с математическим текстом (структурирование, извлечение необходимой информации ),точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики;
-
владение базовым понятийным аппаратом;
-
умение выполнять алгебраические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
-
умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
-
умение решать линейные и квадратные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы; применять графические представления для решения и исследования уравнений, неравенств, систем; применять полученные умения для решения задач из математики, смежных предметов, практики;
-
овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально – графические представления для описания и анализа математических задач и реальных зависимостей.
Формирование УУД
| Метапреметные | Исследовательская деятельность. Смысловое чтение: оценка информации |
| Личностные | Мотивация к познанию через анализ и нравственно-этическую оценку |
| Коммуникативные | Организация и осуществление сотрудничества: ретрансляция опыта, взаимообучение, ролевые игры. |
| Познавательные | Эмпирические исследования |
| Регулятивные | Коррекция деятельности: рефлексия, оценивание, самоконтроль |
Содержание тем учебного курса
| № | Тема | Кол-во часов в прим. програм. | Кол-во часов в раб. програм | Контрольных работ |
| 1 | Повторение курса математики 6 класса | - | 2 |
|
| 2 | Выражения, тождества, уравнения. | 22 | 21 | 2 |
| 3 | Функции. | 11 | 13 | 1 |
| 4 | Степень с натуральным показателем. | 11 | 13 | 1 |
| 5 | Многочлены. | 17 | 17 | 2 |
| 6 | Формулы сокращённого умножения. | 19 | 20 | 2 |
| 7 | Системы линейных уравнений. | 16 | 15 | 1 |
| 8 | Повторение. Решение задач по курсу алгебры 7 | 6+3 итог.контр.+ 1 зач. | 6 | 1 |
|
| Итого | 105 | 105ч | 10 |
1. Повторение (2 часа)
Основная цель: Актуализация опорных знаний умений и навыков сформированных в 6 классе.
2. Выражения, тождества, уравнения (21 час).
Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений.
Основная цель – систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.
Первая тема курса 7 класса является связующими звеном между курсом математики 5-6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.
Нахождение значений числовых и буквенных выражений дает возможность повторить с учащимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.
В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки 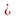 и
и 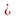 , дается понятие о двойных неравенствах.
, дается понятие о двойных неравенствах.
При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.
Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия учащимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах=b при различных значениях а и b. Продолжается работа по формированию у учащихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе.
3.Функции (13 часов).
Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и ее график.
Основная цель – ознакомить учащихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида.
Данная тема является начальным этапом в систематической функциональной подготовке учащихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у учащихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же работу по графику и решать по графику обратную задачу.
Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида – прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у=kx, где k≠0, как зависит от значений k и b взаимное расположение графиков двух функций вида у=kx+b.
Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.
4. Степень с натуральным показателем (13 часов).
Степень с натуральным показателем и ее свойства. Одночлен. Функции у = х2, у = х3 и их графики.
Основная цель: - выработать умение выполнять действия над основными степенями с натуральными показателями.
В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора. Рассматриваются свойства степени с натуральным показателем. На примере доказательства свойств ат • ап = ат + п, ат : ап = ат~ п, где т л, (ат)п = атп, (ab)n = апbп учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений, содержащих степени, особое внимание следует обратить на порядок действий.
Рассмотрение функций у = х2, у = х3 позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание учащихся на особенности графика функции у = х2: график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.
Умение строить графики функций у = х2 и у = х3 используется для ознакомления учащихся с графическим способом решения уравнений.
5. Многочлены (17 часов).
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.
Основная цель — выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.
Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами — сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.
Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.
В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.
6. Формулы сокращенного умножения (20 часов).
Формулы (а ± b)2 = а2± 2аb + b2, (а ± b)3 = а3 ± 3а2b + 3ab2 ± b3, (а ± b) (а2 + ab + b2) = а3 ± b3. Применение формул сокращенного умножения в преобразованиях выражений.
Основная цель — выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.
В данной теме продолжается работа по формированию у учащихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b) (а + b) = а2 - b2, (а ± b)2 = а2 ± 2аb + b2. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево».
Наряду с указанными рассматриваются также формулы (а ± b)3 = а3± 3а2b + Заb2 ± b3, а3±b3 = (а± b) (а2 + аb + b2). Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.
В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач.
7. Системы линейных уравнений (15 часов).
Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.
Основная цель — ознакомить учащихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.
Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений.
Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.
Формируется умение строить график уравнения а + by = с, где а ≠ 0 или b≠0, при различных значениях а, b, с. Введение графических образов дает возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными.
Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задачи с обычного языка на язык уравнений.
8. Повторение (6 часов).
Литература для учителя
-
Макарычев Ю.Н., Миндюк Н.Г., Пешков К.И., Суворова С.В.А.В «Алгебра 7 класс»,. - М.: Просвещение, 2013.
-
Алгебра. Тесты для промежуточной аттестации. 7-8 класс. Издание второе, переработанное. Под редакцией Ф.Ф. Лысенко. Ростов-на-Дону: Легион, 2009. – 160 с.
-
Государственный стандарт основного общего образования по математике.
-
Дидактические материалы по алгебре для 7 класса – 5-е изд., перераб. Гусев В.А., Медяник А.И. – М.: Просвещение, 2009-2014.
-
Задачи повышенной трудности в курсе алгебры 7-9 классов: Книга для учителя. Н.П. Кострикина. – М.: Просвещение, 1991.
-
История математики в школе. VII-VIII кл. Пособие для учителей. / Г.И. Глейзер – М.: Просвещение, 1982 – 240 с.
-
Контрольные и самостоятельные работы по алгебре: 7 класс: к учебнику Макарычева Ю.Н.и др. "Алгебра. Геометрия 7 класс" /А.П.Ершова. – 2-е изд., стереотип. – М.: Издательство «Илекса», 2008. – 158 с.
-
Программы. Математика7-9классы / авт.-сост..Бурмистрова Т.А. – М.: Просвещение, 2009.
-
Поурочные разработки по алгебре к учебнику Ю.Н. Макарычева «Алгебра7 класс»/ А.Н. Рурукин, Г.В.Лупенко, И.А. Масленникова. – М. «ВАКО» 2009 г.
Литература для учащихся
-
Макарычев Ю.Н., Миндюк Н.Г., Пешков К.И., Суворова С.В.А.В «Алгебра7 класс »,. - М.: Просвещение, 2013
-
Дидактические материалы по алгебре для 7 класса – 5-е изд., перераб. Гусев В.А., Медяник А.И. – М.: Просвещение, 2009-2014.
-
История математики в школе. VII-VIII кл. Пособие для учителей. / Г.И. Глейзер – М.: Просвещение, 1982 – 240 с.
Технические средства обучения
Компьютер, медиапроектор, экран
Интернет-ресурсы
1. www. edu - "Российское образование" Федеральный портал.
2. www.school.edu - "Российский общеобразовательный портал".
3. www.school-collection.edu.ru/ Единая коллекция цифровых образовательных ресурсов
4. www.mathvaz.ru - docье школьного учителя математики
Документация, рабочие материалы для учителя математики
5. www.it-n.ru"Сеть творческих учителей"
6. www .festival.1september.ru Фестиваль педагогических идей "Открытый урок"
Приложение.
Контрольная работа по теме «Преобразование выражений»
Вариант 1
• 1. Найдите значение выражения 6x - 8y, при x = 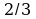 , у =
, у = 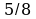 .
.
• 2. Сравните значения выражений -0,8x - 1 и 0,8x - 1 при x = 6.
• 3. Упростите выражение:
а) 2x - Зy - 11х + 8у; б) 5(2а + 1) - 3; в) 14x - (x - 1) + (2х + 6).
4. Упростите выражение и найдите его значение:
-4 (2,5а - 1,5) + 5,5а – 8, при а = - 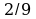 .
.
5. Из двух городов, расстояние между которыми s км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через t ч. Скорость легкового автомобиля v км/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, еcли s = 200, t = 2, v = 60.
6. Раскройте скобки: Зx - (5x - (3x - 1)).
Контрольная работа по теме «Преобразование выражений»
Вариант 2
• 1. Найдите значение выражения 16а + 2y, при а = 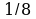 , у = -
, у = - 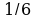 .
.
• 2. Сравните значения выражений 2 + 0,3а и 2 - 0,3а, при а = - 9.
• 3. Упростите выражение:
а) 5а + 7b - 2а - 8b; б) 3 (4x + 2) - 5; в) 20b - (b - 3) + (Зb - 10).
4. Упростите выражение и найдите его значение:
-6 (0,5x - 1,5) - 4,5x – 8, при x = 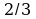 .
.
5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через t ч. Найдите расстояние между городами, если скорость автомобиля v1 км/ч, а скорость мотоцикла v2 км/ч. Ответьте на вопрос задачи, если: t = 3, v1 = 80, v2 = 60.
6. Раскройте скобки: 2р - (3р - (2р - с)).
Контрольная работа «Уравнения с одной переменной»
Вариант 1
• 1. Решите уравнение:
| а) 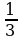 x = 12; x = 12; б) 6x - 10,2 = 0; | в) 5x - 4,5 = 3x + 2,5; г) 2x - (6x - 5) = 45. |
• 2. Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у нее занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
3. В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в двух сараях первоначально?
4. Решите уравнение 7х - (х + 3) = 3 (2х - 1).
Контрольная работа «Уравнения с одной переменной»
Вариант 2
• 1. Решите уравнение:
| а) 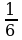 х = 18; х = 18; б) 7x + 11,9 = 0; | в) 6х - 0,8 = 3х + 2,2; г) 5х - (7х + 7) = 9. |
• 2. Часть пути в 600 км турист пролетел на самолете, а часть проехал на автобусе. На самолете он проделал путь, в 9 раз больший, чем на автобусе. Сколько километров турист проехал на автобусе?
3. На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на второй посадили еще 90, на обоих участках саженцев стало поровну. Сколько всего саженцев было на двух участках первоначально?
4. Решите уравнение 6х - (2х - 5) = 2 (2х + 4).
Контрольная работа по теме «Линейная функция»
Вариант 1
• 1. Функция задана формулой у = 6х + 19. Определите: а) значение у, если х = 0,5; б) значение х, при котором у = 1; в) проходит ли график функции через точку А (-2; 7).
• 2. а) Постройте график функции у = 2х - 4.
б) Укажите с помощью графика, чему равно значение у, при х = 1,5.
• 3. В одной и той же системе координат постройте графики функций: а) у = -2х; б) у = 3.
4. Найдите координаты точки пересечения графиков функций у= 47х - 37 и у = -13х + 23.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х - 7 и проходит через начало координат.
Контрольная работа по теме «Линейная функция»
Вариант 2
• 1. Функция задана формулой у = 4х - 30. Определите:
а) значение у, если х = -2,5; б) значение х, при котором у = -6; в) проходит ли график функции через точку В (7; -3).
• 2. а) Постройте график функции у = -3х + 3.
б) Укажите с помощью графика, при каком значении х значение у равно 6.
• 3. В одной и той же системе координат постройте графики функций: а) у = 0,5х; б) у = -4.
4. Найдите координаты точки пересечения графиков функций у= -38х + 15 и у = -21х - 36.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = -5х + 8 и проходит через начало координат.
Контрольная работа по теме «Степень с натуральным показателем»
Вариант 1
• 1. Найдите значение выражения 1 - 5х2, при х = -4.
• 2. Выполните действия:
а) y7 • y12; б) y20 : y5; в) (y2)8; г) (2у)4.
• 3. Упростите выражение: а) -2аb3 • 3а2 • b4; б) (- 2а5b2)3.
• 4. Постройте график функции у = х2. С помощью графика определите значение у при х = 1,5; х = -1,5.
5. Вычислите: 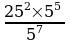 .
.
6. Упростите выражение: a) 2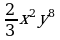 •
•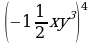 ; б) xn – 2 • x3 – n • x.
; б) xn – 2 • x3 – n • x.
Контрольная работа по теме «Степень с натуральным показателем»
Вариант 2
• 1. Найдите значение выражения -9р3, при р = - 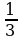 .
.
• 2. Выполните действия: а) с3 • с22; б) с18 : с6; в) (с4)6; г) (3с)5.
• 3. Упростите выражение: а) -4х5у2 • Зху4; б) (Зх2y3)2.
• 4. Постройте график функции у = х2. С помощью графика функции определите, при каких значениях х значение y равно 4.
5. Вычислите: 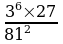 .
.
6. Упростите выражение: a) 3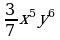 •
•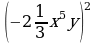 ; б) (an + 1 )2 : a 2n.
; б) (an + 1 )2 : a 2n.
Контрольная работа по теме «Сумма, разность многочленов»
Вариант 1
• 1. Выполните действия: а) (За - 4ах + 2) - (11а - 14ах); б) 3у2 (у3 + 1).
• 2. Вынесите общий множитель за скобки: а) 10аb - 15b2; б) 18а3 + 6а2.
• 3. Решите уравнение 9х - 6 (х - 1) = 5 (х + 2).
• 4. Пассажирский поезд за 4 ч прошел такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше.
5. Решите уравнение 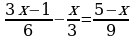 .
.
6. Упростите выражение 2а (а + b - с) – 2b (а - b - с) + 2с (а - b + с).
Контрольная работа по теме «Сумма, разность многочленов»
Вариант 2
• 1. Выполните действия: а) (2а2 - За + 1) - (7а2 - 5а); б) 3х (4х2 - х).
• 2. Вынесите общий множитель за скобки: а) 2ху - 3ху2; б) 8b4 + 2b3.
• 3. Решите уравнение 7 - 4 (3х - 1) = 5 (1 - 2х).
• 4. В трех шестых классах 91 ученик. В 6 «А» на 2 ученика меньше, чем в 6 «Б», а в 6 «В» на 3 ученика больше, чем в 6 «Б». Сколько учащихся в каждом классе?
5. Решите уравнение 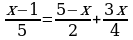 .
.
6. Упростите выражение 3х (х + у + с) - 3у (х - у - с) - 3с (х + у - с).
Контрольная работа по теме «Произведение многочленов»
Вариант 1
• 1. Выполните умножение:
а) (с + 2) (с - 3); б) (2а - 1) (За + 4); в) (5х - 2у) (4х - у); г) (а - 2) (а2 - 3а + 6).
• 2. Разложите на множители: а) а (а + 3) - 2 (а + 3); б) ах - ау + 5х - 5у.
3. Упростите выражение -0,1x (2х2 + 6) (5 - 4х2).
4. Представьте многочлен в виде произведения:
а) х2 - ху - 4х + 4у; б) ab - ас - bх + сх + с - 6.
5. Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 2 см, а с другой, соседней, - 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см2 меньше площади прямоугольника.
Контрольная работа по теме «Произведение многочленов»
Вариант 2
• 1. Выполните умножение: а) (а - 5) (а - 3); б) (5х + 4) (2х - 1);
в) (3р + 2с) (2р + 4с); г) (6 - 2) (b2 + 2b - 3).
• 2. Разложите на множители: а) х (х - у) + а (х - у); б) 2а - 2b + са - сb.
3. Упростите выражение 0,5х (4х2 - 1) (5х2 + 2).
4. Представьте многочлен в виде произведения:
а) 2а - ас - 2с + с2; 6) bx + by - х - у - ах - ау.
5. Бассейн имеет прямоугольную форму. Одна из его сторон на 6 м больше другой. Он окружен дорожкой, ширина которой 0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2.
Контрольная работа по теме «Формулы сокращенного умножения»
Вариант 1
• 1. Преобразуйте в многочлен:
а) (у - 4)2; б) (7х + а)2; в) (5с - 1) (5с + 1); г) (3а + 2b) (3а - 2b).
• 2. Упростите выражение (а - 9)2 - (81 + 2а).
• 3. Разложите на множители: а) х2 - 49; б) 25х2 - 10ху + у2.
4. Решите уравнение (2 - х)2 - х (х + 1,5) = 4.
5. Выполните действия: а) (у2 - 2а) (2а + у2); б) (3х2 + х)2; в) (2 + т)2 (2 - т)2.
6. Разложите на множители: а) 4х2y2 - 9а4; б) 25а2 - (а + 3)2; в) 27т3 + п3.
Контрольная работа по теме «Формулы сокращенного умножения»
Вариант 2
• 1. Преобразуйте в многочлен:
а) (3а + 4)2; б) (2х - b)2; в) (b + 3) (b - 3); г) (5у - 2х) (5у + 2х).
• 2. Упростите выражение (с + b) (с - b) - (5с2 - b2).
• 3. Разложите на множители: а) 25у2 - а2; б) с2 + 4bс + 4b2.
4. Решите уравнение 12 - (4 - х)2 = х (3 - х).
5. Выполните действия: а) (3х + у2) (3х - у2); б) (а3 - 6а)2; в) (а - х)2 (х + а)2.
6. Разложите на множители: а) 100а4 - 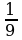 b2 ; б) 9х2 - (х - 1)2; в) х3 + у6.
b2 ; б) 9х2 - (х - 1)2; в) х3 + у6.
Контрольная работа по теме «Преобразование целых выражений»
Вариант 1
• 1. Упростите выражение:
а) (х - 3) (х - 7) - 2х (3х - 5); б) 4а (а - 2) - (а - 4)2; в) 2 (т + 1)2 - 4m.
• 2. Разложите на множители: а) х3 - 9х; б) -5а2 - 10аb - 5b2.
3. Упростите выражение (у2 - 2у)2 - у2(у + 3) (у - 3) + 2у (2у2 + 5).
4. Разложите на множители: а) 16х4 - 81; б) х2 - х - у2 - у.
5. Докажите, что выражение х2 - 4х + 9, при любых значениях х принимает положительные значения.
Контрольная работа по теме «Преобразование целых выражений»
Вариант 2
• 1. Упростите выражение:
а) 2х (х - 3) - 3х (х + 5); б) (а + 7) (а - 1) + (а - 3)2; в) 3 (у + 5)2 - 3у2.
• 2. Разложите на множители: а) с2 - 16с; б) 3а2 - 6аb + 3b2.
3. Упростите выражение (За - а2)2 - а2 (а - 2) (а + 2) + 2а (7 + 3а2).
4. Разложите на множители: а) 81а4 - 1; б) у2 - х2 - 6х - 9.
5. Докажите, что выражение -а2 + 4а - 9 может принимать лишь отрицательные значения.
Контрольная работа по теме «Системы линейных уравнений»
Вариант 1
• 1. Решите систему уравнений
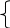 4х + у = 3,
4х + у = 3,
6х - 2у = 1.
•2. Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 р. и 3000 р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19000 р.?
| 3. Решите систему уравнений 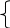 2 (3х + 2у) + 9 = 4х + 21, 2 (3х + 2у) + 9 = 4х + 21, 2х + 10 = 3 - (6х + 5у). | 4. Прямая у = кх + b проходит через точки А (3; 8) и В (-4; 1). Напишите уравнение этой прямой. |
5. Выясните, имеет ли решение система
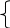 3x - 2y = 7,
3x - 2y = 7,
6х - 4y = 1.
Контрольная работа по теме «Системы линейных уравнений»
Вариант 2
• 1. Решите систему уравнений
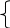 3х - у = 7,
3х - у = 7,
2х + 3у = 1.
• 2. Велосипедист ехал 2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его на шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе, и с какой по лесной дороге?
| 3. Решите систему уравнений  2(3х - у) - 5 = 2х - 3у, 2(3х - у) - 5 = 2х - 3у, 5 - (х - 2у) = 4у + 16. | 4. Прямая у = kx + b проходит через точки А (5; 0) и В (-2; 21). Напишите уравнение этой прямой. |
5. Выясните, имеет ли решения система и сколько:
 5х - у = 11,
5х - у = 11,
-10х + 2у = -22.
Итоговая контрольная работа по алгебре в 7 классе
Вариант 1
• 1. Упростите выражение: а) 3а2b • (-5а3b); б) (2х2у)3.
• 2. Решите уравнение 3х - 5 (2х + 1) = 3 (3 - 2х).
• 3. Разложите на множители: а) 2ху - 6y2; б) а3 - 4а.
• 4. Периметр треугольника ABC равен 50 см. Сторона АВ на 2 см больше стороны ВС, а сторона АС в 2 раза больше стороны ВС. Найдите стороны треугольника.
5. Докажите, что верно равенство
(а + с) (а - с) - b (2а - b) - (а - b + с) (а - b - с) = 0.
6. На графике функции у = 5х - 8 найдите точку, абсцисс которой противоположна ее ординате.
Итоговая контрольная работа по алгебре в 7 классе
Вариант 2
• 1. Упростите выражение: а) -2ху2 • Зх3у5; б) (-4аb3)2.
• 2. Решите уравнение 4 (1 - 5х) = 9 - 3 (6x - 5).
• 3. Разложите на множители: а) а2b - аb2; б) 9х - х3.
• 4. Турист прошел 50 км за 3 дня. Во второй день он прошел на 10 км меньше, чем в первый день, и на 5 км больше, чем в третий. Сколько километров проходил турист каждый день?
5. Докажите, что при любых значениях переменных верно равенство
(х - у) (х + у) - (а - х + у) (а - х - у) - а (2х - а) = 0.
6. На графике функции у = 3х + 8 найдите точку, абсцисса которой равна ее ординате.
| Рассмотрено на заседании МО | СОГЛАСОВАНО: | УТВЕРЖДАЮ: |
|
|
| Протокол № «___»______2014 г. | «___»______2014 г. | «___»______2014 г. |
|
|
| Руководитель МО | Зам.директора по УВР | Директор МБОУ «Школа № 5» |
|
|
| _____________Г.С. Зарипова | ______________ С.Е.Каминская | _____________Т.В.Курбанова |
|
|
Календарно-тематическое планирование
Алгебра
на 2014-2015 учебный год
I полугодие
7-г класс
Составитель: Лебединская О.А.
г. Муравленко
Календарно-тематическое планирование уроков алгебры в 7-х классах
( 3 часа в неделю), 1 полугодие.
| № | Тема
| Количество часов | Практическая часть |
| Контрольные работы | Лабораторные работы | демонстрации |
| 1 | Повторение | 2 |
|
|
|
| 2 | Выражения, тождества, уравнения | 19 | 2 |
|
|
| 3 | Линейная функция | 13 | 1 |
|
|
| 4 | Степень с натуральным показателем и еесвойства | 11 | 1 |
|
|
| 7 | Неполная неделя в ноябре | 1 |
|
|
|
| Итого | 48 | 4 |
|
|
Календарно – тематическое планирование по алгебре
7 г класс ФГОС (3 часа в неделю, 1 полугодие - 48 часов).
1 полугодие - 48 часов. КР – 4.
| № п/п | Тема урока | Количество часов
| Класс/дата проведения | Тип урока | Предметные результаты | УУД
| Учебно- методическое обеспечение | Домашнее задание |
| 1-2 | Повторение | 2 |
| Комб.
| Умение применять свойства действий | Исследовательская деятельность. Смысловое чтение: оценка информации | таблицы |
|
|
| Глава 1. Выражения, тождества, уравнения | 19 |
|
|
|
|
| 3 | Числовые и алгебраические выражения. | 1 |
| Частично поисков Комб.. | Умение находить значение числового выражения, значение алгебраического выражения | Исследовательская деятельность. Смысловое чтение: оценка информации | Опорные конспекты учащихся, сборник задач | П.1,№2, 6(а-г), 15,18 |
| 4,5 | Выражения с переменными | 2 |
| Комб. | Умение «переводить» математические правила, законы в символическую форму | Мотивация к познанию через анализ и нравственно-этическую оценку | Сборник задач. Тетрадь с конспектами | П.2, №21,23.25, 30,45 |
| 6,7 | Сравнения значений выражений | 2 |
| Проблемн изложение. Поисковый | Умение сравнивать значения выражения, находя их. | Организация и осуществление сотрудничества: ретрансляция опыта, взаимообучение, ролевые игры. | Опорные конспекты учащихся | П.3,№ 49,51,53(а), 67,69 |
| 8,9 | Свойства действий над числами | 2 |
| Комб. | Знать и применять законы действий | Организация и осуществление сотрудничества: ретрансляция опыта, взаимообучение, ролевые игры. | Сборник задач. Тетрадь с конспектами | П.4, №72, 74, 79(а), 81,83 |
| 10, 11, | Тождества. Тождественные преобразования | 2 |
| Комб. Частично поисков. | Упрощать выражения, используя законы действий | Эмпирические исследования. | Опорные конспекты учащихся | П.5, №86,91,93, 109 |
| 12 | Контрольная работа № 1. «Выражения. Тождества» | 1 |
| Контроль знаний, умений
| Умение самостоятельно выбрать рациональный способ решения | Коррекция деятельности: рефлексия, оценивание, самоконтроль | Диф. Контрольно измерительные матер. | 1,2,3,4,5 |
| 13 | Анализ контрольной работы | 1 |
| Коррекция | Умение анализировать и корректировать работу | Исследовательская деятельность. Смысловое чтение: оценка информации | Опорные конспекты учащихся | №96,99,102,103,108 |
| 14 | Уравнения и его корни | 1 |
| Комб. Частично поисков | Умение определять корень уравнения | Исследовательская деятельность. Смысловое чтение: оценка информации | Опорные конспекты учащихся | П.6, № 113,115,117.125 |
| 15, 16 | Линейное уравнение | 2 |
| Проблемный. | Умение находить корень уравнения по алгоритму | Эмпирические исследования. | Сборник задач, тетрадь с конспектами | П.7,№ 131,133,137.140,142 |
| 17-20 | Решение задач с помощью уравнений | 4 |
| Комб поисковый. | Составлять алгоритм решения задач | Коррекция деятельности: рефлексия, оценивание, самоконтроль | Сборник задач, тетрадь с конспектами | П.8, №152,154, 159,166 |
| 21 | Контрольная работа № 2. «Уравнения» | 1 |
| Контроль знаний, умений
| Умение самостоятельно выбрать рациональный способ решения заданий. | Коррекция деятельности: рефлексия, оценивание, самоконтроль | Диф. Контрольно измерительные матер. | П.6-8 |
|
| Глава 2. Линейная функция13 |
|
|
|
|
|
| 22 | Что такое функция | 1 |
| Комб поисковый. | Строить по координатам различные фигуры | Исследовательская деятельность. Смысловое чтение: оценка информации | Сборник задач, тетрадь с конспектами | П.12,13, №259,262, 265,270 |
| 23, 24 | График функции | 2 |
| Комб. | Умение применять правила и строить график уравнения | Организация и осуществление сотрудничества: ретрансляция опыта, взаимообучение, ролевые игры. | Раздаточный материал | П.14, №286,288, 290,295 |
| 25- 27 | Линейная функция и её график | 3 |
| Проблемный | Составление алгоритмов и построение графика | Эмпирические исследования. | Иллюстрации на доске, таблицы | П.15, №304,306, 311,312,357 |
| 28-29 | Прямая пропорциональность и её график | 2 |
|
| Умение по графику составлять уравнение прямой | Мотивация к познанию через анализ и нравственно-этическую оценку | Сборник задач, тетрадь с конспектами | П.16,№ 320, 322, 324, 329, 334,337 |
| 30-33 | Взаимное расположение графиков линейных функций | 3 |
| Комб. | Умение работать по заданному алгоритму | Коррекция деятельности: рефлексия, оценивание, самоконтроль | Сборник задач, иллюстрации на доске | П. 17,№ 326, 369 |
| 34 | Контрольная работа № 3. «Линейная функция» | 1 |
| Контроль знаний, умений | Умение самостоятельно выбрать рациональный способ решения | Коррекция деятельности: рефлексия, оценивание, самоконтроль | Контрольно измерительные материалы | П.12-17 |
| 35 | Анализ контрольной работы | 1 |
| Оценка и коррекция знаний
| Владение навыками самоанализа заданий. | Исследовательская деятельность. Смысловое чтение: оценка информации | Диф. Контрольно измерительные матер. | №338, 371,372 |
|
| Глава 3. Степень с натуральным показателем и её свойства 13 |
|
|
|
|
|
| 36, 37 | Что такое степень с натуральным показателем | 2 |
| Комб. | Умение находить значения сложных выражений со степенями | Мотивация к познанию через анализ и нравственно-этическую оценку | Раздаточный материал | П.18, № 374, 376,380,400 |
| 38, 39 | Умножение и деление степеней | 2 |
| Комб. | Умение применять правила | Организация и осуществление сотрудничества: ретрансляция опыта, взаимообучение, ролевые игры. | Раздаточный материал | П.19,№ 404, 406, 416 |
| 40-41 | Свойства степени с натуральным показателем | 2 |
| Комб поисковый.
| Составление алгоритмов | Эмпирические исследования. | Иллюстрации на доске, таблицы | П.20, № 429,432,436, 437,453 |
| 42 | Контрольная работа № 4. «Линейная функция» | 1 |
| Контроль знаний, умений | Отражение в письменной форме результатов соей деятельности | Коррекция деятельности: рефлексия, оценивание, самоконтроль | КИМы |
|
| 43, 44 | Понятие одночлена. Стандартный вид одночлена | 2 |
| Комб. | Умение работать по заданному алгоритму | Организация и осуществление сотрудничества: ретрансляция опыта, взаимообучение, ролевые игры. | Сборник задач, иллюстрации на доске | П.21, № 458, 460,464,466 |
| 45-48 | Действия с одночленами | 4 |
| Комб. |
| Исследовательская деятельность. Смысловое чтение: оценка информации | Сборник задач, тетрадь с конспектами | П.22-23, № 477,474(а,б), 480,485,497,498 |






 и
и 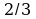 , у =
, у = 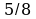 .
.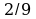 .
.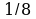 , у = -
, у = - 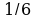 .
.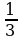 x = 12;
x = 12;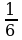 х = 18;
х = 18;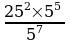 .
.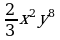 •
•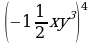 ; б) xn – 2 • x3 – n • x.
; б) xn – 2 • x3 – n • x.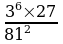 .
.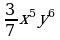 •
•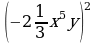 ; б) (an + 1 )2 : a 2n.
; б) (an + 1 )2 : a 2n.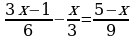 .
.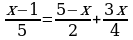 .
.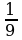 b2 ; б) 9х2 - (х - 1)2; в) х3 + у6.
b2 ; б) 9х2 - (х - 1)2; в) х3 + у6.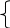 4х + у = 3,
4х + у = 3, 





















