Работа по теме фракталы

Слайд 2. Н Математика – древнейшая наука. Большинству людей казалось, что геометрия в природе ограничивается такими простыми фигурами, как линия, круг, многоугольник, сфера и т.д. Как оказалось многие природные системы настолько сложны, что использование только знакомых объектов обычной геометрии для их моделирования представляется безнадежным. Как, к примеру, построить модель горного хребта или кроны дерева в терминах геометрии?

Фракталы - подходящие средства для исследования поставленных вопросов. Нередко то, что мы видим в природе, интригует нас бесконечным повторением одного и того же узора, увеличенного или уменьшенного во сколько-то раз. Например, у дерева есть ветви. На этих ветвях есть ветки поменьше и т.д. Теоретически, элемент «разветвление» повторяется бесконечно много раз, становясь все меньше и меньше.

Слайд 3. С

Цель данной работы исследовать понятие фрактал и показать области его применения в человеческой деятельности.

Объектом исследования: фракталы в математике и в реальном мире

Предмет исследования: Фрактальная геометрия.

Гипотеза: строение человека, растительного мира и неживой природы едино с точки зрения фрактальной геометрии.

Слайд 4. С

Отцом современной фрактальной геометрии и слова фрактал является Бенуа Мандельброт. Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году. Фрактал — термин, означающий сложную геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.

Слайд 5-7. Н Алгебр Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых. Некоторые алгебраические фракталы поразительным образом напоминают изображения животных, растений и других биологических объектов, вследствие чего получили название биоморфов. Фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры, называются стохастическими. Известным представителем стохастических фракталов является плазма

Слайд 8.С Оказывается фракталы можно встретить повсеместно в живой и неживой природе.

Слайд 9-10.Н Фракталы находят все большее и большее применение в науке. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика.

Фрактальную геометрию используют для проектировании антенных устройств. Впервые это было применено американским инженером Натаном Коэном, который жил тогда в центре Бостона, где была запрещена установка на зданиях внешних антенн. Коэн вырезал из алюминиевой фольги фигуру в форме кривой Коха и затем наклеил ее на лист бумаги, а затем присоединил к приемнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы такой антенны не изучены до сих пор, это не помешало Коэну обосновать собственную компанию и наладить их серийный выпуск.

Слайд 11.С Рассмотрим методику «Драконовы ключи» созданную питерским художником Сергеем Рокомболем. Чаще всего её используются в арт-терапии. Данная методика состоит из серии рисунков основанных на фрактальной схеме матрицы. Дети одной из школ города Берлина после раскрашивания рисунков начали сами активно рисовать и сочинять сказки. Даже это уже значительный результат для развивающего ребенка. Практическая часть нашей работы состояла в том, что мы изучали простые геометрические фракталы и способы из построения.

Практическая часть нашей работы заключалась в том, мы что рассмотрели простейшие геометрические фракталы и способы их построения и попробовали создать свое собственное фрактальное изображения. Создали композицию из уже существующих фракталов и живописно разобрали данную работу. То, что у нас вышло можно посмотреть на картине «Фрактальная Вселенная».

Слайд 12. Н Данная работа является введением в мир фракталов. Мы рассмотрели только самую малую часть того, какие бывают фракталы, на основе каких принципов они строятся. Фракталы описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Но не следует забывать о том, что и фракталы — не более чем упрощенная модель реальности, которая не может претендовать на роль универсального ключа к описанию природы. В нашей работе приведены далеко не все области человеческих знаний, где нашла свое применение теория фракталов. Хотим только сказать, что со времени возникновения теории прошло не более трети века. Красота фракталов далеко не исчерпана и еще подарит нам немало шедевров - тех, которые услаждают глаз, и тех, которые доставляют истинное наслаждение разуму.

Министерство Образования и Науки Российской Федерации

Муниципальное общеобразовательное бюджетное учреждение

«Средняя общеобразовательная школа № 12»

Исследовательская работа

Фрактал — потрясающая красота математики в природе

Выполнили:

Митрюхина Софья Сергеевна,

Ласман Наталья Сергеевна,

учащиеся 8 "В" класса

Руководитель:

Глебов Алексей Юрьевич,

учитель математики

Минусинск, 2018

ВВЕДЕНИЕ 3

Глава I.История возникновения понятия фрактала. 6

Глава II.Виды фракталов в математике. 7

Геометрические. 7

Алгебраические. 9

Стохастические. 10

Глава III.Фракталы в живой и неживой природе. 11

Глава IV.Фракталы в других областях человеческой деятельности. 12

Глава V.Методика Драконовы ключи. 14

Глава VI. Практическая работа. 17

ЗАКЛЮЧЕНИЕ 21

СПИСОК ЛИТЕРАТУРЫ И ИСТОЧНИКОВ 22

Слово “фрактал” — это что-то, о чем много людей говорит в наши дни, от ученых до учеников средней школы. Оно появляется на обложках многих учебников математики, научных журналов и коробках с компьютерным программным обеспечением. Цветные изображения фракталов сегодня можно найти везде: от открыток, футболок до картинок на рабочем столе персонального компьютера. Итак, что это за цветные формы, которые мы видим вокруг?

Математика – древнейшая наука. Большинству людей казалось, что геометрия в природе ограничивается такими простыми фигурами, как линия, круг, многоугольник, сфера и т.д. Как оказалось многие природные системы настолько сложны, что использование только знакомых объектов обычной геометрии для их моделирования представляется безнадежным. Как, к примеру, построить модель горного хребта или кроны дерева в терминах геометрии? Как описать то многообразие биологических разнообразий, которое мы наблюдаем в мире растений и животных? Как представить всю сложность системы кровообращения, состоящей из множества капилляров и сосудов и доставляющей кровь к каждой клеточке человеческого тела? Представить строение легких и почек, напоминающие по структуре деревья с ветвистой кроной?

Фракталы - подходящие средства для исследования поставленных вопросов. Нередко то, что мы видим в природе, интригует нас бесконечным повторением одного и того же узора, увеличенного или уменьшенного во сколько-то раз. Например, у дерева есть ветви. На этих ветвях есть ветки поменьше и т.д. Теоретически, элемент «разветвление» повторяется бесконечно много раз, становясь все меньше и меньше. То же самое можно заметить, разглядывая фотографию горного рельефа. Попробуйте немного приблизить изображение горной гряды? вы снова увидите горы. Так проявляется характерное для фракталов свойство самоподобия.

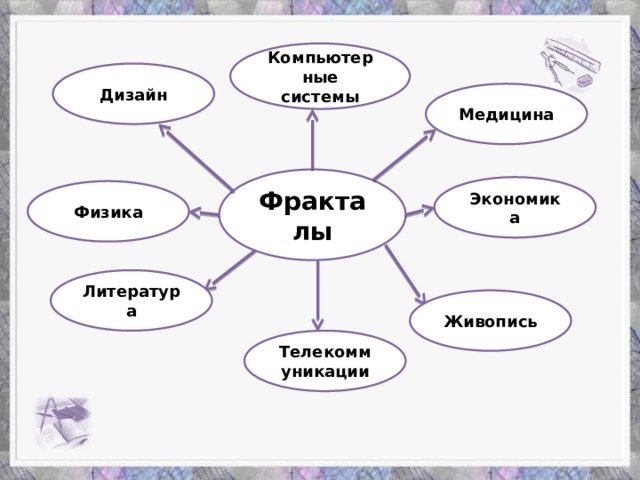
Изучение фракталов открывает замечательные возможности, как в исследовании бесконечного числа приложений, так и в области математики. Применение фракталов очень обширно! Ведь эти объекты настолько красивы, что их используют дизайнеры, художники, с помощью них в графике рисуются многие элементы деревья, облака, горы и т.д. А ведь фракталы используются даже как антенны во многих сотовых телефонах.

Для многих хаологов (ученых изучающих фракталы и хаос) – это не просто новая область познания, которая объединяет математику, теоретическую физику, искусство и компьютерные технологии — это революция. Это открытие нового типа геометрии, той геометрии, которая описывает мир вокруг нас и которую можно увидеть не только в учебниках, но и в природе и везде в безграничной вселенной.

Цель данной работы исследовать понятие фрактал и показать области его применения в человеческой деятельности.

Объектом исследования: фракталы в математике и в реальном мире

Предмет исследования: Фрактальная геометрия.

Гипотеза: строение человека, растительного мира и неживой природы едино с точки зрения фрактальной геометрии.

Задачи

• изучение научно-популярной литературы по данному вопросу, знакомство с научными гипотезами;

• знакомство с понятием и историей возникновения;

• Рассмотреть различные виды фракталов;

• нахождение подтверждения теории фрактальности окружающего мира;

• Рассмотреть возможности практического применения фрактала;

• Познакомиться с методикой Драконовы ключи и опробовать её;

• Придумать и создать собственный фрактал.

Методы исследования: аналитический, поисковый.

Практическая значимость: Данная работа может пригодится для расширения кругозора учащихся, формирования у них правильного представления о математике в современном мире. Материал работы может быть использован учителями для повышения мотивации к изучению предмета, как в урочной, так и внеурочной деятельности.

Почему геометрию часто называют холодной и сухой? Одна из причин заключается в ее неспособности описать форму облака, горы, дерева или берега моря. Облака - это не сферы, горы не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой. Открытие фракталов произвело революцию не только в геометрии, но и в физике, химии, биологии. Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке.

Отцом современной фрактальной геометрии и слова фрактал является Бенуа Мандельброт. Работая в IBM математическим аналитиком, он изучал шумы в электронных схемах, которые невозможно было описать с помощью статистики. Постепенно сопоставив факты, он пришел к открытию нового направления в математике - фрактальной геометрии.

Что же такое фрактал. Сам Мандельброт вывел слово fractal от латинского слова fractus, что означает разбитый (поделенный на части). Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения.

Фрактал — термин, означающий сложную геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы.

До появления фрактальной геометрии наука имела дело с системами, заключенными в трех пространственных измерениях. Благодаря Эйнштейну стало понятно, что трехмерное пространство — только модель действительности, а не сама действительность. Фактически наш мир расположен в четырехмерном пространственно-временном континууме.
       Благодаря Мандельброту стало понятно, как выглядит четырехмерное пространство, образно выражаясь, фрактальное лицо Хаоса. Бенуа Мандельброт обнаружил, что четвертое измерение включает в себя не только первые три измерения, но и интервалы между ними.

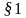Геометрические.

История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX веке. Фракталы этого класса — самые наглядные, потому что в них сразу видна самоподобность.

Фракталы этого типа строятся поэтапно. Сначала изображается основа. Затем некоторые части основы заменяются на фрагмент. На каждом следующем этапе части уже построенной фигуры, аналогичные замененным частям основы, вновь заменяются на фрагмент, взятый в подходящем масштабе. Всякий раз масштаб уменьшается. Когда изменения становятся визуально незаметными, считают, что построенная фигура хорошо приближает фрактал и дает представление о его форме. Для получения самого фрактала нужно бесконечное число этапов. Меняя основу и фрагмент, можно получить много разных геометрических фракталов.

Геометрические фракталы хороши тем, что, с одной стороны, являются предметом достаточного серьезного научного изучения, а с другой стороны, их можно «увидеть» — даже человек, далекий от математики, найдет в них что-то для себя. Такое сочетание редко в современной математике, где все объекты задаются с помощью непонятных слов и символов. Оказывается, многие геометрические фракталы можно нарисовать буквально на листочке бумаги в клетку. Сразу оговоримся, что все получаемые изображения являются лишь конечными приближениями бесконечных по своей сути фракталов. Но всегда можно нарисовать такое приближение, что глаз не будет различать совсем мелкие детали и наше воображение сможет создать верную картину фрактала. Например, имея достаточно большой лист миллиметровой бумаги и запас свободного времени, можно вручную нарисовать такое точное приближение к ковру Серпинского, что с расстояния в несколько метров невооруженный глаз будет воспринимать его как настоящий фрактал. Компьютер позволит сэкономить время и бумагу и при этом еще увеличить точность рисования.

Ещё одним типичным примером геометрического фрактала является кривая Коха. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т.д… Предельная кривая и есть кривая Коха.

Если в качестве основы взять равносторонний треугольник, то получим треугольник Серпинского. Равносторонний треугольник   делится прямыми, параллельными его сторонам, на 4 равных равносторонних треугольника. Из треугольника удаляется центральный треугольник. Получается множество, состоящее из 3 оставшихся треугольников «первого ранга». Поступая точно так же с каждым из треугольников первого ранга, получим множество, состоящее из 9 равносторонних треугольников «второго ранга» и так далее.

Алгебраические.

Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых.

Первые исследования в этом направлении относятся к началу XX века и связаны с именами французских математиков Гастона Жюлиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный труд Жюлиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жюлиа — целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то что это работа прославила Жюлиа среди математиков того времени, о ней довольно быстро забыли.

В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей. Благодаря иллюстрациям, полученным при помощи компьютера, и историческим байкам, которыми автор умело, разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике. Их успех среди нематематиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения. Когда персональные компьютеры стали достаточно мощными то появилось даже целое направление в искусстве — фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой теме.

Интересный факт, некоторые алгебраические фракталы поразительным образом напоминают изображения животных, растений и других биологических объектов, вследствие чего получили название биоморфов.

Стохастические.

Кривая Коха, как бы ни была похожа на границу берега, не может выступать в качестве её модели из-за того, что она всюду одинакова, самоподобна, слишком «правильна». Все природные объекты создаются по капризу природы, в этом процессе всегда есть случайность. Фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры, называются стохастическими. Термин «стохастичность» происходит от греческого слова, обозначающего «предположение».

Известным представителем стохастических фракталов является плазма. Для её построения возьмём прямоугольник и для каждого его угла определим цвет. Далее находим центральные точки прямоугольника и его сторон, и раскрашиваем их в цвет, равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число, пропорциональное размеру разбиваемого прямоугольника. Прямоугольник разбиваем на 4 равных, к каждому из которых применяется та же процедура. Далее процесс повторяется. Чем больше случайное число — тем более «рваным» будет рисунок.

Если мы теперь скажем, что цвет точки — это высота над уровнем моря, то вместо плазмы получим горный массив. Именно на этом принципе моделируются горы в большинстве программ. С помощью алгоритма, похожего на плазму, строится карта высот, к ней применяются различные фильтры, накладывается текстура и т. д. Рандомизированный фрактал строится по обычному алгоритму, за исключением того, что при вычислении на каждой итерации добавляются случайные величины.

Фрактальная геометрия описывает весьма широкий класс природных процессов и явлений, и поэтому мы можем вслед за Б.Мандельбротом с полным правом говорить о фрактальной геометрии природы. Новые - фрактальные объекты обладают необычными свойствами. Длины, площади и объемы одних фракталов равны нулю, других - обращаются в бесконечность.

Природа зачастую создаёт удивительные и прекрасные фракталы, с идеальной геометрией и такой гармонией, что просто замираешь от восхищения

Одним из типичнейших представителем фрактального подводного мира является коралл. В природе известно свыше 3500 разновидностей кораллов, в палитре которых различают до 350 цветовых оттенков. В строении морской

раковины так же хорошо видна структура фрактала.

На первый взгляд человек не обладает выраженной фрактальной внешностью. Но стоит заглянуть внутрь – всё встаёт на свои места.

Кровеносная, дыхательная, нервная система, сетчатка глаза - вот только самый беглый список биологических фракталов, которые присутствуют в каждом человеке.

Растения, деревья и травы - обладают выраженной фрактальной формой, в отличие, например от животных. Кроме того, что фрактальную структуру имеет лист растения (прожилки), общее строение растений также фрактально.

Структуру фрактала хорошо просматривается в формах горных хребтов, сталактитов и сталагмитов, ну и конечно в кристаллах.

Возьмём, к примеру, снежинки. Эти кристаллики образуются, когда в облаке водяной пар превращается в лёд. По мере роста кристалликов возникают изящные, ажурные узоры.

Стохастические фракталы можно увидеть в границах географических объектов и береговых линий, форме облаков и разрядах молний.

Фракталы находят все большее и большее применение в науке. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Вот несколько примеров:

Одни из наиболее мощных приложений фракталов лежат в компьютерной графике. Это фрактальное сжатие изображений. Современная физика и механика только начинают изучать поведение фрактальных объектов.

Достоинства алгоритмов фрактального сжатия изображений - очень маленький размер упакованного файла и малое время восстановления картинки. Фрактально упакованные картинки можно масштабировать без появления пикселизации (плохого качества изображения – большими квадратами). Но процесс сжатия занимает продолжительное время и иногда длится часами. Алгоритм фрактальной упаковки с потерей качества позволяет задать степень сжатия, аналогично формату jpeg. В основе алгоритма лежит поиск больших кусков изображения подобных некоторым маленьким кусочкам. И в выходной файл записывается только какой кусочек какому подобен. При сжатии обычно используют квадратную сетку (кусочки - квадраты), что приводит к небольшой угловатости при восстановлении картинки, шестиугольная сетка лишена такого недостатка.

В физике фракталы применяются ещё шире. Например в физике твёрдых тел фрактальные алгоритмы позволяют точно описывать и предсказывать свойства твёрдых, пористых, губчатых тел, различных аэрогелей. Это помогает в создании новых материалов с необычными и полезными свойствами. Пример твёрдого тела - кристаллы.

Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к из фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных систем. При помощи фракталов также можно смоделировать языки пламени. Пористые материалы хорошо представляются в фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в нефтяной науке.

Также фрактальную геометрию используют для проектировании антенных устройств. Впервые это было применено американским инженером Натаном Коэном, который жил тогда в центре Бостона, где была запрещена установка на зданиях внешних антенн. Коэн вырезал из алюминиевой фольги фигуру в форме кривой Коха и затем наклеил ее на лист бумаги, а затем присоединил к приемнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы такой антенны не изучены до сих пор, это не помешало Коэну обосновать собственную компанию и наладить их серийный выпуск. В данный момент американская фирма “Fractal Antenna System”разработала антенну нового типа. Теперь можно отказаться от использования в мобильных телефонах торчащих наружных антенн. Так называемая фрактальная антенна располагается прямо на основной плате внутри аппарата.

Среди литературных произведений находят такие, которые обладают

текстуальной, структурной или семантической фрактальной природой. В текстуальных фракталах потенциально бесконечно повторяются элементы

текста:

Также существуют множество гипотез по поводу применения фракталов – например, лимфатическая и кровеносная системы, лёгкие и многое другое тоже имеют фрактальные свойства.

В человеческом организме множество фракталоподобных образований — в структуре кровеносных сосудов и различных протоков, а также в нервной системе. Физиологам еще предстоит лучше понять то, каким образом процессы развития приводят к возникновению фрактальных структур. В недалеком будущем благодаря изучению фракталов ученые, возможно, получат более тонкие методы анализа различных нарушений функций организма при старении, заболеваниях и употреблении токсичных лекарственных препаратов.

Фрактальная живопись – одно из направлений современного арта, популярное среди цифровых художников. Фрактальные картины необычно и завораживающе действуют на зрителя, рождая яркие пылающие образы. Сказочные абстракции создаются посредством скучных математическим формул, но воображение воспринимает их живыми.

Отдельно такого понятия, как «фрактальный дизайн», пока еще не существует, но совсем скоро и этот стиль уже обретет собственное название и прочные связи с остальными направлениями. А пока дизайнеры со всего мира только начали использовать в своих работах эти замечательные структуры, только недавно описанные видными математиками.

Рассмотрим методику «Драконовы ключи» созданную питерским художником Сергеем Рокомболем. Чаще всего её используются в арт-терапии.

Данная методика состоит из серии рисунков основанных на фрактальной схеме матрицы. Все рисунки  сконструированы таким образом, что взаимодействие с ними проявляет и активизирует разнообразные и разноуровневые скрытые творческие возможности человека; и чем активнее взаимодействие, тем интенсивнее активизируются скрытые творческие потенциалы.

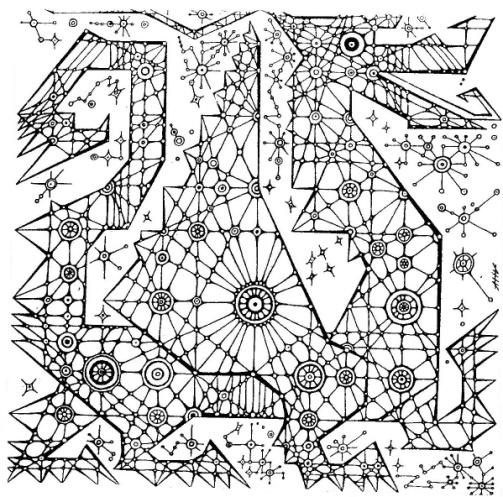
Первый эффект не заставит себя долго ждать, ребенку будет достаточно раскрасить один рисунок целиком, чтобы фоновая активность коры полушарий головного мозга повысилась. Это проявляется в потоке вопросов, фантазий, а иногда дети даже поют, играя и изучая рисунки.

Дети одной из школ города Берлина после раскрашивания рисунков начали сами активно рисовать и сочинять сказки. Даже это уже значительный результат для развивающего ребенка. Сами рисунки столь неординарны, что непременно вызывают интерес не только у детей; а попытки детского ума найти объяснение приводят к фантазированию, развитию воображения.

Второй значительный эффект – вслед за свободой, которую получает ребенок в выборе цветов, способов и последовательностей закрашивания у него появляются собственные творческие стремления и, как вы сможете сами убедиться, не только в сфере рисования. А креативность – это именно то качество, которое отличает развивающую личность.

Конструкция рисунков, заданная фрактальность их деталей разовьют мелкую моторику руки – это третий эффект. Благодаря столь особенному устройству иннервации кистей рук (нервные окончания напрямую принадлежит коре головного мозга, без переключений где-либо) этот эффект проявляется в дальнейшем как большая упорядоченность мыслительного аппарата ребенка. А, следовательно, ему будет гораздо проще справляться со школьными нагрузками.

Четвертый эффект – повышение способности к концентрации внимания и непосредственно следует из третьего. Развитие функций внимания одно из самых значительных последствий от взаимодействия с рисунками альбома «Драконовы Ключи», столь необходимых не только детям, но и многим взрослым людям – в сегодняшнем перегруженном информацией, мире.

Оригинальное исполнение рисунков, использование геометрии фракталов для создания сложных изображений, активизирует процесс развития способностей оперирования визуальными образами. Вследствие того, что 90% информации, получаемой извне, воспринимается человеком зрительно, повышение этой способности приводит в итоге к развитию памяти  у ребенка (в начале, конечно, зрительной, но затем и другие ее виды).

В рисунках среди прочих идей яркое выражение нашли идеи взаимодействия симметрий (их несколько) и асимметрии. Знакомство с этими явлениями как через парные рисунки в альбоме, так и через симметричные детали одного и того же рисунка приведет (и значимость этого шестого эффекта трудно переоценить) к активизации межполушарных связей в головном мозге. Полушария мозга ответственны за различные функции (в частности, кора полушарий) и в ситуации, когда одно из них перегружено, человек практически не способен на конструктивные способы разрешения проблем, в т.ч. задач познания. Именно в таком положении находятся 60% людей, обращающихся за помощью к психологу. Эта проблема исчерпывается, когда активность двух полушарий соотносится и используется рационально – к этому и приводит ребенка общение с симметриями и асимметриями в  рисунках – раскрасках альбома «Драконовы Ключи».

В процессе работы с рисунками альбома «Драконовы Ключи» организуется сознание, устанавливается гармоническое соотношение между правым и левым полушариями мозга, растет чувство ритма, сосредоточенность; укрепляется зрительная и моторная память, ассоциативное и образное мышление.

Высказанные соображения не голословны, они подкрепляются экспериментальной работой как зарубежных, так и наших психологов с детьми разного возраста. Руководитель исследовательской группы «Детская психиатрия», практический психолог Т.Чередникова в положительной рецензии на альбом «Драконовы Ключи» отмечает, что «большинство детей предпочитают картинки-раскраски из «Драконовых Ключей» другим раскраскам. В процессе работы у детей стимулируется психическая активность, пробуждается интерес и воображение, растет эмоциональный отклик, усиливается спонтанная речевая активность.

Использовать эту методику можно с разными целями. В первую очередь это диагностика интеллекта и эмоциональной сферы. Далее это развитие и коррекция тех же интеллектуальных и эмоциональных сфер, а также развитие и коррекция коммуникативных навыков. Ее можно использовать как в индивидуальной работе, так и в работе с группами, хорошо зарекомендовала она себя в работе с семьями для коррекции родительско-детских отношений.

Для диагностики интеллекта используется только изображение птицы. Процедура диагностики подробнейшим образом описана в монографии Чередниковой “Цветоструктурирование”.

Глава VI. Практическая работа.

Сначала остановимся на фракталах «Ожерелье», «Победа» и «Квадрат».

Первое – «Ожерелье» (рис.1). Инициатором данного фрактала является окружность. Эта окружность состоит из определенного числа таких же окружностей, но меньших размеров, а сама же она является одной из нескольких окружностей, представляющих собой такую же, но больших размеров. Так процесс образования бесконечен и его можно вести как в ту, так и в обратную сторону. Т.е. фигуру можно увеличивать, взяв всего одну маленькую дугу, а можно уменьшать, рассматривая построение ее из более мелких.

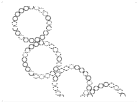
Рис. 1. Фрактал «Ожерелье»

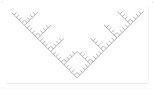
Второй фрактал – это «Победа» (рис.2). Такое название он получил потому, что внешне напоминает латинскую букву “V”, то есть “victory”-победа. Этот фрактал состоит из определенного числа маленьких “v”, составляющих одну большую “V”, причем в левой половине, которой маленькие ставятся так, чтобы их левые половины составляли одну прямую, правая часть строится так же. Каждая из этих “v” строится таким же образом и продолжается это до бесконечности.

Рис.2. Фрактал «Победа»

Третий фрактал – это «Квадрат» (рис. 3). Каждая из его сторон состоит из одного ряда ячеек, по форме представляющих квадраты, стороны которых также представляют ряды ячеек и т.д.

Рис.3.Фрактал «Квадрат»

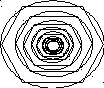
Фрактал был назван «Роза» (рис. 4), в силу внешнего сходства с данным цветком. Построение фрактала связано с построением ряда концентрических окружностей, радиус которых изменяется пропорционально заданному отношению (в данном случае Rм / Rб = ¾ = 0,75.). После чего в каждую окружность вписываются правильные шестиугольник, сторона которого равна радиусу описанной около него окружности.

Рис.4. Фрактал «Роза»

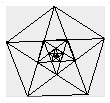Далее обратимся к правильному пятиугольнику, в котором проведём его диагонали. Затем в получившемся в при пересечении соответствующих отрезков пятиугольнике снова проведём диагонали. Продолжим данный процесс до бесконечности и получим фрактал «Пентаграмма» (рис. 5).

Рис. 5. Фрактал «Пентаграмма»

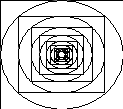
Рис. 6 фрактал «Черная дыра»

Теперь, когда мы поняли что такое фрактал и как его строить, мы попробовали создать свое собственное фрактальное изображения. Мы создали композицию из уже существующих фракталов и живописно разобрали данную работу. То, что у нас вышло можно посмотреть на рисунке 7 «Фрактальная Вселенная».

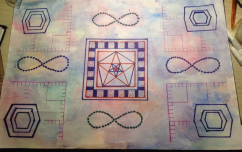
Рис. 7 «Фрактальная Вселенная»

Так же материал данной работы был использован нашим руководителем для подготовки и проведения открытого урока для конкурса «Лучший педагогический работник города Минусинска».

Данная работа является введением в мир фракталов. Мы рассмотрели только самую малую часть того, какие бывают фракталы, на основе каких принципов они строятся.

Изучая фракталы, анализируя проявления фракталов в окружающей нас действительности, а также в научных открытиях, связанных с существованием фракталов, мы обнаружили удивительно тесную связь математики и окружающим нас мира.

Фракталы описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Фракталы неисчерпаемы, как неисчерпаемы их приложения в науке, технике и искусстве. Но не следует забывать о том, что и фракталы — не более чем упрощенная модель реальности, которая не может претендовать на роль универсального ключа к описанию природы.

В нашей работе приведены далеко не все области человеческих знаний, где нашла свое применение теория фракталов. Хотим только сказать, что со времени возникновения теории прошло не более трети века, но за это время фракталы для многих исследователей стали внезапным ярким светом в ночи, которые озарил неведомые доселе факты и закономерности в конкретных областях данных. С помощью теории фракталов стали объяснять эволюцию галактик и развитие клетки, возникновение гор и образование облаков, движение цен на бирже и развитие общества и семьи. При подготовке данной работы нам было очень интересно находить применения ТЕОРИИ на ПРАКТИКЕ. Потому что очень часто возникает такое ощущение, что теоретические знания стоят в стороне от жизненной реальности.

Таким образом, концепция фракталов становится не только частью “чистой” науки, но и элементом общечеловеческой культуры. Фрактальная наука еще очень молода, и ей предстоит большое будущее. Красота фракталов далеко не исчерпана и еще подарит нам немало шедевров - тех, которые услаждают глаз, и тех, которые доставляют истинное наслаждение разуму.

1. Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. РХД 2001 г.

2. Витолин Д. Применение фракталов в машинной графике. // Computerworld-Россия.-1995

3. Мандельброт Б. Самоаффинные фрактальные множества, «Фракталы в физике». М.: Мир 1988 г.

4. Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.

5. Морозов А.Д. Введение в теорию фракталов. Н.Новгород: Изд-во Нижегород. ун-та 1999 г.

6. Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.

Интернет ресурсы

http://www.ghcube.com/fractals/determin.html

http://arbuz.uz/s_fractal.html

http://fractals.nsu.ru/fractals.chat.ru/

http://fractals.nsu.ru/animations.htm

http://www.cootey.com/fractals/index.html

http://fraktals.ucoz.ru/publ

http://ega-math.narod.ru/Nquant/Fractals.htm

http://sakva.narod.ru

http://rusnauka.narod.ru/lib/author/kosinov_n/12/

http://www.cnam.fr/fractals/

http://www.softlab.ntua.gr/mandel/

http://www.math.yale.edu/mandelbrot/

http://fractalworld.xaoc.ru/

http://fractbifur.narod.ru/html/index1.html

http://subscribe.ru/archive/job.education.maths/201005/06210524.html

Министерство Образования и Науки Российской Федерации

Муниципальное общеобразовательное бюджетное учреждение

«Средняя общеобразовательная школа № 12»

Фрактал — потрясающая красота математики в природе

Выполнили:

Митрюхина Софья Сергеевна,

Ласман Наталья Сергеевна,

учащиеся 8 "В" класса

Руководитель:

Глебов Алексей Юрьевич,

учитель математики

Минусинск, 2018

Объектом исследования: фракталы в математике и в реальном мире.

Предмет исследования: Фрактальная геометрия.

Задачи

• изучение научно-популярной литературы по данному вопросу, знакомство с научными гипотезами;
• знакомство с понятием и историей возникновения;
• Рассмотреть различные виды фракталов;
• нахождение подтверждения теории фрактальности окружающего мира;
• Рассмотреть возможности практического применения фрактала;
• Познакомиться с методикой Драконовы ключи и опробовать её;
• Придумать и создать собственный фрактал.

Французский и американский математик, создатель фрактальной геометрии. Лауреат премии Вольфа по физике.

20 ноября 1924 г. - 14 октября 2010 г.

Виды фракталов

Геометрические

Виды фракталов

Алгебраические

Виды фракталов

Стохастические

Фракталы вокруг нас

Компьютерные системы

Дизайн

Медицина

Фракталы

Экономика

Физика

Литература

Живопись

Телекоммуникации

Натан Коэн, американский инженер  

«Драконовы ключи»

Математика вся пронизана красотой и гармонией,

Только эту красоту надо увидеть.

Б. Мандельброт

Спасибо за внимание!