"Радианная мера угла"

Тема урока

Радианная мера угла

• Обучающие: дать понятие о радианном измерении углов,
• изучить связь между градусной и радианной мерами измерения углов,
• Развивающие:
• получение учащимися представлений о появлении тригонометрии как науки, о её практическом применении
• Воспитывающие: интерес к предмету,
• Аккуратности , взаимопомощи .

Цели урока:

Эпиграф к уроку :

• Незнающие пусть научатся , знающие – вспомнят еще раз…
• Античный афоризм.

• В древности люди следили за светилами и по этим наблюдениям вели календарь, рассчитывали сроки сева, время разлива рек; корабли на море, караваны на суше ориентировались в пути по звездам.
• Все это привело к потребности научиться вычислять стороны в треугольнике, две вершины которого находятся на земле, а третья представляется точкой на звездном небе.
• Исходя из этой потребности и возникла наука – тригонометрия – наука, изучающая связи между сторонами в треугольнике.

Углом какой четверти является угол?

225 0 ; -50 0 ; -315 0

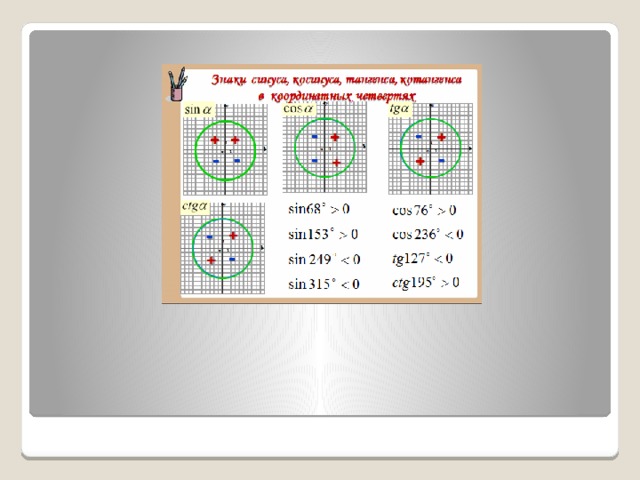
Какой знак имеют?

Sin 36 0 ; cos 108 0 ; tg 91 0 ; ctg 209 0

Sin 92 0 •cos 210 0

Sin 169 0 /cos 267 0

R

Радианная мера углов и дуг.

В математике и физике часто пользуются радианной мерой.

Построим угол МОР, такой что дуга МР, на которую он опирается, равна радиусу R окружности.

МР = R

М

R

180 0

360 0

=

1рад

=

p

p

2

1 радиан

p

=

Р

3

, 1459…

R

запиши

О

1рад. 57 0 17’

Запишите:

МР 57 0 17’ =1рад.

МОР 57 0 17’ = 1рад.

Определение

• Углом в один радиан называют центральный угол, которому соответствует длина дуги, равная длине радиуса окружности .

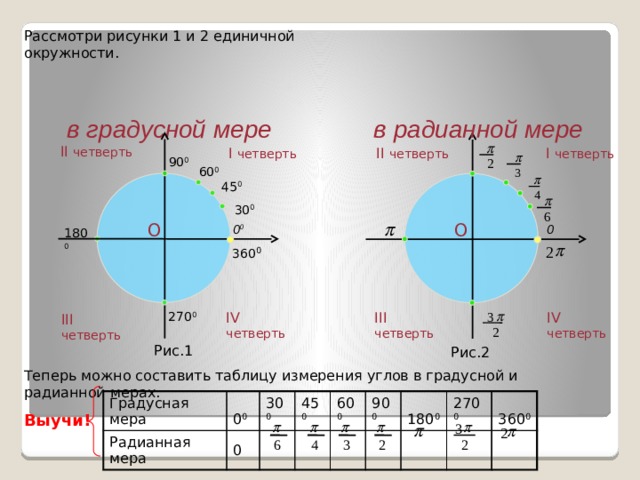
Рассмотри рисунки 1 и 2 единичной окружности.

в градусной мере

в радианной мере

p

II четверть

I четверть

I четверть

II четверть

p

90 0

2

60 0

3

p

45 0

4

p

30 0

6

О

О

p

0 0

0

180 0

p

360 0

2

IV четверть

270 0

IV четверть

III четверть

p

III четверть

3

2

Рис.1

Рис.2

Теперь можно составить таблицу измерения углов в градусной и радианной мерах.

Градусная мера

Радианная мера

0 0

0

30 0

45 0

60 0

90 0

180 0

270 0

360 0

Выучи!

p

p

p

p

p

3

p

p

2

3

4

6

2

2

Переход от радианной меры углов к градусной и от градусной к радианной

Переход от радианной меры углов к градусной

Выразим в градусах 4,5 рад.

Так как ,

то

Переход от градусной меры углов к радианной

Найдём радианную меру угла72 °

Так как ,то

При записи радианной меры угла, обозначение «рад» часто опускают.

Например:

Градус

Радианы

∏∕ 3

45

105

135

2∏∕3

п/5

70

4п/5

Заполните таблицу:

Градусы

60

Радианы

45

п/3

105

п/4

120

7п/12

2∏∕3

135

36

3∏∕4

п/5

144

4п/5

70

7/18п

Проверка таблицы:

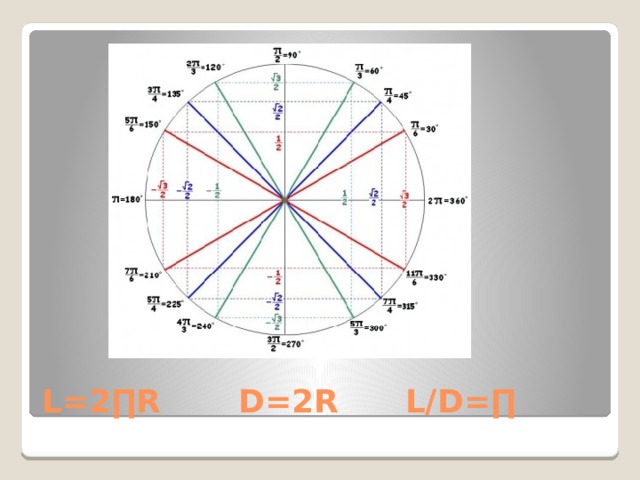
L=2∏R D=2R L/D=∏

• Перевести из радианной меры в градусную:
• 1 вариант 2 вариант
• ∏∕ 5 ∏∕18
• 5∏∕18 7∏∕10
• 11∏∕2 13∏∕4
• Перевести из градусной меры в радианную :
• 75 0 15 0 ; 9 0
• 10 0 ;144 0 720 0

Самостоятельная работа

• 1 вариант : 2 вариант
• 36 0 10 0
• 50 0 126 0
• 990 0 585 0

• 5∏∕12 ∏∕12
• ∏∕ 18 ∏∕20
• 4∏∕5 2∏

Проверьте свои знания :

• Домашнее задание :
• Страница 265 № 1 (4-8)
• № 2 (5-9)