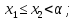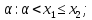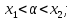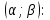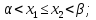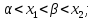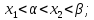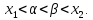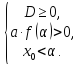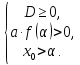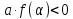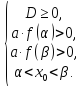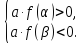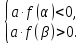Расположение нулей квадратичной функции на числовой прямой
Рассмотрим квадратный трехчлен 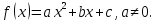
Пусть числа 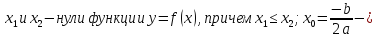 абсцисса вершины параболы, являющейся ее графиком.
абсцисса вершины параболы, являющейся ее графиком.
Рассмотрим задачи, в которых квадратный трехчлен задан явным образом, и требуется определить те значения параметра, при которых выполняется некоторое условие для расположения корней.
Перечислим основные условия:
оба корня меньше некоторого числа α: 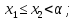
оба корня больше некоторого числа 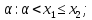
заданное число α лежит между корнями: 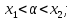
оба корня принадлежат заданному промежутку 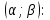
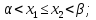
только меньший корень принадлежит промежутку 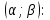
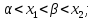
только больший корень принадлежит промежутку 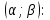
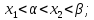
оба корня лежат по обе стороны от промежутка 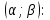
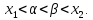
Рассматривать отдельно задачи, когда оба корня лежат справа или слева от промежутка, смысла не имеет, так как эти случаи в чистом виде соответствуют пунктам 1 и 2.
В таблице ниже приведены условия, необходимые и достаточные для выполнения перечисленных условий.
| Расположение нулей квадратичной функции на числовой прямой | Необходимые и достаточные условия |
|

x1 x2 α X |
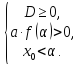
|
|

α x1 x2 X
|
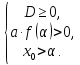
|
|

x1 α x2 X |
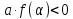
|
|

α x1 x2 β X |
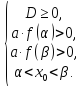
|
|

α x1 β x2 X |
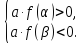
|
|

x1 α x2 β X |
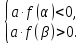
|
|

x1 α β x2 X |
|
Помочь запомнить все условия может очень простая «хитрость»: если мы знаем знак выражения  , то всегда можем определить, где лежит число α: между корнями или нет.
, то всегда можем определить, где лежит число α: между корнями или нет.
Объясняется это несложно. Если  , то «ветви» параболы направлены вверх. Тогда
, то «ветви» параболы направлены вверх. Тогда  , а вместе с ним и выражение
, а вместе с ним и выражение  , меньше нуля, когда число α находится между корнями трехчлена, и больше нуля, когда α не принадлежит интервалу
, меньше нуля, когда число α находится между корнями трехчлена, и больше нуля, когда α не принадлежит интервалу 
Если  то график квадратного трехчлена «растет» вниз. При этом значение
то график квадратного трехчлена «растет» вниз. При этом значение  , наоборот, больше нуля, когда число α находится между корнями. Однако выражение
, наоборот, больше нуля, когда число α находится между корнями. Однако выражение  снова отрицательно. Аналогично, это выражение положительно при α
снова отрицательно. Аналогично, это выражение положительно при α
Итак, если
Рассмотрим условия первого случая
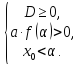
Неотрицательность дискриминанта дает существование корней, положительность выражения  соответствует тому, что
соответствует тому, что  , а последнее неравенство устанавливает расположение обоих корней слева от α, ведь абсцисса вершины параболы – середина отрезка [x1;x2] – находится слева.
, а последнее неравенство устанавливает расположение обоих корней слева от α, ведь абсцисса вершины параболы – середина отрезка [x1;x2] – находится слева.
Пример 1. Найти все значения параметра  , при которых корни уравнения имеют разные знаки.
, при которых корни уравнения имеют разные знаки.
Решение. Пусть f(x) =  = 0, , причем
= 0, , причем 
Условие того, что уравнение f(x) = 0 имеет корни разных знаков, равнозначно условию расположения числа 0 между нулями квадратичной функции y = f(x).
Необходимым и достаточным условием этого является следующее неравенство (см. третий случай в таблице): (a – 2) (a + 1) a – 2 – коэффициента при х2 квадратного трехчлена; f(0) = a + 1 – значение квадратного трехчлена при х = 0.
Решив неравенство (a – 2) (a + 1) a
Ответ: (– 1; 2).
Пример 2. Найти все значения параметра b, при которых корни уравнения меньше 1.
Решение.
Поскольку коэффициент при  содержит параметр, то нужно рассмотреть, когда он может быть равен нулю. При b = – 1 получаем корень х = – 1, который меньше числа 1.
содержит параметр, то нужно рассмотреть, когда он может быть равен нулю. При b = – 1 получаем корень х = – 1, который меньше числа 1.
Если b ≠ – 1, то выражение f(x) = является квадратным трехчленом, его корни обозначим как
является квадратным трехчленом, его корни обозначим как  , полагая
, полагая 
Абсцисса вершины параболы находится по формуле 
Значение квадратного трехчлена в точке х = 1:

Дискриминант:
Итак, должны выполняться три условия:
а) дискриминант больше или равен нулю;
б) выражение  положительно;
положительно;
в) абсцисса вершины параболы меньше числа 1.
Получаем систему неравенств:
Преобразуем её:
Изобразим решение каждого неравенства на рисунке:


 1
1



Таким образом, решением этой системы будут все значения  , принадлежащие интервалу (
, принадлежащие интервалу (
В итоге, корни уравнения меньше 1 при всех значениях [
Ответ: [
Пример 3. Найти все значения a, при которых корни уравнения
принадлежат отрезку [
Решение.
При a =  уравнение примет вид х = 0 и его решение принадлежит отрезку [
уравнение примет вид х = 0 и его решение принадлежит отрезку [
При a ≠  необходимые и достаточные условия того, что нули функции f(x) = принадлежат отрезку [
необходимые и достаточные условия того, что нули функции f(x) = принадлежат отрезку [ , задаются следующей системой:
, задаются следующей системой:
В этой системе: 
Итак,






 1
1








Ответ:  .
.
Задания для самостоятельного решения
При каких значениях параметра a корни уравнения
положительны?
Найти все значения b, при которых один из корней уравнения
больше 3, а другой меньше 3.
При каких m корни уравнения имеют разные знаки и каждый по модулю меньше 4?
При каких b корни уравнения по модулю меньше 1?
При каких значениях b оба корня уравнения
принадлежит интервалу (2; 5)?
При каких m все решения неравенства принадлежит отрезку [
Ответы:
1) [-5; -4]; 4) [ ;
;
2) ни при каких; 5) 
3) (-5,9; - 5,5); 6) (0; 1,5)







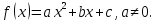
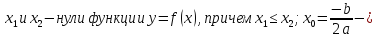 абсцисса вершины параболы, являющейся ее графиком.
абсцисса вершины параболы, являющейся ее графиком.